Probabilité de toucher la fève en découpant une galette des rois

Nous allons supposer que :

• la fève et la galette sont des disques de rayons $R_F$ et $R_G$,
• la galette est découpée en n parts égales selon des demi-droites d’origine le centre $O$ de la galette,
• le centre F de la fève est placé selon une loi de probabilité uniforme dans le disque de centre $O$ et de rayon $R_G - R_F$ (sinon, une partie de la fève serait à l’extérieur de la galette).

Soit $\lambda = \frac{R_{G}}{R_{F}}.$ Nous allons montrer que la probabilité cherchée est une fonction de λ et de n, soit $P(\lambda,n)$.

Il est à noter que les hypothèses précédentes (en gras) pourraient être relaxées. Néanmoins, elles ont l’avantage de permettre d’exprimer $P(\lambda, n)$ comme une fonction analytique de $\lambda$ et de $n$.

Il est clair que les hypothèses précédentes entraînent que $P(\lambda,n) = 1$ si $λ \leqslant 2$. Dans ce qui suit, nous allons donc supposer $n \geqslant 2$ (si $n=1$, il n’y a pas de découpe !) et $λ \geqslant 2$.

Nous allons considérer deux cas selon que F est à une distance R de O inférieure à $R_F$ (cas 1) ou supérieure à $R_F$ (cas 2).

Sans perte de généralité, on peut supposer que les angles des demi-droites sont égaux à $\frac{2k\pi}{n}, k \in \{ 0,1,...,n - 1\}$.

Cas 1 :

Dans ce cas, O appartient à la fève et donc le couteau va nécessairement toucher la fève puisque la découpe débute en O. Soit $p_1$ la probabilité que ce cas arrive. Comme la fève est placée uniformément dans le disque de centre O et de rayon $R_G - R_F$, on a :

Cas 2 :

La probabilité d’occurrence du cas 2 est :

Dans ce cas, soit α l’angle sous lequel la fève est vue depuis O, on a :

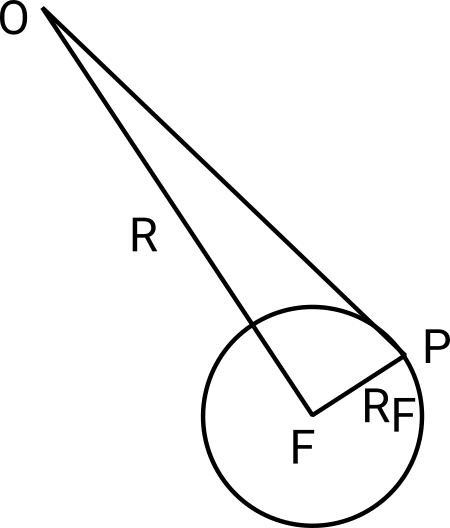
Le triangle OFP est rectangle en P, par conséquent on a:

Soient $(X, Y)$ et $(\Theta,R)$ les coordonnées cartésiennes et polaires de F:

$X = R \cos\Theta, Y = R\sin \Theta.$

Dans le cas 2, $F$ est uniformément réparti dans la couronne de centre $O$ et de rayons $R_F$ et $R_G - R_F$. La densité de probabilité de $(X, Y)$ est alors

Sachant qu’un élément d’aire $dx dy$ est égal à $rdrd\theta$, la densité de probabilité $p_{(\Theta, R)}$ de $(\Theta, R)$ s’écrit alors :

La densité de probabilité de $p_R$ de $R$ s’écrit alors :

D’après la Figure (1), la probabilité qu’une demi-droite D d’angle $\varphi$ touche la fève lorsque la fève est à une distance $R = r$ de O est égale à la probabilité que $\Theta$ appartienne, modulo 2π, au secteur angulaire $\lbrack \varphi - \frac{\alpha(r)}{2},\varphi + \frac{\alpha(r)}{2} \rbrack$, soit $\frac{\alpha(r)}{2\pi}$.

Par conséquent, la fève sera touchée lors de la découpe si, et seulement si, $\Theta$ appartient, modulo 2π, à l’un des secteurs angulaires $\{\left\lbrack \frac{2k\pi}{n} - \frac{\alpha(r)}{2},\frac{2k\pi}{n} + \frac{\alpha(r)}{2} \right\rbrack, k = 0,1,...,n - 1\}$. Si $R = r$, la probabilité d’intersection avec la fève est égale à :

La probabilité est égale à 1 si $r \leq \frac{R_{F}}{\sin(\pi/n)}$. Sachant que $r \leq R_{G} - R_{F},$ la probabilité d’intersection dans le cas 2 est donc égale à 1 si $\lambda \leq 1 + 1/\sin(\pi/ n).$ On a donc :

En particulier, (7) implique que la fève sera touchée asymptotiquement avec une probabilité 1 lorsque le nombre de parts est de plus en plus grand.

La probabilité de toucher la fève lors de la découpe, s’obtient en randomisant R dans (5) :

En reportant dans (5), on obtient :

Faisons le changement de variable $x = \frac{R_{F}}{r}$, on a alors :

Par conséquent, on peut écrire :

La première intégrale se calcule analytiquement :

Or, la probabilité cherchée s’écrit :

Tous calculs faits, on obtient :

où $\chi(\lambda)$ est égale à 1 si $\lambda \geqslant 1 + \cosec(\pi / n)$ et 0 sinon.

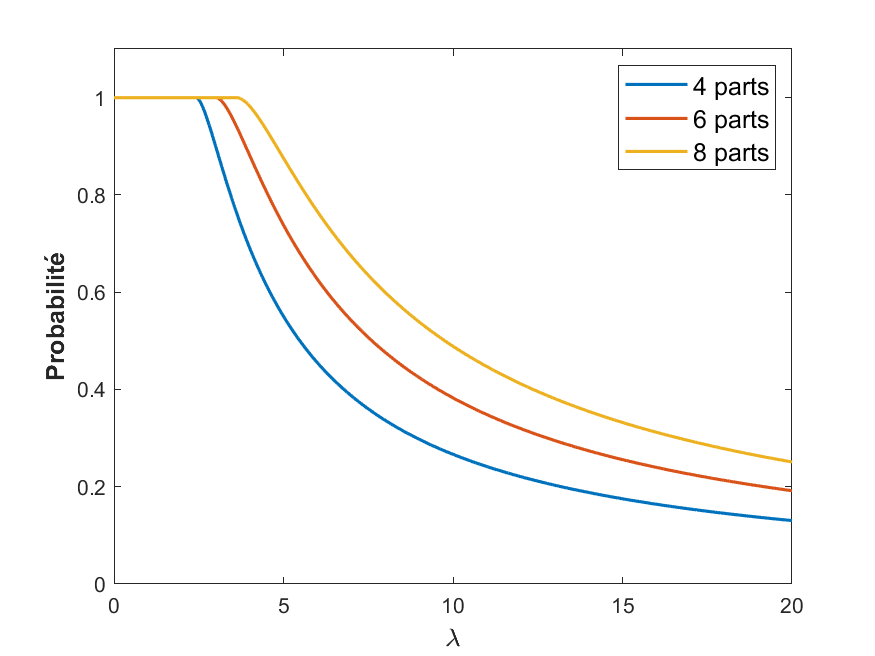
Les graphes de $P(λ, 4)$, $P(λ, 6)$ et $P(λ, 8)$ en fonction de $\lambda$ sont montrés Figure 2.

Ainsi, si la galette a un rayon 10 fois plus grand que la fève :