Bonjour,
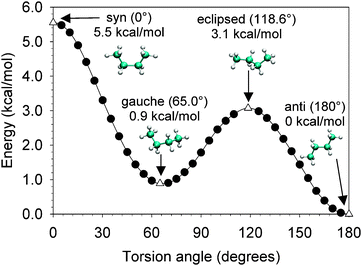
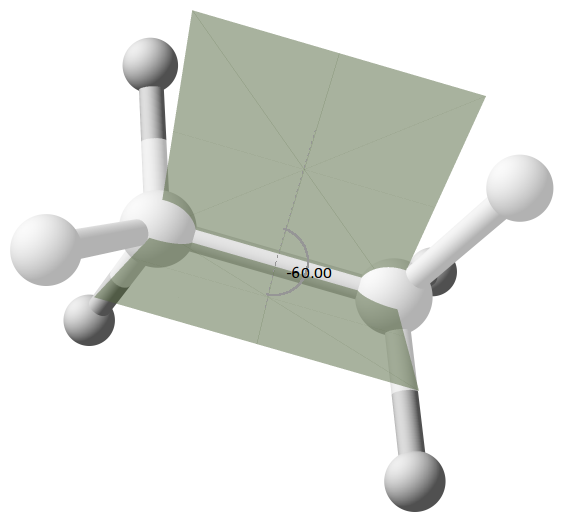
Je travaille en ce moment sur les stéréoisoméries (de configuration et conformation) et plus généralement sur les représentations spatiales de molécules organiques.
Cependant, j'ai l'impression, qu'à mon niveau du moins, ces notions, certes intéressantes, semblent un peu superficielles. Les idées de miroir plan et de la représentation de Cram sont bonnes, mais existe-il des applications minutieuses à la trigonométrie, pour étudier avec concision les transformations dans l'espace de ces molécules au cours de réactions chimiques, la chiralité, etc…?
D'après mes deux livres de chimie, recherches google : rien.
Merci.
+0
-0