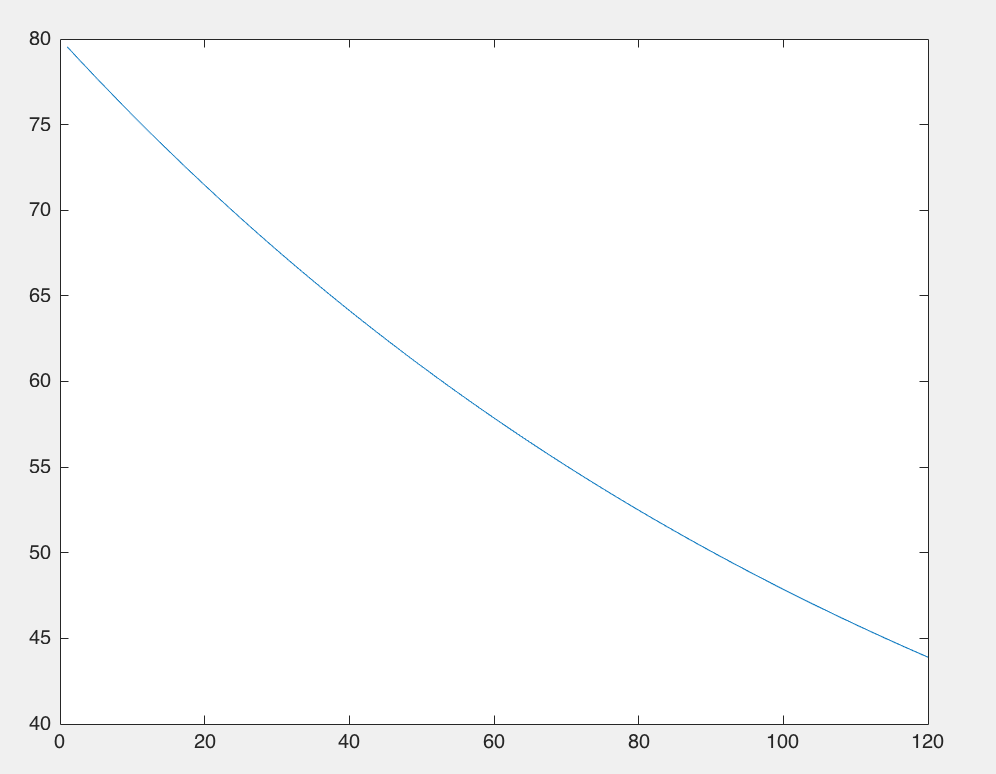
Voila plus en détails pour vous deux (et tous ceux qui lisent, sait on jamais que ce sujet passionne les foules…  ) le fond de ma pensée.
) le fond de ma pensée.
1) Méthode équation de chaleur avec condition aux limite "Température constante".
Ici on supposes que le milieu extérieur (l’air) peux évacuer AUTANT de chaleur que l’on veut (c’est la que je suis fondamentalement pas d’accord avec cette méthode, c’est une approximation bien trop extrême dans le cas d’une interface liquide(ou solide)-gaz, qui plus est quand il y a juste une convection naturel). Cela veux dire que le temps que va mettre à refroidir ton café dépend uniquement de la conductivité thermique de se dernier.
Cela veux dire egalement que si on étudie un très très bon conducteur comme du cuivre (ou un supraconducteur) il se refroidis quasiment instantanément (instamment pour un supraconducteur). Ce qui n’est pas réaliste.
L’erreur viens pour moi du fait que l’air ne peut pas emporter autant d’énergie que possible. L’air à une densité, une capacité calorifique et cela (entre autres) détermine la quantité d’énergie que peut dissiper l’air.
La conduction thermique à l’interface ce n’est rien d’autre que les atomes de gaz qui bombardent le liquide avec une certaine vitesse (dépendante de leur température) et qui rencontre les atomes du liquide qui on également une certain vitesse (dépendante de leur température), s’en suit une collision élastique, et, en moyenne les atomes de gaz repartent avec un peu plus d’énergie. Donc la température du gaz augmente, de la chaleur lui est transmise. Bien sur cette quantité de chaleur transmise va dépendre du nombre de collision (intuitivement on comprend bien que si on diminue la pression d’un facteur 1000 ton café va avoir plus de mal à refroidir).
C’est ce raisonnement qui m’a conduit à dire que si tu remplaces de l’air par du cuivre ça n’a rien avoir. Il me semble donc que tu avais mal compris l’argument @dri. Le cuivre ferai refroidir beaucoup plus vite le café.
2) Il faut donc utiliser une condition au limite mixte : le flux de température au niveau de la limite est proportionnel à la différence de température liquide-gaz et un facteur $h$ qui représente la capacité de l’air à évacuer de la chaleur du liquide. Ce coefficient $h$ est déterminé empiriquement il dépend de beaucoup de chose et notamment la convection. Mais on trouve aisément l’ordre de grandeur sur internet.
Au finale cette méthode d’écrit de manière complète ton système (dans le cadre des approximations pour la rendre solvable "analytiquement", cad que tu conclu que la solution est une somme de fourrier et que les coef ne sont pas déterminable analytiquement il faut donc un pc pour certaine étape, à la main c’est un coup à y passer des jours, c’est un truc de thésard du XIXeme siècle…). Mais une fois résolu tu as l’évolution de la température de ton liquide en chaque point de ta tasse.
Bien sur dans certain cas, si la conduction thermique de l’objet considéré (le café) est "beaucoup moins bonne" que le transfert à la limite, le coef $h$ devient négligeable et on peut utiliser un autre type de condition au limite (Neuman ou Dirichlet en fonction de la situation étudier, ou il eut être nécessaire de résoudre l’équation de chaleur dans les deux milieu, bref ça dépend des conditions) si ça simplifie les calculs.
Il ne me semble pas que la condition au limite soit un truc de "second ordre" dans ce cas (interface liquide-gaz) !
3) L’autre méthode que je propose plus haut est plus naïve, tu ne t’occupes en fais que de la surface d’échange, tu détermines quel quantité de chaleur par unité de temps peut la traverser (tu as donc également une coefficient $h$ mais qui n’est pas exactement le même que précédemment cependant il représente la même chose).
Ensuite il y a l’hypothèse très forte que la température dans ton café est homogène (!) et chaque watt qui traverse la surface fait légèrement augmenter la température T de ton café (de manière homogène donc). Tu n’as pas le détails et la répartition de la température dans ton café.
L’une des méthodes décrite fondamentale la dynamique du système et utilise les conditions aux limite pour intégrer la partie énergétique.
L’autre est juste une étude énergétique "grossière"
Au niveau des approximations :
Concernant les deux méthodes :
- on néglige l’interface café-tasse (on néglige donc un terme de perte)
Concernant la méthode d’équation de chaleur :
- on néglige la convection ( on néglige donc un terme de perte) Peut être il est compensable par un $\lambda$ effectif ?
Concernant la méthode du "bilan énergétique" :
- on néglige le gradient de température dans la tasse (qui la composition de la conduction dans l’eau + la convection). Du coup la différence de température utiliser pour déterminer l’échange d’énergie est sur estimé : on sur estime l’élévation de température.
La méthode du bilan énergétique à pour avantage qu’on peut facilement prendre en compte toute les interfaces (interface café-air, café-tasse et même tasse-air ce qui donne une système d’equa dif) sans compliquer le calcul.
Quand a la précision je rajouterai à ce qu’a dit @dri que à approximation égale (et avec une bonne gestion des conditions aux limites  ) la resolution de l’équation de chaleur donne des résultat plus précis.
Le problème c’est que l’équation de chaleur à 1D avec des approximation c’est "jouable", un bon exo de partiel quoi. Mais pour chaque approximation que tu enlèves tu rends le calcul plus compliqué et en pratique ce n’est solvable que numériquement.
L’avantage du bilan énergétique c’est que tu peux supprimer des approximations et toujours avoir un résultat rapidement en quelque lignes de calcul (exemple, prendre la tasse en compte)
) la resolution de l’équation de chaleur donne des résultat plus précis.
Le problème c’est que l’équation de chaleur à 1D avec des approximation c’est "jouable", un bon exo de partiel quoi. Mais pour chaque approximation que tu enlèves tu rends le calcul plus compliqué et en pratique ce n’est solvable que numériquement.
L’avantage du bilan énergétique c’est que tu peux supprimer des approximations et toujours avoir un résultat rapidement en quelque lignes de calcul (exemple, prendre la tasse en compte)
Bref ce sujet a piqué ma curiosité et je vais faire le calcul pour les différents cas afin de démêler le vrai du faux ^^.
(je suis dans le fond assez sur de ce que je dis, mais je peux me louper…)
edit:
et ya en effet un truc louche avec tes temperatures…
Il est à 25°C ou 29°C ton café ?
Et ta resolution est fausse ! Pour une bonne resolution garde $T_{ext}$ et $T_{ci}$ jusqu’à la fin.
Elle est fausse car tu ne monte pas bien à l’exponentielle.
exp(a+b) = ?
edit2 : "Vaël" 




 ).
). ) le fond de ma pensée.
) le fond de ma pensée.