Une égalité épatante

Détente mathématique

a marqué ce sujet comme résolu.

Bonjour à tous :-)

Vos journées sont longues ? Les transports fatigants ? Les nuits pas assez excitantes ?

Venez donc jouer un peu, venez faire des maths !

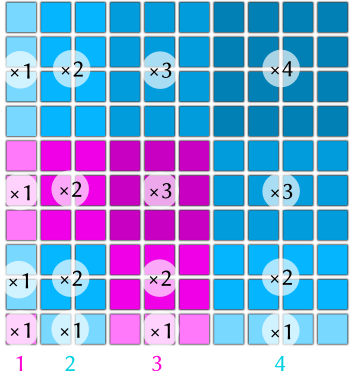
Pour cette première activité (grand public), je vous propose de démontrer (de la manière qui vous plaît la plus) l'égalité suivante :

$$ (1+2+\dots+n)^2 = 1^3+2^3+\dots + n^3 $$

où $n$ désigne un entier naturel.

Bien entendu, de multiples démonstrations sont possibles. Le but ici est que chacun puisse chercher dans son coin une solution. Et pour les meilleurs, en chercher une élégante et/ou étonnante (j'attends le premier qui utilisera les nombres de Betti).

Les règles pour jouer sont les suivantes :

  • placer dans un bloc secret sa réponse ;
  • faire un bloc (public) des pré-requis de la démonstration (par exemple sur l'identité $1+2+\dots+n = n(n+1)/2$ est un pré-requis) ;
  • écrire entièrement la démonstration.

Ensuite vient le moment des relectures, chacun pouvant relire et commenter qui il veut, en plaçant bien entendu dans un bloc secret ses commentaires (pour ne pas spoiler la personne qui recherche).

Amusez vous bien !

Voilà ma réponse :

Pré-requis :

$$ 1+2+\dots + n = \frac{n(n+1)}2 $$

La formule est vraie pour $n=1$ puisque $1^2=1^3$. Supposons la formule vraie au rang $n$ (pour $n\geq 1$), au rang $n+1$ on obtient

$$ [(1+2+\dots+n)+(n+1)]^2 = (1+2+\dots+n)^2 + 2 (n+1) ( 1+2+\dots+n) + (n+1)^2$$

on en déduit

$$ (1+2+\dots+n+(n+1))^2 = 1^3+2^3+\dots+n^3 + (n+1)\left(2\frac{n(n+1)}2 + (n+1)\right)$$

il s'en suit

$$ (1+2+\dots+n+(n+1))^2 = 1^3+2^3+\dots + n^3 + (n+1)(n^2+n+n+1) $$

et comme $n^2+2n+1= (n+1)^2$ on conclut que

$$ (1+2+\dots+n+(n+1))^2 = 1^3+2^3+\dots + n^3+(n+1)^3 $$

par récurrence, la formule est démontrée.

+9 -0

Bon, je vois pas grand chose d'original, et je pense d'après ton indice que j'ai la même démo que toi ^^'

Pré-requis :

$$ \sum_{i=1}^n i = \frac{n(n+1)}{2} $$

Montrons par récurrence sur $n \in \mathbb{N}$ que $(\sum_{i=1}^n i)^2 = \sum_{i=1}^n i^3$.

Initialisation : Pour $n=0$, on a :

$$ (\sum_{i=1}^n i)^2 = \sum_{i=1}^n i^3 = 0 $$

Hérédité : On considère $n \in \mathbb{N}$ et on suppose $(\sum_{i=1}^n i)^2 = \sum_{i=1}^n i^3$. On a :

$$ (\sum_{i=1}^{n+1} i)^2 = (\sum_{i=1}^n i)^2 + 2\times(n+1)\times(\sum_{i=1}^n i) + (n+1)^2 $$

Or :

$$ 2\times(n+1)\times(\sum_{i=1}^n i) + (n+1)^2 = 2\times(n+1)\times \frac{n(n+1)}{2} + (n+1)^2= (n+1)^3 $$

On a donc :

$$(\sum_{i=1}^{n+1} i)^2 = (\sum_{i=1}^n i^3) + (n+1)^3 = \sum_{i=1}^{n+1} i^3$$

La propriété est donc vraie pour tout $n \in \mathbb{N}$.

Edit: Bon je viens de lire ta démo et c'est la même tant pis je la laisse. :p

+2 -0

Bon je viens de lire ta démo et c'est la même tant pis je la laisse.

Il n'y a pas de problème à ça. Les mathématiques c'est faire des démonstrations. Quelles soient nouvelles ou non n'a absolument pas d'importance ici. Le but est simplement de se creuser un peu la tête :).

D'ailleurs si tu veux chercher une autre approche tu le peux, et même poster une nouvelle solution !

+0 -0

Petite piste pour ceux qui ne savent pas quoi chercher. Essayez de déterminer des conditions (nécessaires et/ou suffisantes) sur les entiers $n$ et $m$ afin que l'égalité reste vraie en remplaçant les exposants $2$ et $3$ par $p$ et $m$.

+0 -0

J'ai une démonstration avec une autre approche, qui part de l'idée qu'on a un carré et qu'il y a de la symétrie. Est-elle juste ?

Prérequis :

  • $\sum_{i=1}^n i = \frac{n(n+1)}{2}$
  • Manipulation de sommes
  • Matrice

On nomme $S$ le carré de la somme des $n$ premiers entiers naturels :

$$ S = \left(\sum_{i=1}^n i \right)^2 = \left(\sum_{i=1}^n i \right) \cdot \left(\sum_{j=1}^n j \right) = \sum_{i=1}^n \sum_{j=1}^n ij \, .$$

Soit une matrice carrée $M$ de taille $n$ dont les coefficients sont définis par $M(i,j) = ij$. Par définition, la somme des coefficients de $M$ est $S$. Dès lors, il est possible de les sommer comme on le souhaite, par exemple en séparant la diagonale, le triangle inférieur et le triangle supérieur :

$$ S = \sum_{i=1}^n i^2 + \sum_{i=1}^n \sum_{j=1}^{i-1} ij + \sum_{j=1}^n \sum_{i=1}^{j-1} ij \, .$$

Remarque. En toute rigueur, il faudrait $i = 2$ pour le deuxième terme et $j=2$ pour le troisième, mais ça force à séparer un morceau par la suite, et je ne crois pas que ça joue sur la validité de l'idée.

En jouant avec les indices muets, on montre que les deux derniers termes sont égaux, et donc :

$$ S = \sum_{i=1}^n i^2 + 2\sum_{i=1}^n \sum_{j=1}^{i-1} ij = \sum_{i=1}^n \left( i^2 + 2\sum_{j=1}^{i-1} ij \right) .$$

On peut calculer la somme interne :

$$ S = \sum_{i=1}^n \left( i^2 + 2i \frac{(i-1)i}{2} \right) .$$

En simplifiant, on obtient enfin :

$$ S = \sum_{i=1}^n i^3 .$$

La formule est démontrée.

+2 -0

J'ai tout de suite pensé à la récurrence. D'ailleurs selon moi ça devrait figurer parmi les prerequis, la somme des entiers de 1 à n pouvant être trouvée par récurrence alors que si on ignore le concept de la récurrence vos démonstrations deviennent inintelligibles.

J'ai trouvé une solution véritablement merveilleuse que cette zone de texte est trop étroite pour contenir (comprendre : je reviendrais poster avec autre chose qu'un smartphone ).

+0 -0

Allez, une variante de celle d'Holosmos/klafyvel, même prérequis

L'idée est de calculer $\left( \sum_i^n i \right)^2 - \left( \sum_i^{n-1} i \right)^2$, et de montrer que ça fait n³. Ensuite, en sommant tous les k³ pour k allant de 1 à n, les termes disparaissent deux à deux (vieille technique très courante et efficace en maths — comme quoi j'ai des restes :D ), et il ne reste que $\left( \sum_i^n i \right)^2$ - 0, d'où l'égalité recherchée.

$$ \left( \sum_i^n i \right)^2 - \left( \sum_i^{n-1} i \right)^2 = $$

$$ \left[ \frac{n (n+1)}{2} \right]^2 - \left[ \frac{(n-1) n)}{2} \right]^2 = $$

$$ \frac{n^2}{4} ( (n+1)^2 - (n-1)^2 ) = n^3 $$

C'est gagné.

Édit : légère confusion.

+2 -0

J'ai essayé de regarder un peu si on aurait pas des égalité de cette formes pour d'autres exposants que $2$ et $3$.

Le résultat m'étonne un peu, j'aurais imaginé une plus grande généralité. Il faudrait chercher à creuser sur des sommes partielles maintenant (commençant ailleurs qu'en $1$) pour voir ce que ça donnerait.

J'obtiens une réponse négative.

En effet, posons

$$ N = \sum_{k=1}^n = \frac{n(n+1)}{2} $$

il s'agit d'étudier

$$ (N+(n+1))^p = Q_m (n+1)^m $$

avec $Q_m = 1^m+\dots + n^m$. Cette égalité étant vraie pour $n=1$, il s'agit de montrer l'hérédité et donc que

$$ \sum_{k=0}^{p-1}\binom{p}{k}N^k(n+1)^{p-k} = (n+1)^m $$

on remplace $N^k$ par sa valeur et on obtient

$$ \sum_{k=0}^{p-1}\frac{n^k(n+1)^k}{2^k}(n+1)^{p-k} = (n+1)^m $$

et comme $(n+1)^k(n+1)^{p-k} = (n+1)^p$ cela nous ramène à :

$$ (n+1)^p\left(\sum_{k=0}^{p-1} \binom{p}{k}\frac{n^k}{2^k}\right) = (n+1)^m $$

mais on observe que la somme du premier membre est en fait égale à

$$ \left(1+\frac{n}2\right)^p - \frac{n^p}{2^p}. $$

Il s'en suit que l'égalité étudiée est équivalente à

$$ \frac{(n+2)^p - n^p}{2^p} = n^{m-p}. $$

En effet, le premier terme s'obtient en sortant un facteur $1/2^p$ du terme $(1+n/2)^p$ et le membre de droite fait sens puisqu'on peut bien évidemment supposer $m\geq p$.

Cette dernière égalité est équivalente à :

$$ \frac{1}{2^p}\left[\left(\sum_{k=0}^{p-1}\binom{p}{k}n^k\right) - n^p\right] = \sum_{k=0}^{m-p}\binom{m-p}{k}n^k. $$

Maintenant, supposons $p\neq 2$ puisque ce cas a déjà été étudié, et regardons le terme en $k=2$. En particulier, les coefficients devant $n^k$ pour chaque membre doivent être égaux, c'est-à-dire:

$$ \frac{1}{4}\binom{p}{2} = \binom{m-p}{2} $$

mais cela est équivalent à

$$ p(p-1) = 4(m-p)(m-p-1) $$

et cette équation d'inconnue $p$ du second degré a pour discriminant (je vous laisse vérifier, c'est inutilement long à écrire) :

$$ \Delta = -46m^2 - 56m + 4 $$

qui est évidemment négatif pour $m\geq 2$. Donc il n'y a pas de solution autre que $p=2, m=3$.

+0 -0
Banni

Version algébrique.

Edit : toujours même prérequis.

On remarque que $1 + 2 + \cdots + (n-1) + n + (n-1) + \cdots + 2 + 1 = n^2$. On a

$$(1+2+\cdots+n)^2 = 1(1) + 2(1+2+1) + \cdots + n(1+2+\cdots+n+\cdots+2+1)\text{,}$$
d'où l'égalité recherchée.

Visualisation associée.

J'avais fait ce dessin un autre jour, du coup je ne sais plus justifier pourquoi j'avais écrit « ×1 », « ×2 », etc. mais bref.
Visualisation d'une égalité
Par exemple, dans la zone violette correspondant à $3$, les sous-zones « ×1 » se couplent avec les sous-zones « ×2 » et se superposent à la sous-zone « ×3 » pour faire un bloc 3×3×3.

+3 -0
Banni

C'est vrai que j'ai pas justifié ma remarque.

J'avais mis comme « prérequis » le même que les autres propositions parce que c'est un peu la même idée. Il y a plusieurs manière de voir, l'une d'entre elles étant de coupler $k$ avec $n-k$, « à la Gauss » (le $n$ du milieu n'étant couplé avec aucun autre terme). On se retrouve avec $n$ fois le terme $n$ dans la somme.

+1 -0

Une petite remarque que l'on pourrait faire sur ce résultat, et qui me paraît pas nulle, est la suivante :

Pour rappel, la fonction $\zeta$ de Riemann a une expression analytique sur $\mathbf{C}$ avec un pôle d'ordre $1$ en $1$. En particulier,

$$ \zeta(-1) = -\frac1{12} \text{ et }\zeta(-3) = \frac1{120}. $$
On aurait pu s'attendre à ce que $\zeta(-1)^2 = \zeta(-3)$ mais ça n'est pas le cas. En particulier, ça donne une sorte de « trou » dans une théorie heuristique des séries divergentes puisqu'ici on a pas
$$ \left(\sum_{n\geq 1} n\right)^2 = \sum_{n\geq 1}n^3. $$

+0 -0

C'est peut-être un (le ?) prolongement mathématiquement correcte, mais à partir du moment où on dit que la somme infinie de nombre tous supérieur à 1 donne un résultat inférieur à 1, voire négatif, j'ai envie de dire, on n'est plus à ça près…

Stricto sensu, tu viens de démontrer que $\frac{-1}{12} = \frac{1}{120}$ avec la sommation étendue aux sommes infinis. :-° Pourquoi pas ?

+0 -0

C'est peut-être un (le ?) prolongement mathématiquement correcte

Le prolongement analytique d'une fonction est unique :-) (pour peu qu'on le fasse avec connexité).

mais à partir du moment où on dit que la somme infinie de nombre tous supérieur à 1 donne un résultat inférieur à 1, voire négatif, j'ai envie de dire, on n'est plus à ça près…

En fait c'est ce qu'il y a de plus critiquable. C'est une notation et plus une somme à proprement parler. Si on faisait le développement analytique on aurait certainement pas ça, puisque ça diverge grossièrement.

Mais certains apprécient ces notations et font des calculs heuristiques dessus, qui, de temps à autres tombent justes. Il y a des conditions à vérifier pour qu'une méthode de sommation marche bien, mais je reste sceptique.

Stricto sensu, tu viens de démontrer que $\frac{-1}{12} = \frac{1}{120}$ avec la sommation étendue aux sommes infinis. :-° Pourquoi pas ?

Gabbro

Non ! J'ai montré que

$$ 144 = 120, $$
et ça, c'est beau.

+3 -0

Non ! J'ai montré que

$$ 144 = 120, $$
et ça, c'est beau.

Holosmos

Exact, j'avais oublié le carrée.

Mais certains apprécient ces notations et font des calculs heuristiques dessus, qui, de temps à autres tombent justes.

Pas là, j'imagine. :D

+0 -0
Banni

Il s'en faut de peu pour que 144 égale 120 si l'on écrit lit le premier en base b et le deuxième en base b+1 : toujours 1 de différence. Ça aurait fonctionné avec 144 et 121, soit 12² et 11². Coïncidence ?

+1 -0

voici ma solution algébrique bourrine, peaufinée avec Mouton sur IRC, qui consiste à interpoler « bêtement » (mais pas tant que ça !) l’expression polynômiale des sommes de ce type, à partir desquelles on peut retrouver la formule cherchée. l’avantage, évidemment, est que ça se généralise directement. l’inconvénient, c’est que ça n’« explique » pas cette relation particulière… j’ai cherché une solution combinatoire / géométrique plus satisfaisante, mais ρττ a fait ça mieux que moi. :-)

prérequis :

  • algèbre linéaire de base
  • $\mathbf{R}[X]$

on pose $s^p_n = 1^p + 2^p + … + n^p$. pour $p$ fixé, on cherche une expression simple de $s^p_n$. on remarque que cette suite est également définie de façon unique par les relations (linéaires) :

$$ \begin{aligned} s^p_0 &= 0 \\ s^p_{n+1} &= s^p_n + (n+1)^p \end{aligned} $$

on définit sur $\mathbf{R}[X]$ l’opérateur linéaire $\Delta$ par $\Delta P = P[X] − P[X − 1]$. on voit rapidement que cette application fait chuter le degré d’exactement 1, donc que c’est une surjection $\mathbf{R}_{p+1}[X] \twoheadrightarrow \mathbf{R}_{p}[X]$, de noyau les polynômes constants.

on en déduit que le polynôme $X^p$ admet un antécédent $P$ de degré $p+1$, défini modulo le noyau de $\Delta$, donc modulo une constante. on peut donc prendre $P[0] = 0$. de sorte que :

$$ \begin{aligned} P[0] &= 0 \\ P[n+1] &= P[n] + (n+1)^p \end{aligned} $$

donc par unicité, $P[n] = s^p_n$.

on sait donc que $s^p$ est une fonction polynômiale de degré $p$, il nous suffit alors de calculer les $p+1$ premières valeurs et d’interpoler. :-)

…

en fait, on peut même interpoler intelligemment ! en effet, plutôt que la base de polynômes canonique, on peut considérer la base1 suivante :

$$ B^{(d)} = X(X+1)…(X+d−1) $$

il se trouve qu’on retrouve les propriétés de la dérivation usuelle !

$$ \Delta B^{(d)} = d × \Delta B^{(d−1)} $$

et donc si on écrit un polynôme dans cette base :

$$ P = p_0 + p_1 X + p_2 X(X+1) + … + p_d B^{(d)} $$

alors les coefficients sont donnés par la formule de Taylor :

$$ p_k = \frac {\Delta^k P[0]} {k!} $$

moi je trouve ça beau ^^

  1. de Newton ? ↩

+5 -0
Connectez-vous pour pouvoir poster un message.
Connexion

Pas encore membre ?

Créez un compte en une minute pour profiter pleinement de toutes les fonctionnalités de Zeste de Savoir. Ici, tout est gratuit et sans publicité.
Créer un compte