Hello les chimistes,
je viens demander un peu d'aide concernant les équilibres de complexation. En effet, j'ai deux concentrations données en Mn3+ (0.1 mol.L-1) et en C2O42- (0.15 mol.L-1) ; on mélange ces espèces, et je dois trouver les concentrations de tous les complexes et ions dans la solution.
J'ai les données suivantes :
- Mn3+ + Ox2- = [Mn(Ox)]+ ; Kf1 = 1010.6
- Mn(Ox)+ + Ox2- = [Mn(Ox)2]- ; Kf2 = 106.6
- Mn(Ox)2- + Ox2- = [Mn(Ox)3]3- ; Kf3 = 102.8
La première chose qui me vient, c'est de trouver quelle réaction est prépondérante. Seulement, j'ai 1.5 fois plus de ligands que de métal, donc est-ce que c'est la première réaction ou la seconde qui est majoritaire ?
Merci de votre aide par avance 
PS : ce sujet peut être utilisé pour toute question sur les équilibres de complexation !
+0
-0


 … Ceci dit, j'ai la réponse, du coup.
… Ceci dit, j'ai la réponse, du coup.
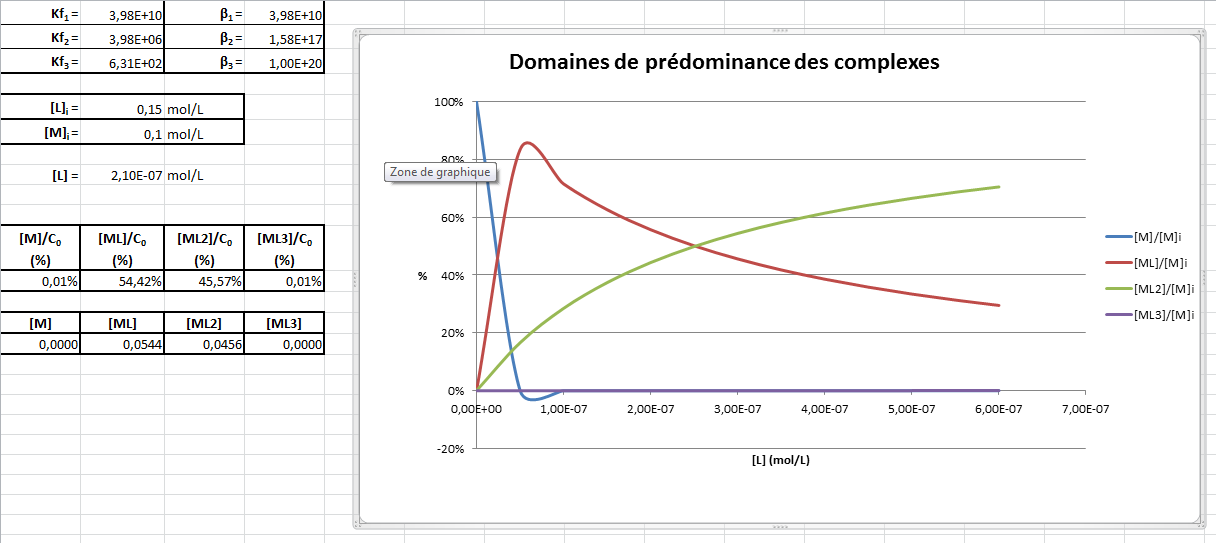 Attention : la courbe bleu passe en dessous de 0%, c'est dût au lissage de la courbe, les valeurs ne descendent jamais sous 0%, pareil pour l'espèce de bosse rouge, elle est trop prononcée à cause du lissage des courbes, il faudrait plus de points intermédiaires dans mes calculs.
Attention : la courbe bleu passe en dessous de 0%, c'est dût au lissage de la courbe, les valeurs ne descendent jamais sous 0%, pareil pour l'espèce de bosse rouge, elle est trop prononcée à cause du lissage des courbes, il faudrait plus de points intermédiaires dans mes calculs. Je vais juste utiliser la méthode la moins calculatoire étant donné que la calculatrice peut être interdite aux concours, d'autant qu'elle m'a l'air plus rapide.
Je vais juste utiliser la méthode la moins calculatoire étant donné que la calculatrice peut être interdite aux concours, d'autant qu'elle m'a l'air plus rapide.