Bonjour.
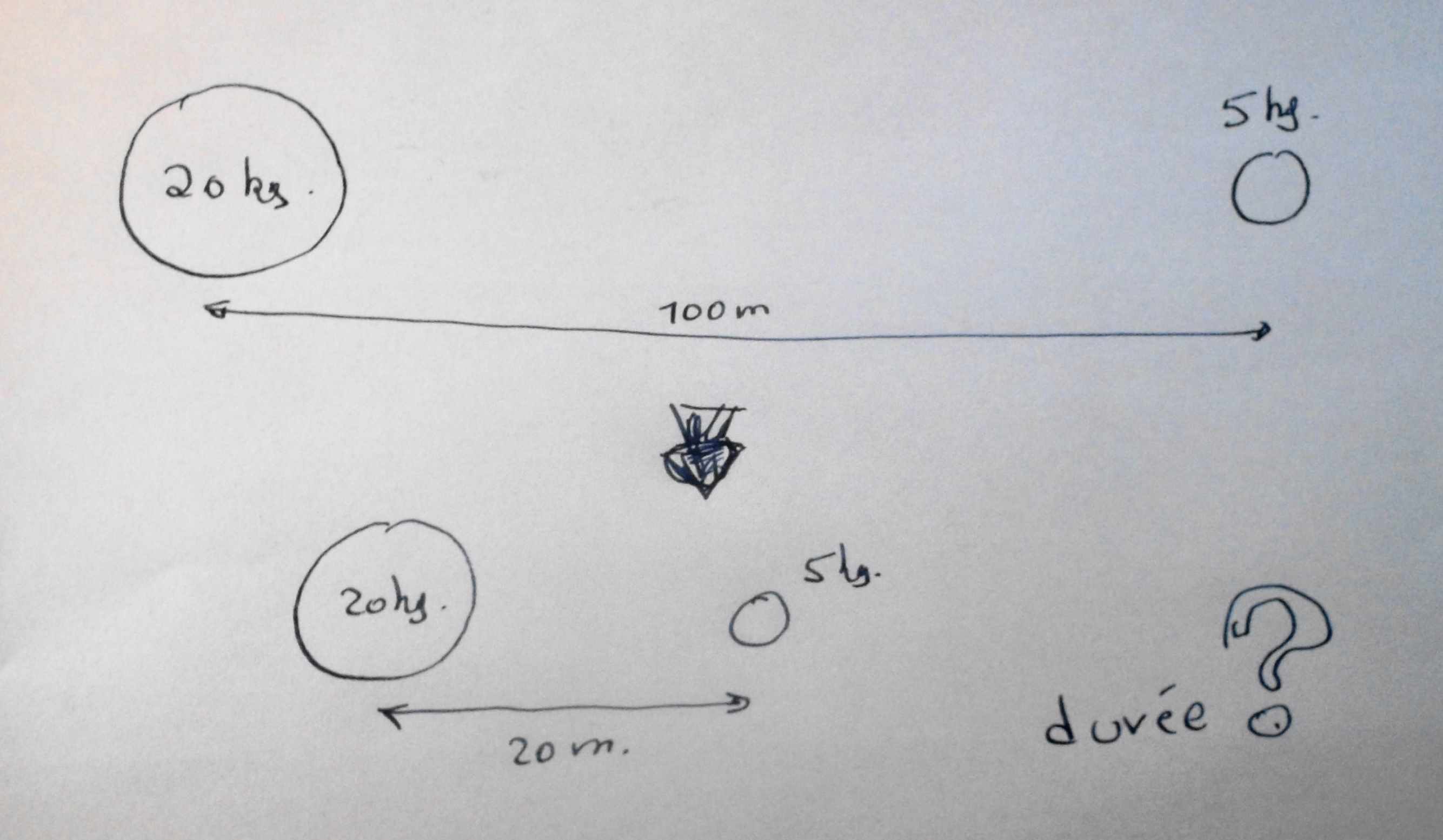
On a deux masses. 20 et 5 kg par exemple. Elles sont immobiles, distantes de 100 mètres. Toujours par exemple. Les distances sont mesurées entre centre de masse. On les lâchent. Et elles "tombent" l’une vers l’autre. Combien de temps mettent-elles pour arriver à 20 mètres l’une de l’autre?
Merci si vous répondez.
Dylan
Post scriptum. J’ai beaucoup cherché sur le net et dans les livres après une formule. Il me semble qu’elle n’existe pas. Sur d’autres forum, on m’a dit qu’il suffisait d’intégrer la (les) loi(s) de Newton. On m’a expliqué comment. Mais on ne m’a pas donné la solution… En désespoir de cause, j’ai utilisé la bonne vieille méthode. Par itération. J’ai donc divisé la distance parcourue par une des deux masses en 20 parties. Et j’ai calculé la vitesse de cette masse à l’entrée et à la sortie de chaque partie. Cà, on peut le faire. Puis en prenant la vitesse moyenne, j’ai calculé la durée pour chaque partie du trajet. Et donc la durée. Avec un tableur (Excel par exemple), c’est assez facile (quelques copier/coller de formule) et on peut diviser la distance en 1000, 2000.... Et les calculs se font toujours en une fraction de seconde. On peut même aisément calculer un temps minimum et un temps maximum. Il suffit de prendre pour chaque partie du trajet, soit la vitesse la plus grande ou la plus petite. C’est quand j’arrive aux conclusions que çà se gâte. Et que généralement, je me fais "virer" du forum. Si on prend une masse de 100 kg. Et qu’on la divise en deux parties. Les deux morceaux parcourent toujours "la même chute" dans le même temps. Quelque soit la division qui est faite. 1 et 99 kg; 50 et 50 kg. Galilée avait donc raison. Tous les corps tombent de la même façon sur terre. A la petite nuance près qu’ils doivent provenir de la terre. Par contre, si on prend une masse de 100 kg. Et qu’on y laisse tomber, dans les mêmes conditions de chute (hauteur) une masse de 1 ou 10 kg, la masse de 10 kg tombe plus vite (en moins de temps) que la masse de 1 kg. Aristote avait donc aussi raison. Les corps lourds tombent plus vite que les corps légers. Voilà, si quelqu’un voulait bien faire les calculs, çà me ferait vraiment plaisir.....


 .
.





 Je n’avais jamais remarqué.
Je n’avais jamais remarqué.
