Après une réception plutôt positive de mon premier billet de cette série de maths en images, je continue.
Aujourd’hui, c’est une illustration du théorème de Poincaré-Hopf. C’est l’un des résultat les plus merveilleux que je connaisse.
Le théorème de Poincaré-Hopf
Sans plus attendre, voici le dessin.
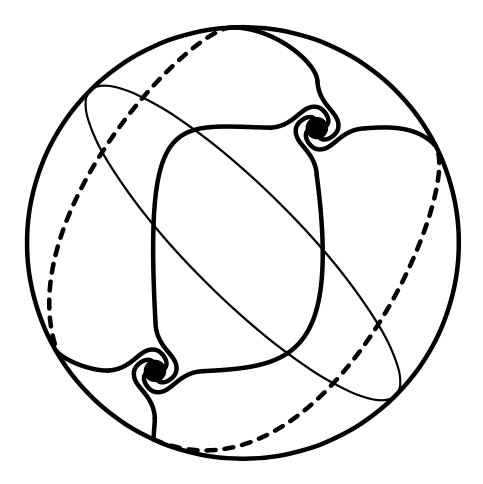
Que lire sur ce dessin ?
Prenez une sphère, et essayez d’imaginer les courants marins d’un océan imaginaire qui recouvrirait toute la sphère. Essayez de faire en sorte que sur tous les points de votre sphère imaginaire, le courant ne soit pas nul.
Est-ce possible ? Non. Peut-on en dire plus ? Oui, c’est le théorème de Poincaré-Hopf.
Quelque soit le courant que vous avez choisi, si vous regardez le lieu des zéros, vous pouvez compter le nombre de fois que l’on tourne autour du zéro. Dans le dessin ci-dessus, il y a deux zéros et à chaque fois on tourne $+1$. On obtient un nombre : $2$.
Ce nombre, et c’est ce qui fait la beauté de ce théorème, est toujours le même. C’est d’ailleurs un nombre qui intervient dans d’autres situations, c’est la caractéristique d’Euler-Poincaré.
Vous savez peut-être que si $G$ est un graphe planaire, alors la somme de ces sommets, moins ses arêtes, plus ses faces donne toujours le nombre $2$. Ce $2$ est encore la caractéristique d’Euler-Poincaré de la sphère sur laquelle vous avez dessiné votre graphe. N’est-ce pas merveilleux ?
En conclusion j’aimerais laisser le lien vers cet article d’Images des Maths. C’est l’un des plus beaux que je connaisse, c’est aussi l’un de ceux qui m’a donné envie de faire des maths.
Il aborde plus en détails ce qui est annoncé ici. C’est une très jolie ballade que je ne peux que vous recommander.



