J’aimais bien l’idée de donner des images liées à une activité scientifiques, comme proposée ici.
Vous avez probablement (si vous êtes abonné) pu apercevoir sur mon Twitter ce tweet où je présentais un dessin que j’avais réalisé pour mon mémoire (en cours d’écriture).
J’ai complété ce dessin, et je me suis dit que je pourrais le montrer ici.
Théorie de Morse
Prenez une forme géométrique (le terme correct est variété compacte), par exemple une surface. Cette surface vous pouvez essayer de la découper en fine lamelle. La théorie de Morse permet de reconstruire la forme initiale à partir de lamelle.
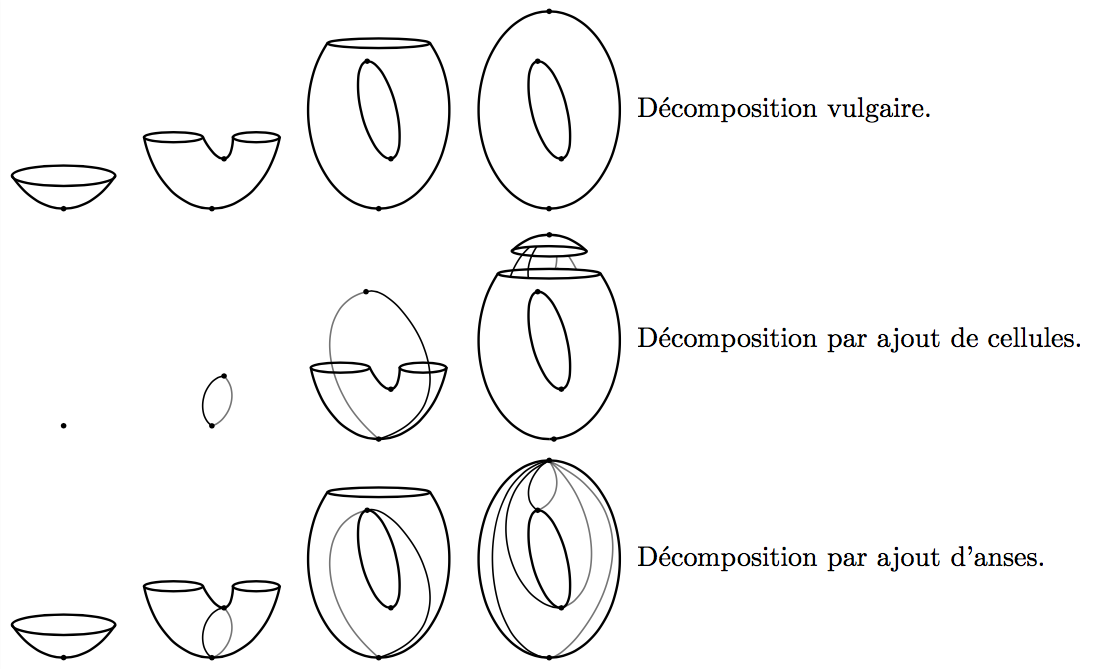
Les différentes décompositions représentent différentes finesses de la théorie de Morse. La première est simplement celle que l’on peut penser à la main, mais qui est difficile à argumenter : elle ne provient pas d’arguments rigoureux.
La deuxième est la première forme de la théorie de Morse et elle concerne la structure de CW-complexe. Chaque point critique, c’est-à-dire où une lamelle spéciale ne ressemble plus à la précédente, porte l’information : selon un entier que l’on appelle indice, on peut reconstruire la forme de notre objet à type d’homotopie près.
La troisième décomposition est plus intéressante parce qu’elle donne un type topologique : la forme obtenue à partir des lamelles est bien la même (topologiquement) que la forme initiale. Il faut pour cela compléter l’information précédente en ajoutant suffisamment de dimension pour avoir des anses.