Voici une petite correction de l’exercice 1 du bac de mathématiques de 2017, avec, bien entendu, des explications ! 
Le sujet ce trouve ici. Je vous invite à regarder les corrections de Holosmos aussi. 
[Partie A] Exponentielle, un incontournable
La fonction Exponentielle est un incontournable du bac.
Soit la fonction $h$ définie sur $\mathbf R^+ = [0, +\infty[$ par $h(x) = xe^{-x}$.
Question n°1
Il faut déterminer la limite en $+ \infty$ de la fonction $h$.
Par opération sur les limites, on aboutit à une forme indéterminée $0 \times (+ \infty)$
Commençons par remarquer que $e^{-x} = e^{0 - x} = \dfrac{e^0}{e^x} = \dfrac{1}{e^x}$. Dès lors, $h(x) = \dfrac{x}{e^x}$
A partir de là, on peut utiliser que $\dfrac{e^x}{x} \rightarrow + \infty$ avec $x$ (cas normalement vu en cours) et passer à l’inverse pour conclure que $\dfrac{x}{e^x} \rightarrow 0$ lorsque $x \rightarrow +\infty$.
Pour les plus curieux, voici deux preuves détaillée ici-bas.
Prérequis :
Montrons que $\displaystyle \lim_{x \to + \infty} \dfrac{ln(x)}{x} = 0$.
On sait que $ln(x) = \int_1^x \dfrac{1}{t} dt$ donc $\dfrac{ln(x)}{x} = \dfrac{1}{x} \int_1^x \dfrac{1}{t} dt$.
On remarque que $\forall t > 1, \sqrt{t} \leq t$, soit $\dfrac{1}{t} \leq \dfrac{1}{\sqrt{t}}$ puis $\int_1^x \dfrac{1}{t} dt \leq \int_1^x \dfrac{1}{\sqrt{t}} dt$ par les propriétés de l’intégrale.
Or, $\dfrac{1}{x} \int_1^x \dfrac{1}{\sqrt{t}} dt = \dfrac{1}{x} [2\sqrt{t}]_1^x = \dfrac{2\sqrt{x} - 2}{x} = \dfrac{2x^{\frac{1}{2}} + 2}{x} = \dfrac{x(2x^{-\frac{1}{2}} + \dfrac{2}{x})}{x} = 2\dfrac{1}{\sqrt{x}} + \dfrac{2}{x} \rightarrow 0$ lorsque $x \rightarrow +\infty$.
Donc, $0 < \dfrac{1}{x} \int_1^x \dfrac{1}{t} dt \leq \dfrac{1}{x} \int_1^x \dfrac{1}{\sqrt{t}} dt \iff 0 < \dfrac{ln(x)}{x} \leq 2\dfrac{1}{\sqrt{x}} + \dfrac{2}{x}$.
Cela permet de conclure $\dfrac{ln(x)}{x} \rightarrow 0$ lorsque $x$ tend vers l’infini positif, en utilisant le théorème des gendarmes.
Première preuve :
$\dfrac{e^x}{x} = exp(x - ln(x)) = exp(x(1 - \dfrac{ln(x)}{x}))$.
Quand $x \rightarrow +\infty$, $1 - \dfrac{ln(x)}{x} \rightarrow 1$ par opération sur les limites. S’ensuit $x(1 - \dfrac{ln(x)}{x}) \rightarrow +\infty$ donc $exp(x(1 - \dfrac{ln(x)}{x})) = \dfrac{e^x}{x} \rightarrow +\infty$.
En passant à l’inverse, on a bien $\dfrac{x}{e^x} \rightarrow 0$ lorsque $x$ tend vers l’infini positif.
Deuxième preuve (sans passer par $\dfrac{e^x}{x}$):
On pose $f = e^x$.
$\dfrac{x}{e^x} = \dfrac{ln(e^x)}{e^x} = \dfrac{ln(f(x))}{f(x)}$.
$f$ tend vers l’infini positif avec $x$, donc $\displaystyle \lim_{x \to +\infty} \dfrac{x}{e^x} = \displaystyle \lim_{x \to +\infty} \dfrac{ln(f(x))}{f(x)} = \displaystyle \lim_{x \to +\infty} \dfrac{ln(x)}{x} = 0$
Question n°2
On va étudier les variations de $h$ sur son domaine de définition.
On commence par dériver : $h'(x) = e^{-x} - xe^{-x} = e^{-x}(1 - x)$.
$x \mapsto e^x$ est strictement positive sur $\mathbf R^-$ donc notre dérivée est du signe de $1 - x$.
Il est alors facile de déterminer les variation de $h$ sur $[0, +\infty[$:
-
$x \mapsto 1 - x$ est positive sur $[0, 1[$ donc $h$ croît sur cet intervalle.
-
Elle s’annule en 1 puis change de signe, $h$ admet donc un maximum en $x = 1$ soit $max(h(\mathbf R^+)) = h(1) = e^{-1}$.
-
$h$ décroît évidement sur $]1, +\infty[$. N’oubliez pas d’indiquer sa limite!
Question n°3
On cherche à déterminer une primitive de h(x)…
a)
Vérifions que $\forall x \in \mathbf R^+, h(x) = e^{-x} - h'(x)$ :
$e^{-x} - h'(x) = e^{-x} - e^{-x} + xe^{-x} = xe^{-x} = h(x)$.
b)
Déterminons une primitive de $x \mapsto e^{-x}$ sur $\mathbf R^+$…
$(-e^{-x})' = -1 \times -e^{-x} = e^{-x}$
Donc $\int e^{-x} dx = -e^{-x}$.
c)
Dès lors, $\int h(x) dx = \int e^{-x} - h'(x) dx = -e^{-x} - xe^{-x} = -(x + 1)e^{-x}$.
[Partie B] Le logarithme népérien entre en jeu...
Soient $f$ et $g$ deux fonctions définies sur $\mathbf R^+$ par $f : x \mapsto xe^{-x} + \ln(x + 1)$ et $g : x \mapsto \ln(x + 1)$.
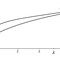
Voici maintenant les graphes de ces deux fonctions :

Question 1
$M (x, f(x))$ et $N (x, g(x))$ sont deux point respectivement situés sur $\mathcal C_f$ et $\mathcal C_g$ (ils ont la même abscisse).
On cherche à trouver la distance MN maximale.
Plaçons-nous dans le repère orthonormé $\mathcal R(O, \vec{i}, \vec{j})$ où $||\vec{i}|| = ||\vec{j}|| = 1$.
De ce fait, $\vec{MN} = (x - x)\vec{i} + (g(x) - f(x))\vec{j} = (xe^{-x} + \ln(x + 1) - \ln(x + 1))\vec{j} = (xe^{-x})\vec{j}$.
Ainsi, $||\vec{MN}|| = \sqrt{(xe^{-x})^2} = \sqrt{h(x)^2} = h(x)$ par stricte positivité de $h$ sur $\mathbf R^+$.
Or, comme nous l’avons vu dans la partie A, $h$ admet son maximum en $x = 1$.
Donc pour $M(1, e^{-1} + \ln(2))$ et $N(1, \ln(2))$, on a une distance maximale de $ e^{-1}$
Question 2
a)
Soit $\lambda \in \mathbf R^+$ et les droites d’équations $x = 0$ et $x = \lambda$.
On cherche à déterminer une expression de l’aire $\mathcal A_{\lambda}$ sous les deux courbes entre ces-deux droites.
$f$ et $g$ sont deux fonctions continues sur $\mathbf R^+$ (puisque dérivables) et telles que $f \geq g$. De ce fait, l’aire entre les deux courbes correspond à $\int_0^{\lambda} f(x)-g(x) dx$.
$\mathcal A_{\lambda} = \int_0^{\lambda} f(x) dx - \int_0^{\lambda} g(x) dx = \int_0^{\lambda} f(x) - g(x) dx$ par la linéarité de l’intégrale.
Donc $\mathcal A_{\lambda} = \int_0^{\lambda} xe^{-x} = [-(x + 1)e^{-x}]_0^{\lambda} = -e^{-\lambda} (\lambda + 1) + 1 = -\lambda e^{-\lambda} - e^{-\lambda} + 1 = -\dfrac{\lambda}{e^{\lambda}} - \dfrac{1}{e^{\lambda}} + 1 = 1 - \dfrac{\lambda + 1}{e^{\lambda}}$.
b)
On cherche à déterminer $\displaystyle \lim_{\lambda \to +\infty} 1 - \dfrac{\lambda + 1}{e^{\lambda}}$.
Pour ce faire, remarquons que $1 + \dfrac{\lambda + 1}{e^{\lambda}} = 1 - \dfrac{\lambda}{e^{\lambda}} + \dfrac{1}{e^{\lambda}}$ en divisant par $e^{\lambda}$ au numérateur et au dénominateur.
Ensuite, $\dfrac{\lambda}{e^{\lambda}} \rightarrow 0$ et $\dfrac{1}{e^{\lambda}} \rightarrow 0$ lorsque $x \rightarrow + \infty$.
Donc la limite est égale à 1.
Question 3
a)
Nous avons l’algorithme suivant :

On observe aisément que pour $S = 0,8$, l’algorithme nous ressort $\lambda = 3$.
b)
A quoi sert cet algorithme?
L’algorithme permet de déterminer le plus petit $λ$ tel que l’aire entre les courbes $\mathcal C_f$ et $\mathcal C_g$ et entre les droites d’équation $x = 0$ et $x = \lambda$ soit supérieure à S.
Prévenez moi s’il y a des pépins (c’est probable), n’ayant moi même pas trop réussi l’épreuve, je fais aussi cette correction à titre d’exercice.