Le but de cette première partie est, dans une première section, d’introduire rapidement en quoi consiste la preuve de programmes sans entrer dans les détails. Puis, dans une seconde section, de donner les quelques instructions nécessaires pour mettre en place Frama-C et les quelques prouveurs automatiques dont nous aurons besoin pendant le tutoriel.
Preuve de programmes
Assurer la conformité des logiciels
Assurer qu’un programme a un comportement conforme à celui que nous attendons est souvent une tâche difficile. Plus en amont encore, il est déjà complexe d’établir sur quel critère nous pouvons estimer que le programme « fonctionne ».
- Les débutants « essayent » simplement leurs programmes et estiment qu’ils fonctionnent s’ils ne plantent pas.
- Les codeurs un peu plus habitués établissent quelques jeux de tests dont ils connaissent les résultats et comparent les sorties de leurs programmes,
- La majorité des entreprises établissent des bases de tests conséquentes, couvrant un maximum de code, exécutés de manière systématique sur les codes de leurs bases. Certaines font du développement dirigé par le test.
- Les entreprises de domaines critiques, comme l’aérospatial, le ferroviaire ou l’armement, passent par des certifications leur demandant de répondre à des critères très stricts de codage et de couverture de code par les tests.
Et bien sûr, il existe tous les « entre-deux » dans cette liste.
Dans toutes ces manières de s’assurer qu’un programme fait ce qui est attendu, il y a un mot qui revient souvent : test. Nous essayons des entrées de programme dans le but d’isoler des cas qui poseraient problème. Nous fournissons des entrées estimées représentatives de l’utilisation réelle du programme (laissant souvent de côté les usages non prévus, qui sont souvent les plus dangereux) et nous nous assurons que les résultats attendus sont conformes. Mais nous ne pouvons pas tout tester. Nous ne pouvons pas essayer toutes les combinaisons de toutes les entrées possibles du programme. Toute la difficulté réside donc dans le fait de choisir les bons tests.
Le but de la preuve de programmes est de s’assurer que, quelle que soit l’entrée fournie au programme, si elle respecte la spécification, alors le programme fera ce qui est attendu. Cependant, comme nous ne pouvons pas tout essayer, nous allons établir formellement, mathématiquement, la preuve que le logiciel ne peut exhiber que les comportements qui sont spécifiés et que les erreurs d’exécution n’en font pas partie.
Une phrase très célèbre de Dijkstra exprime très clairement la différence entre test et preuve :
Program testing can be used to show the presence of bugs, but never to show their absence!
Le test de programme peut être utilisé pour montrer la présence de bugs mais jamais pour montrer leur absence.
Le Graal du logiciel sans bug
Dans chaque nouvelle à propos d’attaque sur des systèmes informatiques, ou des virus, ou des bugs provoquant des crashs, il y a toujours la remarque séculaire « le programme inviolable/incassable/sans bug n’existe pas ». Et il s’avère généralement que, bien qu’assez vraie, cette phrase est assez mal comprise.
Tout d’abord, nous ne précisons pas ce que nous entendons par « sans bug ». La création d’un logiciel fait toujours au moins intervenir deux étapes : la rédaction de ce qui est attendu sous la forme d’une spécification (souvent un cahier des charges) et la réalisation du logiciel répondant à cette spécification. À cela s’ajoute la spécification de notre langage de programmation qui nous définit la manière correcte de l’utiliser. Chacun de ces aspects peut donner lieu à l’introduction de bugs, que nous pouvons séparer en trois catégories :
- le programme n’est pas conforme, ou son comportement non défini, d’après la spécification du langage (par exemple, le programme accède en dehors d’un tableau pendant une recherche de l’indice de la valeur minimale) ;
- le programme n’est pas conforme à la spécification que nous en avons donné (par exemple, nous avons défini que le programme doit trouver l’indice de la valeur minimale d’un tableau, mais en fait il ne regarde pas sa dernière valeur à cause d’une erreur) ;
- la spécification ne reflète pas parfaitement « ce que nous voulons », et par conséquent, le programme non plus (par exemple, nous avons défini que le programme doit trouver l’indice de la valeur minimale d’un tableau, mais nous n’avons pas spécifié que s’il y en a plusieurs, il faut prendre la première, parce que cela me semblait trop évident, mais du coup ce n’est pas ce que fait le programme).
Chacune de ces catégories peut affecter la sûreté et/ou la sécurité de nos programmes, qui ne sont pas des notions tout à fait équivalentes. Pour donner une idée de la différence qui existe entre ces deux notions, nous pouvons dire que dans le cas de la sécurité, on suppose qu’il existe une entité capable d’attaquer (volontairement ou pas) le système, tandis que dans la sûreté, nous voulons juste vérifier que lorsqu’il est utilisé de manière conforme, le système se comporte correctement. Par conséquent, sans sûreté, nous ne pouvons pas avoir la sécurité1.
Tout au long de ce tutoriel, nous montrerons comment prouver que les implémentations de nos programmes ne contiennent pas de bugs correspondant aux deux premières catégories définies plus haut, à savoir qu’ils sont conformes :
- à la spécification de notre langage ;
- à la spécification de ce que nous attendons d’eux.
Mais quels sont les arguments de la preuve par rapport aux tests ? D’abord, la preuve est complète, elle n’oublie pas de cas s’ils sont présents dans la spécification (le test serait trop coûteux s’il était exhaustif). D’autre part, l’obligation de formaliser la spécification sous une forme logique demande de comprendre exactement le besoin auquel nous devons répondre.
Nous pourrions dire avec cynisme que la preuve nous montre finalement que l’implémentation « ne contient aucun bug de plus que la spécification », et donc que nous traitons pas la troisième catégorie de bugs que nous avons définie. Cependant, être sûr que le programme « ne contient aucun bug de plus que la spécification » est déjà un sacré pas en avant par rapport à savoir que le programme « ne contient pas beaucoup plus de bugs que la spécification », après tout cela représente deux catégories entières de bugs dont nous nous débarrassons, bugs qui peuvent déjà sévèrement compromettre la sûreté et la sécurité de nos programmes. Ensuite, il existe également des techniques pour traiter la troisième catégorie de bugs, en analysant les spécifications en quête d’erreurs ou d’insuffisance. Par exemple, les techniques de model checking - vérification de modèles - permettent de construire un modèle abstrait à partir d’une spécification et de produire un ensemble d’états accessibles du programme d’après le modèle. En caractérisant les états fautifs, nous sommes en mesure de déterminer si les états accessibles contiennent des états fautifs.
Un peu de contexte
En informatique, les méthodes dites formelles permettent de raisonner de manière rigoureuse, mathématique, à propos des programmes. Il existe un très large panel de méthodes formelles qui peuvent intervenir à tous les niveaux de la conception, l’implémentation, l’analyse et la validation des programmes ou de manière plus générale de tout système permettant le traitement de l’information.
Ici, nous nous intéresserons à la vérification de la conformité de nos programmes au comportement attendu. Nous utiliserons des outils capables d’analyser le code et de nous dire si oui, ou non, notre code correspond à ce que nous voulons exprimer. La technique que nous étudierons ici est une analyse statique, à opposer aux analyses dynamiques.
Le principe des analyses statiques est que nous n’exécuterons pas le programme pour nous assurer que son fonctionnement est correct, mais nous raisonnerons sur un modèle mathématique définissant l’ensemble des états qu’il peut atteindre. A l’inverse, les analyses dynamiques comme le test de programmes nécessitent d’exécuter le code analysé. Il existe également des analyses dynamiques et formelles, comme la génération automatique de tests ou encore des techniques de monitoring de code qui pourront, par exemple, instrumenter un code source afin de vérifier à l’exécution que les allocations et désallocation de mémoire sont faites de manière sûre.
Dans le cas des analyses statiques, le modèle utilisé est plus ou moins abstrait selon la technique employée, c’est donc une approximation des états possibles de notre programme. Plus l’approximation est précise, plus le modèle est concret, plus l’approximation est large, plus il est abstrait.
Pour illustrer la différence entre modèle concret et abstrait, prenons l’exemple d’un chronomètre simple. Une modélisation très abstraite du comportement de notre chronomètre est la suivante :

Nous avons bien une modélisation du comportement de notre chronomètre avec différents états qu’il peut atteindre en fonction des actions qu’il subit. Cependant, nous n’avons pas modélisé comment ces états sont réprésentés dans le programme (est-ce une énumération ? une position précise atteinte au sein du code ?), ni comment est modélisé le calcul du temps (une seule variable en secondes ? Plusieurs variables heures, minutes, secondes ?). Nous aurions donc bien du mal à spécifier des propriétés à propos de notre programme. Nous pouvons ajouter des informations :
- état arrêté à zéro : temps = 0s ;
- état en marche : temps > 0s ;
- état arrêté : temps > 0s.
Ce qui nous donne déjà un modèle plus concret mais qui est toujours insuffisant pour poser des questions intéressantes à propos de notre système comme : « est-il possible que dans l’état arrêté, le temps continue de s’écouler ? ». Car nous n’avons pas modélisé l’écoulement du temps par le chronomètre.
À l’inverse, avec le code source du programme, nous avons un modèle concret du chronomètre. Le code source exprime bien le comportement du chronomètre puisque c’est lui qui sert à produire l’exécutable. Mais ce n’est pas pour autant le plus concret ! Par exemple, l’exécutable en code machine obtenu à la fin de la compilation est un modèle encore plus concret de notre programme.
Plus un modèle est concret, plus il décrit précisément le comportement de notre programme. Le code source exprime le comportement plus précisément que notre diagramme, mais il est moins précis que le code de l’exécutable. Cependant, plus un modèle est précis, plus il est difficile d’avoir une vision globale du comportement qu’il définit. Notre diagramme est compréhensible en un coup d’oeil, le code demande un peu plus de temps, quant à l’exécutable … Toute personne qui a déjà ouvert par erreur un exécutable avec un éditeur de texte sait que ce n’est pas très agréable à lire dans son ensemble2.
Lorsque nous créons une abstraction d’un système, nous l’approximons, pour limiter la quantité d’information que nous avons à son sujet et faciliter notre raisonnement. Une des contraintes si nous voulons qu’une vérification soit correcte est bien sûr que nous ne devons jamais sous-approximer les comportements du programme : nous risquerions d’écarter un comportement qui contient une erreur. Inversement, si nous sur-approximons notre programme, nous ajoutons des exécutions qui ne peuvent pas arriver en réalité et si nous ajoutons trop d’exécutions inexistantes, nous pourrions ne plus être en mesure de prouver son bon fonctionnement dans le cas où certaines d’entre elles seraient fautives.
Dans le cas de l’outil que nous utiliserons, le modèle est plutôt concret. Chaque type d’instruction, chaque type de structure de contrôle d’un programme se voit attribuer une sémantique, une représentation de son comportement dans un monde purement logique, mathématique. Le cadre logique qui nous intéresse ici est la logique de Hoare adaptée pour le langage C et toutes ses subtilités (qui rendent donc le modèle final très concret).
Les triplets de Hoare
La logique de Hoare est une méthode de formalisation des programmes proposée par Tony Hoare en 1969 dans un article intitulé An Axiomatic Basis for Computer Programming (une fondation axiomatique pour la programmation des ordinateurs). Cette méthode définit :
- des axiomes, qui sont des propriétés que nous admettons, comme
« l’action “ne rien faire” ne change pas l’état du programme » ; - et des règles pour raisonner à propos des différentes possibilités de composition d’actions, par exemple « l’action “ne rien faire” puis “faire l’action A” est équivalent à “faire l’action A” ».
Le comportement d’un programme est défini par ce que nous appelons les triplets de Hoare :
où et sont des prédicats (c’est-à-dire des formules logiques) qui nous disent dans quel état se trouve la mémoire traitée par le programme. est un ensemble de commandes définissant un programme. Cette écriture nous dit « si nous sommes dans un état où est vrai, après exécution de et si termine, alors sera vrai pour le nouvel état du programme ». Dit autrement, est une précondition suffisante pour que nous amène à la postcondition . Par exemple, le triplet correspondant à l’action « ne rien faire » (skip) est le suivant :
skip
Quand nous ne faisons rien, la postcondition est la même que la précondition.
Tout au long de ce tutoriel, nous verrons la sémantique de diverses
constructions (blocs conditionnels, boucles, etc …) dans la logique de Hoare.
Nous n’allons donc pas tout de suite rentrer dans ces détails puisque nous en
aurons l’occasion plus tard. Il n’est pas nécessaire de mémoriser ces notions
ni même de comprendre toute la théorie derrière mais il est toujours utile
d’avoir au moins une vague idée du fonctionnement de l’outil que nous
utilisons.
Tout ceci nous donne les bases permettant de dire « voilà ce que fait cette action » mais ne nous donne pas encore de matériel pour mécaniser la preuve. L’outil que nous utiliserons repose sur la technique du calcul de plus faible précondition.
Calcul de plus faible précondition
Le calcul de plus faible précondition est une forme de sémantique de transformation de prédicats, proposée par Dijkstra en 1975 dans Guarded commands, non-determinacy and formal derivation of programs.
Cette phrase contient pas mal de mots méchants mais le concept est en fait très simple. Comme nous l’avons vu précédemment, la logique de Hoare donne des règles expliquant comment se comportent les actions d’un programme. Mais elle ne nous dit pas comment appliquer ces règles pour établir une preuve complète du programme.
Dijkstra reformule la logique de Hoare en expliquant comment, dans le triplet , l’instruction, ou le bloc d’instructions, transforme le prédicat , en . Cette forme est appelée « raisonnement vers l’avant » ou forward-reasoning. Nous calculons à partir d’une précondition et d’une ou plusieurs instructions, la plus forte postcondition que nous pouvons atteindre. Informellement, en considérant ce qui est reçu en entrée, nous calculons ce qui sera renvoyé au plus en sortie. Si la postcondition voulue est au plus aussi forte, alors nous avons prouvé qu’il n’y a pas de comportements non-voulus.
Par exemple :
int a = 2;
a = 4;
//postcondition calculée : a == 4
//postcondition voulue : 0 <= a <= 30
Pas de problème, 4 fait bien partie des valeurs acceptables pour a.
La forme qui nous intéresse, le calcul de plus faible précondition, fonctionne dans le sens inverse, nous parlons de « raisonnement vers l’arrière » ou backward-reasoning. À partir de la postcondition voulue et de l’instruction que nous traitons, nous déduisons la précondition minimale qui nous assure ce fonctionnement. Si notre précondition réelle est au moins aussi forte, c’est-à-dire, qu’elle implique la plus faible précondition, alors notre programme est valide.
Par exemple, si nous avons l’instruction (sous forme de triplet) :
a
Quelle est la précondition minimale pour que la postcondition soit respectée ? La règle nous dira que est a.
Nous n’allons pas nous étendre sur ces notions pour le moment, nous y reviendrons au cours du tutoriel pour comprendre ce que font les outils que nous utilisons. Et nos outils, parlons-en justement.
- Selon votre domaine d’activité, le terme sûreté peut avoir un sens très différent. Plus précisément, un système sûr serait un système qui ne doit jamais mettre la vie d’un humain en danger. Et donc dans ce cas, la situation est inverse : sans sécurité, nous ne pouvons pas avoir la sûreté. Dans ce tutoriel, nous nous plaçons bien dans le cas « sûreté = le programme ne présente pas de problème lorsqu’on l’utilise de manière conforme ».↩
- Il existe des analyses formelles cherchant à comprendre le fonctionnement des exécutables en code machine, par exemple pour comprendre ce que font des logiciels malveillants ou pour détecter des failles de sécurité introduites lors de la compilation.↩
Frama-C

Frama-C ? WP ?
Frama-C (pour FRAmework for Modular Analysis of C code) est une plate-forme dédiée à l’analyse de programmes C créée par le CEA List et Inria. Elle est basée sur une architecture modulaire permettant l’utilisation de divers plugins. Les plugins fournis par défaut comprennent diverses analyses statiques (sans exécution du code analysé), dynamiques (avec exécution du code), ou combinant les deux. Ces plugins peuvent collaborer ou non, soit en communiquant directement entre eux, soit en utilisant le langage de spécification fourni par Frama-C.
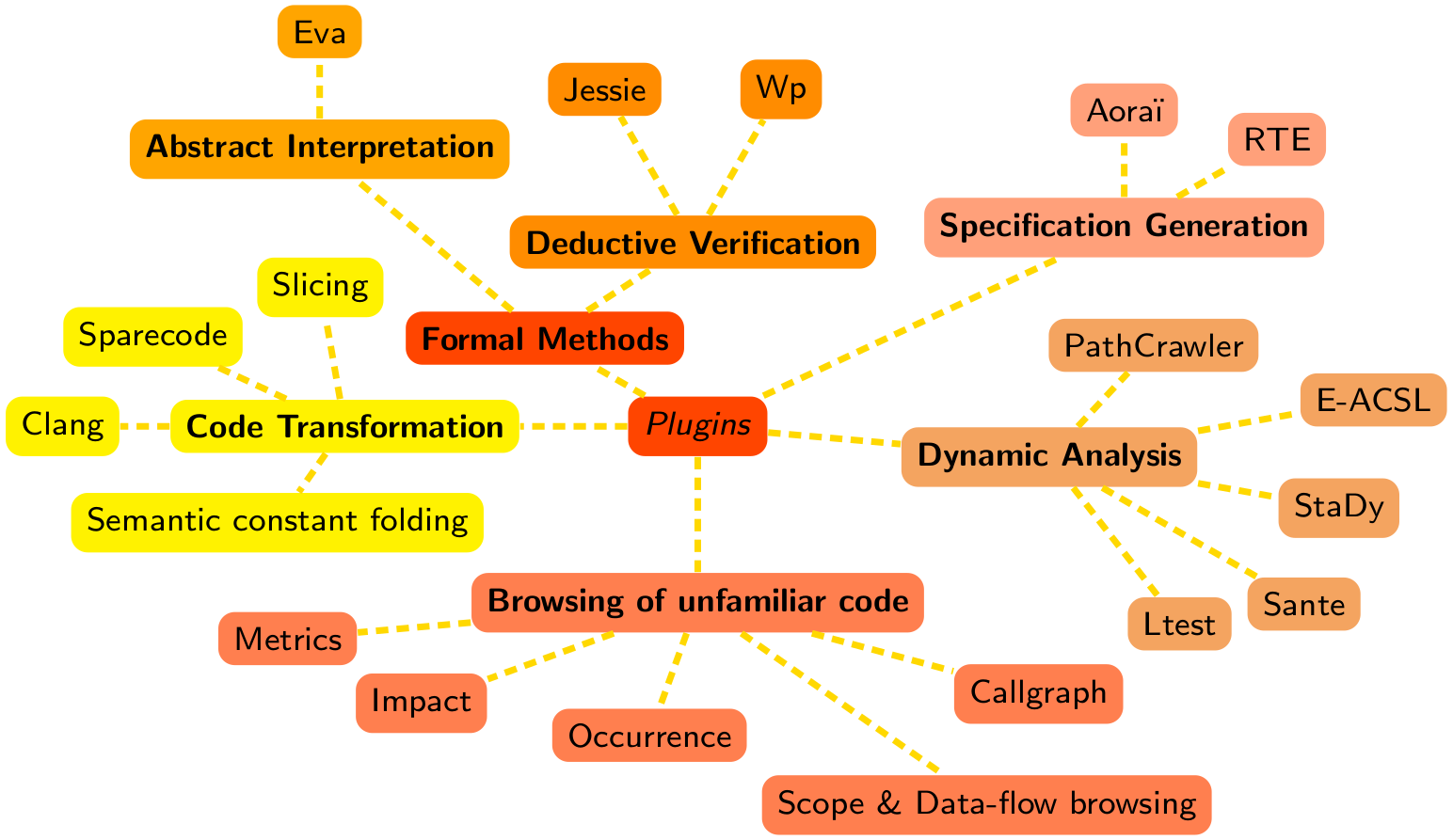
Ce langage de spécification s’appelle ACSL (« Axel ») pour ANSI C Specification Language et permet d’exprimer les propriétés que nous souhaitons vérifier sur nos programmes. Ces propriétés seront écrites sous forme d’annotations dans les commentaires. Pour les personnes qui auraient déjà utilisé Doxygen, ça y ressemble beaucoup, sauf que tout sera écrit sous forme de formules logiques. Tout au long de ce tutoriel, nous parlerons beaucoup d’ACSL donc nous ne nous étendrons pas plus à son sujet ici.
L’analyse que nous utiliserons ici est fournie par un plugin appelé WP pour Weakest Precondition, un plugin de vérification déductive. Il implémente la technique dont nous avons parlé plus tôt : à partir des annotations ACSL et du code source, le plugin génère ce que nous appelons des obligations de preuves, qui sont des formules logiques dont nous devons vérifier si elles sont vraies ou fausses (on parle de « satisfiabilité »). Cette vérification peut être faite de manière manuelle ou automatique, ici nous n’utiliserons que des outils automatiques.
Nous utiliserons en l’occurrence un solveur de formules SMT (satisfiabilité modulo théorie, et nous n’entrerons pas dans les détails). Ce solveur se nomme Alt-Ergo, initialement développé par le Laboratoire de Recherche en Informatique d’Orsay, aujourd’hui maintenu par OCamlPro.
Installation
Frama-C est un logiciel développé sous Linux et OSX. Son support est donc bien meilleur sous ces derniers. Il existe quand même de quoi faire une installation sous Windows et en théorie l’utilisation sera sensiblement la même que sous Linux, mais :
- le tutoriel présentera le fonctionnement sous Linux et l’auteur n’a pas expérimenté les différences d’utilisation qui pourraient exister avec Windows ;
- les versions récentes de Windows 10 permettent d’utiliser Windows Subsystem for Linux, en combinaison avec un Xserver installé sous Windows pour avoir la GUI ;
- La section « Bonus » un peu plus loin dans cette partie pourrait ne pas être accessible.
Linux
Via les gestionnaires de paquets
Sous Debian, Ubuntu et Fedora, il existe des paquets pour Frama-C. Dans ce cas, il suffit de taper cette ligne de commande :
apt-get/yum install frama-c
Par contre, ces dépôts ne sont pas systématiquement à jour. En soi, ce n’est pas très gênant car il n’y a pas de nouvelle version de Frama-C tous les deux mois, mais il est tout de même bon de le savoir.
Les informations pour vérifier l’installation sont données dans la sous-section « Vérifier l’installation ».
Via opam
La deuxième solution consiste à passer par Opam, un gestionnaire de paquets pour les bibliothèques et applications OCaml.
D’abord, Opam doit être installé et configuré sur votre distribution (voir leur documentation). Ensuite, il faut également que quelques paquets de votre distribution soient présents préalablement à l’installation de Frama-C. Sur la plupart des distributions nous pouvons demander à Opam d’aller chercher les bonnes dépendances pour le paquet que nous voulons installer. Pour cela, nous utilisons l’outil depext d’Opam, qu’il faut d’abord installer :
opam install depext
Puis nous lui demandons de prendre les dépendances de Frama-C :
opam depext frama-c
Si depext ne trouve pas les dépendances pour votre distribution, les paquets suivant doivent être présents sur votre système :
- GTK2 (development library)
- GTKSourceview 2 (development library)
- GnomeCanvas 2 (development library)
- autoconf
Sur les versions récentes de certaines distributions, GTK2 peut ne pas être disponible. Dans ce cas, ou si vous voulez avoir GTK3 et pas GTK2, les paquets GTK2, GTKSourceview2 et GnomeCanvas2 doivent être remplacés par GTK3 et GTKSourceview3.
Enfin, du côté d’Opam, il reste à installer Frama-C et Alt-Ergo.
opam install frama-c
opam install alt-ergo
Les informations pour vérifier l’installation sont données dans la sous-section « Vérifier l’installation ».
Via une compilation « manuelle »
Pour installer Frama-C via une compilation manuelle, les paquets indiqués dans la section Opam sont nécessaires (mis à part Opam lui-même bien sûr). Il faut également une version récente d’Ocaml et de son compilateur (y compris vers code natif). Il est aussi nécessaire d’installer Why3, en version 1.2.0, qui est disponible sur Opam ou sur leur site web (Why3).
Après décompression de l’archive disponible ici : http://frama-c.com/download.html (Source distribution). Il faut se rendre dans le dossier et exécuter la commande :
autoconf && ./configure && make && sudo make install
Les informations pour vérifier l’installation sont données dans la sous-section « Vérifier l’installation ».
OSX
L’installation sur OSX passe par Homebrew et Opam. L’auteur n’ayant personnellement pas d’OSX, voici une honteuse paraphrase du guide d’installation de Frama-C pour OSX.
Pour les utilitaires d’installation et de configuration :
> xcode-select --install
> open http://brew.sh
> brew install autoconf opam
Pour l’interface graphique :
> brew install gtk+ --with-jasper
> brew install gtksourceview libgnomecanvas graphviz
> opam install lablgtk ocamlgraph
Dépendances pour alt-ergo :
> brew install gmp
> opam install zarith
Frama-C et prouveur Alt-Ergo :
> opam install alt-ergo
> opam install frama-c
Les informations pour vérifier l’installation sont données dans la sous-section « Vérifier l’installation ».
Windows
Actuellement, la meilleure manière d’utiliser Frama-C sous Windows est de passer par Windows Subsystem for Linux. Une fois que le sous-système Linux est installé dans Windows, il suffit d’installer Opam et de suivre les instructions d’installation fournies dans la section Linux. Notons que pour profiter de l’interface graphique, il faudra installer un serveur X sous Windows.
Les informations pour vérifier l’installation sont données dans la sous-section « Vérifier l’installation ».
Vérifier l’installation
Pour vérifier votre installation, commencez par mettre ce code très simple dans un fichier « main.c » :
/*@
requires \valid(a) && \valid(b);
assigns *a, *b;
ensures *a == \old(*b);
ensures *b == \old(*a);
*/
void swap(int* a, int* b){
int tmp = *a;
*a = *b;
*b = tmp;
}
int main(){
int a = 42;
int b = 37;
swap(&a, &b);
//@ assert a == 37 && b == 42;
return 0;
}
Ensuite, depuis un terminal, dans le dossier où ce fichier a été créé, lancez Frama-C avec la commande suivante :
frama-c-gui -wp -rte main.c
Cette fenêtre devrait s’ouvrir.
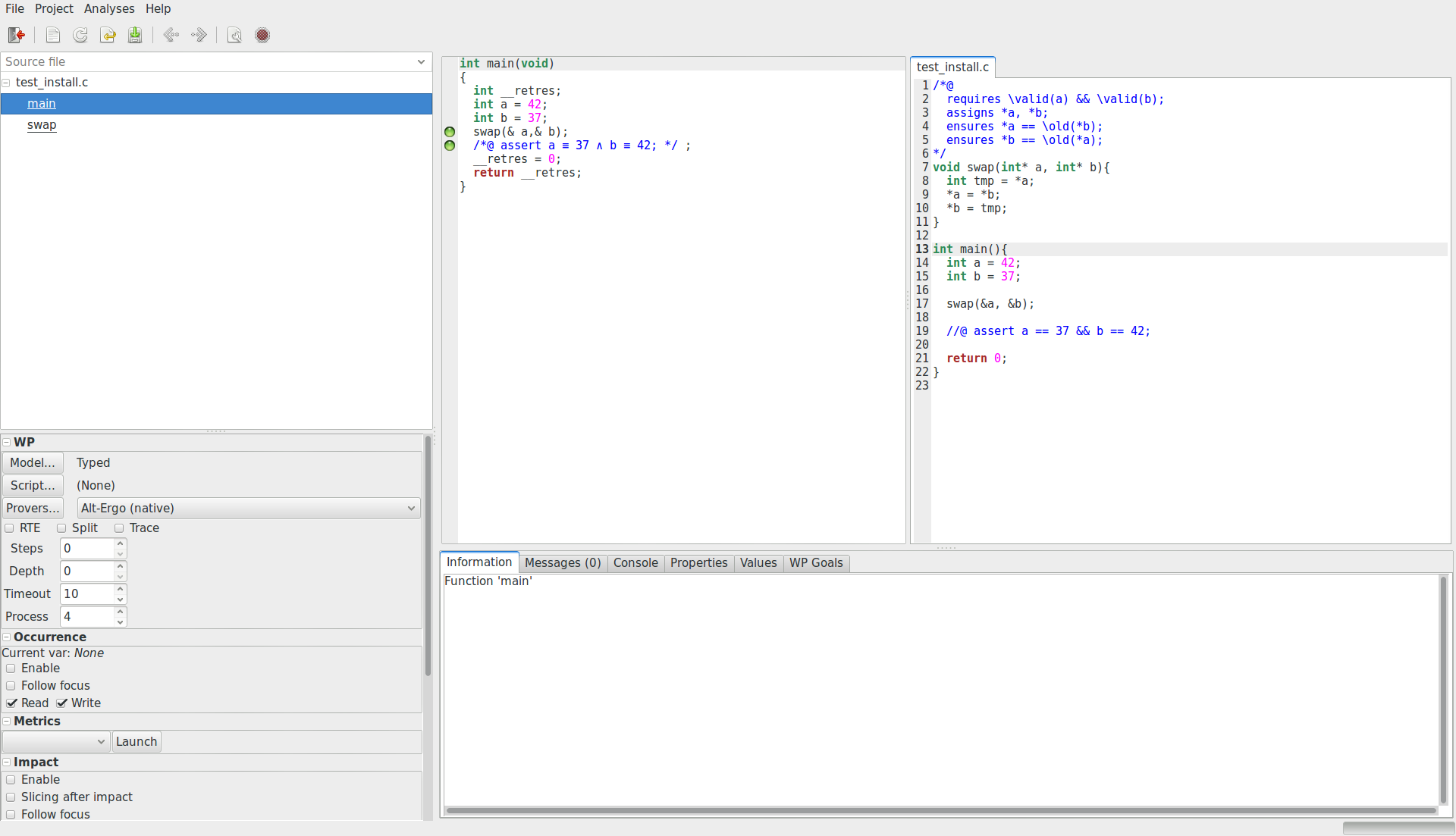
En cliquant sur main.c dans le volet latéral gauche pour le sélectionner,
nous pouvons voir le contenu du fichier main.c modifié et des pastilles
vertes sur différentes lignes comme ceci :
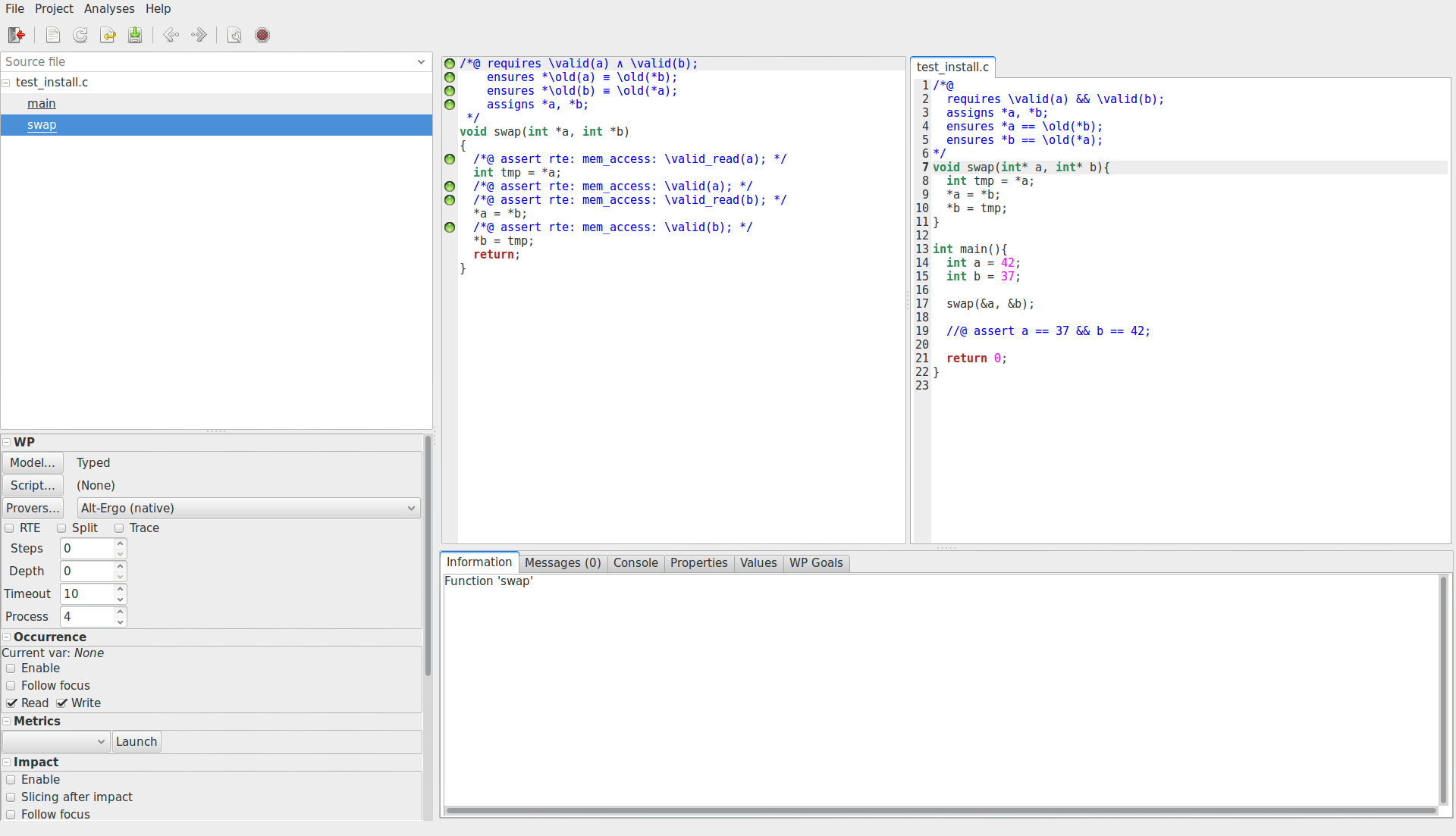
Si c’est le cas, tant mieux, sinon il faudra d’abord vérifier que rien n’a été oublié au cours de l’installation (par exemple : l’oubli de bibliothèques graphiques ou encore l’oubli de l’installation d’Alt-Ergo). Si tout semble correct, divers forums pourront vous fournir de l’aide (Forum de Zeste de Savoir, StackOverflow - Frama-C).
L’interface graphique de Frama-C ne permet pas l’édition du code source.
Pour les daltoniens, il est possible de lancer Frama-C avec un mode où les pastilles de couleurs sont remplacées par des idéogrammes noirs et blancs :
frama-c-gui -gui-theme colorblind
(Bonus) Installation de prouveurs supplémentaires
Cette partie est purement optionnelle, rien de ce qui est ici ne sera indispensable pendant le tutoriel. Cependant, lorsque l’on commence à s’intéresser vraiment à la preuve, il est possible de toucher assez rapidement aux limites du prouveur pré-intégré Alt-Ergo et d’avoir besoin d’autres prouveurs. Pour des propriétés simples, tous les prouveurs jouent à armes égales, pour des propriétés complexes, chaque prouveur à ses domaines de prédilection.
Why3
Why3 est une plateforme pour la preuve déductive développée par le LRI à Orsay. Elle embarque en outre un langage de programmation et de spécification ainsi qu’un module permettant le dialogue avec une large variété de prouveurs automatiques et interactifs. C’est en cela qu’il est utile dans le cas de Frama-C et WP. WP utilise Why3 comme backend pour dialoguer avec les prouveurs externes.
Nous pouvons retrouver sur leur site la liste des prouveurs qu’il supporte. Il est vivement conseillé d’avoir Z3, développé par Microsoft Research, et CVC4, développé par des personnes de divers organismes de recherche (New York University, University of Iowa, Google, CEA List). Ces deux prouveurs sont très efficaces et relativement complémentaires.
De nouveaux prouveurs peuvent être installés n’importe quand après l’installation de Frama-C. Cependant la liste des prouveurs vus par Why3 doit être mise à jour :
why3 config --full-config
puis activée dan Frama-C. Dans le panneau latéral, dans la partie WP, cliquons sur « Provers… » :
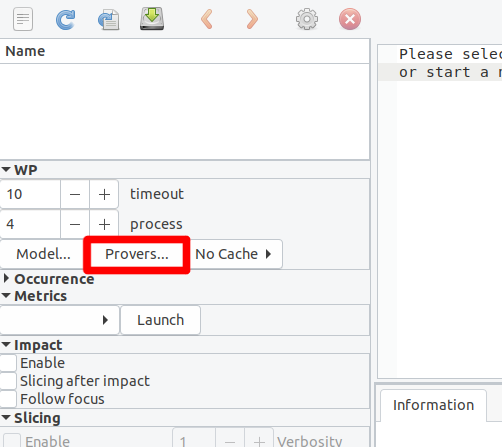
Puis « Detect » dans la fenêtre qui apparaît. Une fois que c’est fait, les prouveurs peuvent être activés grâce au bouton qui se trouve à côté de leur nom.
Coq
Coq, développé par l’organisme de recherche Inria, est un assistant de preuve. C’est-à-dire que nous écrivons nous-même les preuves dans un langage dédié, et la plateforme se charge de vérifier (par typage) que cette preuve est valide.
Pourquoi aurait-on besoin d’un tel outil ? Il se peut parfois que les propriétés que nous voulons prouver soient trop complexes pour un prouveur automatique, typiquement lorsqu’elles nécessitent des raisonnements par induction avec des choix minutieux à chaque étape. Auquel cas, WP pourra générer des obligations de preuve traduites en Coq et nous laisser écrire la preuve en question.
Pour apprendre à utiliser Coq, ce tutoriel est très bon.
Si Frama-C est installé par l’intermédiaire du gestionnaire de paquets, il peut arriver que celui-ci ait directement intégré Coq.
Pour plus d’informations à propos de Coq et de son installation, voir The Coq Proof Assistant.
Le support actuel de Coq dans Frama-C est déprécié mais toujours accessible. Comme nous fournissons dans ce tutoriel quelques scripts de preuve Coq qui peuvent être utilisés, nous fournissons ces instructions afin que ces scripts puissent être visionnés et testés par les utilisateurs. Pour lancer Frama-C avec le support de Coq, nous utilisons la commande :
frama-c -wp-provers=native:coq
Voilà. Nos outils sont installés et prêts à fonctionner.
Le but de cette partie, en plus de l’installation de nos outils de travail pour la suite, est de faire ressortir deux informations claires :
- la preuve est un moyen d’assurer que nos programmes n’ont que des comportements conformes à notre spécification sans les exécuter ;
- il est toujours de notre devoir d’assurer que cette spécification est correcte.