Bon, maintenant que vous avez dans votre boîte à outil quelques algorithmes, il est temps d'éprouver leur efficacité et leur polyvalence.
Vous allez voir ici les problèmes de graphe les plus classiques : nous allons les résoudre de façon élégante en adaptant ce que nous avons vu précédemment.
Et puis, comme d'habitude, je ne saurais que trop vous conseiller de chercher la solution avant d'aller regarder la correction ! C'est ainsi que vous développerez une plus grande autonomie face à ce type de problèmes.
Le tri topologique et make
make est un utilitaire mis au point en 1977 par Stuart Feldman permettant d'automatiser la génération de fichiers à partir de règles simples (et éventuellement en faisant appel à d'autres programmes ou à la ligne de commande). Il est souvent utilisé pour fabriquer des fichiers exécutables ou des bibliothèques à partir des fichiers sources et d'un compilateur.
Les projets de grande envergure qui contiennent un nombre important de fichiers ont rendu indispensable l'utilisation de ce type d'outils.
Le (ou les) fichiers que l'on cherche à produire (appelés fichiers cibles) dépendent de la fabrication de plusieurs autres fichiers "intermédiaires", qui eux même peuvent dépendre de la création de plusieurs autres fichiers, et ainsi de suite jusqu'aux fichiers qui étaient déjà présents au début du processus (les fichiers source).
Les dépendances entre les différents fichiers, et la liste de commande permettant de créer chacun d'eux, sont spécifiées par le programmeur dans un fichier appelé Makefile que le programme make va lire.
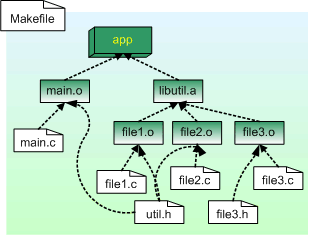
Vous avez pour mission de programmer l'un des composants du logiciel présenté ci-dessus. Vous devez créer un algorithme qui prend en entrée une liste de dépendances entre différents fichiers, et retourne un ordre de construction valide des fichiers.
Commencez par formaliser les caractéristiques du graphe.
- Ce graphe peut être cyclique ! Nous ne sommes pas à l'abri d'un programmeur négligeant qui aurait rendu certains fichiers mutuellement dépendants. Nous devons donc détecter ces cas particuliers et afficher une erreur le cas échéant.
- Ce graphe est clairement orienté. Une dépendance est (normalement) à sens unique.
- Ce graphe n'est pas pondéré.
- Le graphe peut ne pas être connexe si le programmeur spécifie plusieurs cibles totalement indépendantes dans son makefile. Toutefois, on peut se ramener à un graphe connexe grâce à une petite astuce ! On peut créer une cible "globale" abstraite (liée à aucun fichier physique) qui aurait pour dépendance toutes les autres cibles concrètes. C'est d'ailleurs ainsi que procède make.
Ne lisez pas tout de suite la correction !
A présent, vous disposez normalement d'un bagage suffisant pour trouver l'algorithme approprié en vous appuyant sur ceux que nous avons vu précédemment.
Forcez-vous à chercher, c'est ainsi que vous progresserez.
Solution
Ici, comme souvent, formaliser ce qu'on fait naturellement à la main suffit à obtenir l'algorithme.
Une méthode naturelle consiste à prendre un fichier qui ne dépend d'aucun d'autre, et l'ajouter à la liste des fichiers à traiter. Par la suite, les fichiers qui en dépendaient n'auront plus cette contrainte pour exister, puisque le fichier requis aura été considéré comme traité.
Puis prendre un nouveau fichier, qui ne dépend d'aucun autre, ou qui ne dépend que de celui que l'on vient de traiter, et l'ajouter (en respectant les ordres d'ajout successifs) à la liste des fichiers à traiter.
Et répéter ainsi l'opération qui consiste à ne traiter que les nœuds pour lesquels on a résolu toutes les dépendances. Cet algorithme est nommé Tri Topologique.
Si à la fin il reste encore des nœuds non traités mais qu'ils sont tous dépendants, alors cela signifie qu'il y a un cycle. Autrement dit, le problème n'est pas soluble.
Et comment déterminer efficacement si un nœud dépend d'un autre ?
Eh bien en regardant son degré entrant pardi !
On peut ainsi modifier dynamiquement le graphe de façon très simple : pour supprimer un nœud on supprime toutes ses arêtes sortantes, et par conséquent on réduit donc de 1 le degré entrant des nœuds de destination.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | explorer(Graphe G, Noeud N)
{
Liste ordreTotal = {N}
Pour chaque voisin V de N
V.degreEntrant -= 1
Si V.degreEntrant == 0
noeudsTries = explorer(G, V)
ordreTotal.concatener(noeudsTries)
Renvoyer ordreTotal
}
TriTopologique(Graphe G)
{
Liste ordreTotal
Pour chaque noeud N dans G
Si N.degreEntrant == 0
noeudsTries = explorer(N)
ordreTotal.concatener(noeudsTries)
Si ordreTotal.taille < G.nbNoeuds
Afficher "Cycle detecte, resolution des dependances impossible"
Sinon
Afficher ordreTotal
}
|
Remarquez la fonction explorer : elle est construite sous la forme d'une fonction exploration récursive fortement semblable à celle du DFS.
Ainsi, comme je vous l'avais précédemment dit, les algorithmes classiques (moyennant quelques modifications mineures) permettent de résoudre un nombre très varié de problèmes. Gardez cela en tête !