Nous voici à la fin de cette première partie du tutoriel.
Je suis vraiment heureux que vous en soyez arrivés là : cela prouve que vous êtes motivés et déterminés, ça fait plaisir à voir  .
.
Le titre de ces deux chapitres de conclusion est assez évocateur et j'espère que vous vous plairez à les lire. Nous allons apprendre ensemble à transformer un calque et à le déformer à notre guise. Autant de techniques de travail qu'il est impératif de maitriser si vous voulez donner un sens à vos futures créations.
Cette première sous-partie fera l'objet d'une « minute théorique » sur le thème de la symétrie. Un bref récapitulatif pour ceux à qui le collège remonte loin, et la possibilité de découvrir de quoi il s'agit pour les plus jeunes d'entre nous.
C'est le moment pour vous de vous reposer un peu en attendant le reste du chapitre.
- La minute théorique : transformer à l'aide de la symétrie
- Symétrie des axes
- Rotation
- Transformation en homothétie
- Inclinaison
La minute théorique : transformer à l'aide de la symétrie
Le terme de "transformation" est employé pour diverses raisons, en fonction des domaines pratiqués. Transformer un calque sur Photoshop, c'est le transformer géométriquement.
On a tous suivi des cours de géométrie au moins une fois dans sa vie à l'école ? Et bien le principe est le même. Pour tracer un rond au compas ou bien un carré à la règle, on utilise les axes X et Y, respectivement appelés abscisse et ordonnée. Plus exactement, on détermine une position géométrique sur ces deux axes, qui sont perpendiculaires entre-eux, puis on trace une figure géométrique en les utilisant comme base.
Sur Photoshop, on retrouve les axes X et Y dans la zone de travail :
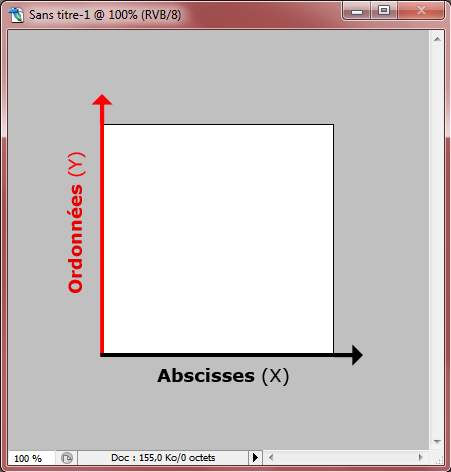
Ainsi, on effectue des modifications sur ces deux axes : de haut en bas (on ne travaillerait alors que sur l'axe Y), de bas en haut (idem, on transforme le calque sur l'axe Y), de gauche à droite (ici, on modifie le calque sur l'axe X), de droite à gauche (idem, axe X), mais aussi pourquoi pas du bas droit vers le haut gauche (on transformerait alors le calque sur la diagonale, à savoir sur les deux axes : X et Y), ou du haut droit vers le bas gauche (X et Y aussi).
La symétrie, c'est quoi ?
Nous allons nous intéresser à plusieurs types de symétrie. Il m'a semblé plus prudent de passer par là avant d'étudier les fonctionnalités faisant l'objet de ce chapitre et du suivant.
Symétrie axiale
Le premier type de symétrie dont je souhaite vous parler se nomme symétrie axiale. Pour la comprendre, il suffit de prendre une feuille sur laquelle sont dessinées deux figures. Si on plie correctement la feuille en deux et que ces deux figures se superposent, alors on dit qu'elles sont symétriques par rapport à la pliure.
On arrive plus facilement à s'imaginer ce qu'est un centre de symétrie avec l'exemple du terrain de football que voici.
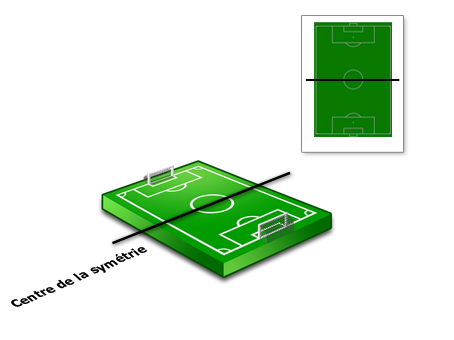
La première moitié d'un terrain de football est parfaitement symétrique par rapport à l'autre, la ligne blanche du milieu étant l'axe à partir duquel la symétrie est formée, vous saisissez l'idée ?  Si l'on décale légèrement chaque moitié du terrain par rapport à leur ligne du milieu…
Si l'on décale légèrement chaque moitié du terrain par rapport à leur ligne du milieu…
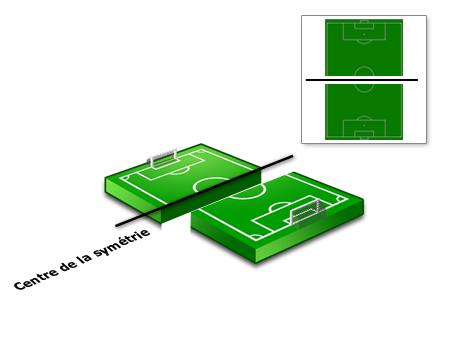
Symétrie centrale
Si nous avions besoin d'un axe de symétrie pour la symétrie axiale, nous aurons cette fois besoin d'un point de symétrie. De ce fait, on dira de deux objets qu'ils sont "symétriques" par rapport à un point. Petite piqûre de rappel sur la construction d'une symétrie centrale :
- On dessine un point, qui est notre point de symétrie
- On trace notre figure géométrique (en prenant l'exemple d'un losange)
 - On trace un trait partant de chaque sommet du losange vers le point de symétrie.
- On trace un trait partant de chaque sommet du losange vers le point de symétrie.
 - Avec le compas, on place la pointe sur le centre de symétrie et la mine sur le sommet du triangle. On fait pivoter le compas puis on trace un arc de cercle qui vient couper la droite tracée et passant par ce même sommet et le point de symétrie.
- Avec le compas, on place la pointe sur le centre de symétrie et la mine sur le sommet du triangle. On fait pivoter le compas puis on trace un arc de cercle qui vient couper la droite tracée et passant par ce même sommet et le point de symétrie.
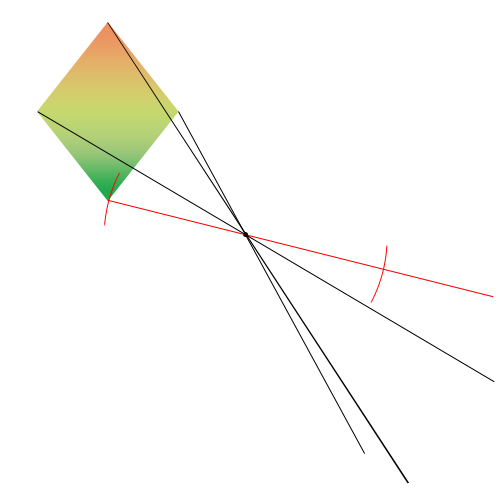 - On réitère l'opération avec tous les autres sommets.
- On réitère l'opération avec tous les autres sommets.
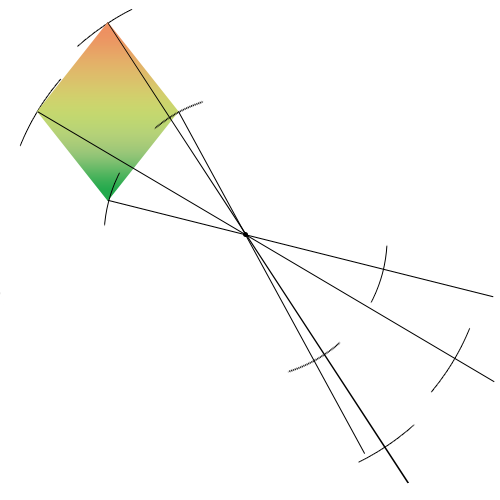 - Pour finir, on efface tous les traits en ne conservant que l'intersection entre les arcs-de-cercle et les traits.
- Pour finir, on efface tous les traits en ne conservant que l'intersection entre les arcs-de-cercle et les traits.
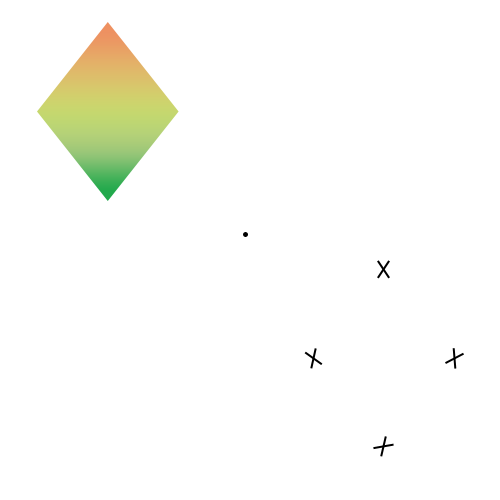
Et qu'est-ce qu'on fait avec ça ?
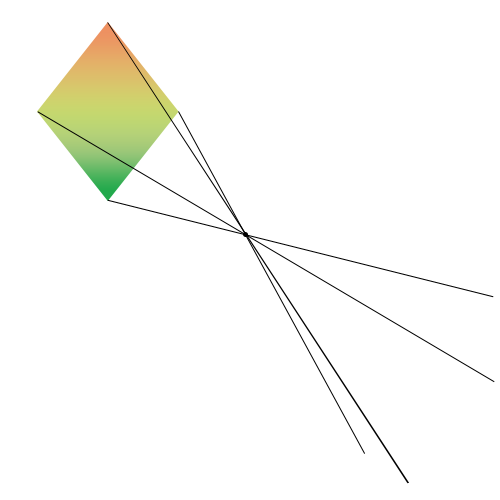
Cela m'a permis de vous expliquer le principe de la symétrie centrale. Théoriquement, si l'on devait voir le résultat de notre cheminement, on obtiendrait :
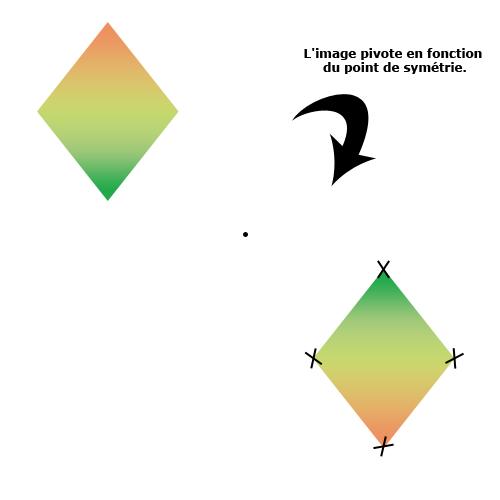
Le losange en haut à gauche est notre losange originel. Son symétrique est le losange en bas à droite (forcément). On en déduit facilement (et plus qu'une déduction, il s'agit d'une explication avérée) que le losange a pivoté autour du point de symétrie. C'est d'ailleurs la raison pour laquelle les couleurs se sont inversées (vérifiez bien)  .
.

Maintenant que ces deux notions de symétrie sont acquises, vous aurez clairement plus de facilité à saisir le fonctionnement des transformations sur Photoshop.
Symétrie des axes
Symétrie des axes
Et on commence fort puisque l'on va directement avoir affaire à la symétrie axiale. Tous les paramètres que nous nous apprêtons à étudier ne sont pas des outils à proprement dire. En tout cas, vous ne les retrouverez pas dans la boite à outils. Je dirais plutôt que ce sont des fonctionnalités de Photoshop, fonctionnalités que vous retrouverez en totalité en déroulant le menu Édition puis dans Transformation.

Les premières transformations que nous allons produire sont les deux dernières de la liste, à savoir "Symétrie axe horizontal" et "Symétrie axe vertical".
Et bien devinez quoi ? Ces deux types de transformation consistent à transformer un élément de la zone de travail… en son symétrique grâce à la symétrie axiale !
C'est parti pour un exemple illustré  .
.
N'hésitez pas à travailler avec moi ! Télécharger l'image Main_gauche.png Pour télécharger l'image, faites un clic droit sur le lien puis "Enregistrer sous…"
Voici l'image que nous allons transformer. Franchement, ce n'est vraiment pas compliqué maintenant que vous avez acquis la notion de symétrie axiale. En reprenant l'exemple de la pomme, on sait que l'on détermine le symétrique d'une image en fonction de son axe de symétrie et à partir du moment où, si l'on plie la feuille en deux à partir de cet axe, les deux images se superposent.

Ce cas est avéré sur cet exemple. Nous avons d'un côté l'image originelle et à gauche son symétrique que j'ai nommé "transformation".
Vous l'aurez donc compris, avec les transformations "Symétrie axe", on est en mesure de transformer le calque en son symétrique.
Attention, il n'est pas question de créer un nouveau calque contenant le symétrique du calque originel car en transformant le calque, vous le remplacez par son symétrique.
En d'autres termes, si l'image originelle est la suivante :

En cliquant sur "Symétrie axe horizontal", vous la transformerez sur l'axe des abscisses et c'est son symétrique qui la remplacera.

De la même manière, en transformant l'image originelle sur l'axe des ordonnées (ce qui signifie à la verticale), on la remplace par son symétrique :

D'accord, mais, va savoir pourquoi, j'ai l'impression que cette transformation n'est pas très utile, je me trompe ?
Carrément que vous vous trompez  ! Bon, après, on peut trouver nécessité à cette transformation pour différents besoins, je ne saurais dire lesquels exactement. Je peux toutefois vous donner un ou deux exemples, le premier qui me vient étant lié au domaine de la photographie. Les explications suivantes, généreusement fournies par victor, fidèle membre du Site du Zéro reconnu pour
! Bon, après, on peut trouver nécessité à cette transformation pour différents besoins, je ne saurais dire lesquels exactement. Je peux toutefois vous donner un ou deux exemples, le premier qui me vient étant lié au domaine de la photographie. Les explications suivantes, généreusement fournies par victor, fidèle membre du Site du Zéro reconnu pour son mauvais caractère ses talents de photographe, vous permettront d'en apprendre davantage sur le sens directionnel d'une photo,
Quand on prend une photo, il faut prendre en considération le sens de la lecture. En Europe et en Occident de manière générale, on lit de gauche à droite. Ainsi, dans les régions où on lit de gauche à droite, faire "regarder" le sujet d'une photo vers la droite donne une illusion d'ouverture.
Faire regarder le sujet vers la gauche produit l'effet inverse : fermeture.
C'est très présent dans la façon d'appréhender et de comprendre une image chez les photographes, et même si c'est totalement inconscient chez la majorité des gens qui ne sont pas forcément renseignés, cela influence énormément votre lecture (on parle de lecture d'image pour dire appréhension, compréhension) d'une image (à votre insu).
Exemple
Une voiture qui se dirige vers la droite donne l'impression de partir. Si elle va vers la gauche de l'image, on pensera alors qu'elle arrive.
Idem pour un objet volant. Par exemple l'avion ou l'oiseau, pour faire croire qui s'élève dans le ciel, devra le faire d'en bas à gauche à en haut à droite. L'inverse, d'en bas à droite à en haut à gauche, serait en quelque sorte inesthétique pour des raisons purement liées à la photographie. Je peux te parler par exemple de la lecture en Z, mais ça, c'est une autre histoire (qui aurait beaucoup plus sa place dans un article de photographie que dans un cours dédié à Photoshop)
…
Du coup, on peut avoir recours à cette transformation quand on a besoin de modifier la direction de notre sujet :
Ici, on peut se poser une question : lequel de ces couloirs est celui d'où on est venu et lequel celui où nous allons ?
victor
Une notion importante est à signaler au sujet de la transformation de type "miroir" (comme on vient de le faire avec la main). En effet, celle-ci est à proscrire sur du texte ou un objet, une personne ou un paysage reconnaissable. Une fois transformée sur l'axe des X ou des Y, le sujet de l'image peut ne plus être reconnaissable et votre transformation perdrait alors toute sa crédibilité. Par exemple, l'image suivante présente un appareil photo des plus traditionnels.
Pourquoi n'est-il pas permis de transformer cette photo sur l'axe des abscisses de sorte à créer un effet "miroir" à l'exemple de l'image ci-dessous à votre avis ?

Outre le problème posé par l'inversion du texte, la transformation symétrique de cette image montre un appareil photo qui n'existe pas dans la réalité. Ou alors… ce serait un appareil "pour gaucher", vu qu'il forcerait son utilisateur à faire tout à l'inverse des appareils habituels : mise au point de la main droite, déclenchement et recharge de la main gauche … Vous saisissez ? 
L'utilisation de cette transformation du texte n'est toutefois pas impossible ! On peut par exemple sans problème profiter de la symétrie verticale pour créer un effet assez sympa, j'ai justement prévu un exemple pour vous. Ainsi, on partirait de ce texte :

Admettons que l'on veuille créer une sorte de reflet à partir de ces textes. On va alors devoir dupliquer le calque du texte (on verra plus tard comment créer un calque de texte) et lui diminuer le pourcentage d'opacité de ce nouveau calque.

Enfin, on transforme ce nouveau calque verticalement et on le colle comme ceci au calque d'origine.

Comme quoi, on peut en faire des choses, avec ces deux transformations mine de rien  .
.
Rotation
Je vous rappelle que toutes les transformations se trouvent dans le même menu (Édition > Transformation).
Nous allons à présent utiliser la transformation nommée "Rotation". Sur Photoshop, la rotation désigne le fait d'effectuer un mouvement autour d'un seul et même point. Si vous avez bien suivi le chapitre, ce que je viens de dire devrait faire "tilt"… Vous voyez où je veux en venir ? Je veux faire référence au fameux point de symétrie que nous avons rencontré lors de mon explication sur la symétrie centrale. On va donc avoir affaire à elle (comme par haaaasard !  ) !
) !
Un exemple arrive, n'hésitez pas à travailler avec moi ! Télécharger les deux fichiers sources : : fichier 1 - fichier 2 Rotation.psd - Horloge.png (Faites un clic droit puis 'Enregistrer sous…' pour télécharger cette dernière)
Voici les images sur lesquelles je vais vous expliquer comment cela fonctionne.
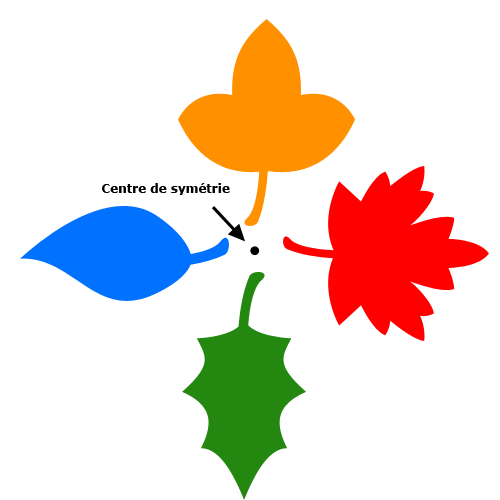
Souvenez-vous, la symétrie centrale se construit à l'aide d'un élément essentiel : le point de symétrie (déjà répété maintes et maintes fois). On se souvient alors que l'on avait tracé des droites puis des arcs de cercle permettant de créer le squelette du symétrique. Je vous rassure, nous n'aurons pas besoin de faire tout cela : tout est automatisé, nous n'aurons qu'à cliquer sur des boutons figurant dans le menu Transformation. D'ailleurs, en déroulant ce menu (Édition > Transformation), on a droit à trois fonctionnalités :
- Rotation 180°
- Rotation 90° horaire
- Rotation 90° antihoraire
Ces trois boutons vont nous permettre de définir un angle de rotation.
- Rotation 180° : on fait pivoter) la figure en fonction du point de symétrie sur 180°
- Rotation 90° horaire : on fait pivoter la figure autour du point de symétrie dans le sens des aiguilles d'une montre sur 90°
- Rotation 90° antihoraire : même fonctionnement, sauf que la rotation se fait dans le sens contraire des aiguilles d'une montre sur 90°
On donne alors trois angles à partir desquels l'élément sélectionné va effectuer une rotation, vous saisissez ?
Je vous présente le résultat de la transformation lorsque l'on demande à l'image d'effectuer une rotation à 90° horaire.
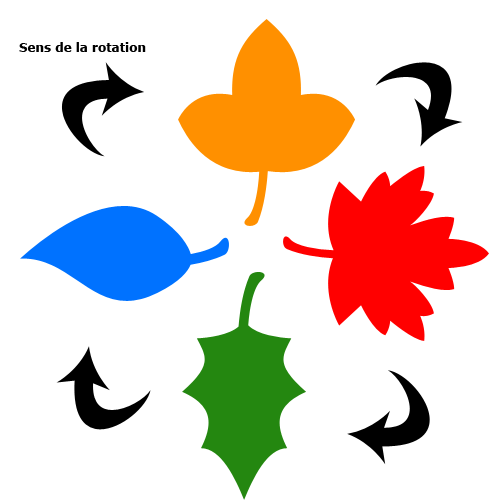

Sur notre horloge sans chiffre, le sens a changé. On peut notamment s'en rendre compte à l'aide du reflet visible sur le fond noir de l'horloge :
Et maintenant, le résultat une fois une rotation à 90° de type antihoraire effectuée.
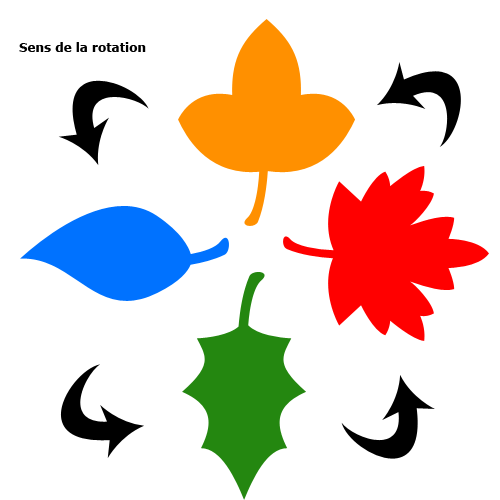
De la même manière, toutes les feuilles ont été déplacée de 90° mais dans le sens contraire d'une aiguille d'une montre.

Quand on fait pivoter un élément à 90°, il faut juste "imaginer" que l'image de base est à l'origine présentée à l'horizontale pour se rendre compte qu'il s'agit bel et bien d'une symétrie centrale  .
.
A l'image des transformations "Symétrie axe", une fois l'élément transformé, il est remplacé par son symétrique.
Transformation en homothétie
L'homothétie est une transformation géométrique. Les définitions que l'on peut trouver sur la toile sont assez compliquées, on va se contenter d'utiliser la transformation pour comprendre son fonctionnement, ce sera plus explicite pour vous.
Jusqu'ici, nous n'avons pas eu besoin de manipuler quoi que ce soit. Tout ce que l'on a fait, c'est cliquer sur des boutons du menu à partir desquels une transformation s'effectuait automatiquement. Cette fois-ci, si nous cliquons sur le bouton Homothétie dans le menu Transformation, nous ne faisons qu'activer la fonctionnalité. Cela signifie qu'il faut l'utiliser manuellement avec la souris de son ordinateur.
Un exemple arrive, n'hésitez pas à travailler avec moi ! Télécharger l'image SdZ.png
Pour cet exemple, je travaillerai sur ce document :

On aura tous reconnu le devenu-célébrissime logo du Site du Zéro. En allant chercher la transformation dans Édition > Transformation > Homothétie et en cliquant dessus, je m'aperçois d'un changement au sein de ma zone de travail : une sorte de cadre apparait.

Ce cadre signifie que la transformation est activée : nous allons pouvoir effectuer la transformation. Notre travail, à nous, consistera à déplacer les petits carrés transparents que l'on peut apercevoir aux bords et aux coins de l'image.
Pour cela, il suffit simplement de maintenir le clic sur l'un des carrés et de déplacer le curseur de sa souris. En le déplaçant, on va entrainer avec nous le carré transparent, qui lui va entrainer avec lui et étirer le logo.
D'accord, mais en quoi l'homomachin est-elle une symétrie ?
La définition proposée par Wikipédia est particulièrement difficile à comprendre. Pour faire simple, je peux vous dire que cette transformation telle qu'on l'utilise en infographie va nous permettre de réduire ou agrandir une image sur la largeur ou la hauteur. Techniquement, c'est un peu plus complexe, mais on s'en tiendra à cette définition si vous le voulez bien.
Nous avons la possibilité de modifier la position de 8 carrés transparents : 4 aux coins et 4 sur les arêtes (c'est-à-dire les bords de l'image, pas besoin de vous faire un dessin non plus). Chaque carré permet de transformer l'élément encadré (ici, le logo du Site du Zéro). Par exemple, en travaillant sur le carré suivant, on va être en mesure de modifier la hauteur du cadre (et donc de l'image, puisque qu'il va l'entrainer avec lui).
De même, en travaillant sur le carré gauche situé au bord de l'image, on peut modifier la largeur de cette dernière :

Enfin, en modifiant la position de l'un des carrés transparents situés aux coins de l'image, on peut modifier la taille générale de l'image, c'est-à-dire la rétrécir sur la largeur et/ou sur la hauteur, autrement dit sur la diagonale.

Il faut maintenir le clic sur le carré transparent pour pouvoir le déplacer avec le curseur. Pour cet exemple, j'ai commencé par déplacer le carré transparent situé en haut, sur le bord de mon image. J'ai eu deux choix : soit agrandir la hauteur du calque, soit la rétrécir. Pour le coup, je l'ai rétrécie :

Remarque : sur l'exemple ci-dessus, on peut apercevoir en fond l'image originelle, c'est-à-dire celle qui n'a pas été transformée. Ne vous laissez pas tromper, c'est pour l'exemple uniquement  .
.
Pour valider la transformation (c'est-à-dire retirer le cadre et donc laisser l'image telle qu'on l'a transformée), j'ai utilisé la touche Entrée de mon clavier. Notez que j'aurais très bien pu cliquer sur le bouton suivant dans la barre des options : 
 .
.

Qu'est-ce que cela donne si je déplace l'un des carrés transparents situés aux coins de l'image ?
Comme je vous l'ai dit, si l'on déplace l'un de ces petits carrés, nous pouvons transformer le calque sur l'axe X et Y (abscisses et ordonnées) c'est-à-dire sa largeur ET sa hauteur (on va alors effectuer un déplacement en diagonale). Faisons un essai  .
.
Pour effectuer une transformation de manière proportionnelle, il faut appuyer simultanément sur la touche Shift de votre clavier d'ordinateur.
Pour cet exemple, je travaillerai sur ce petit carré transparent.

Je vais alors cliquer dessus et appuyer simultanément sur ma touche Shift afin d'effectuer une diminution des tailles de l'image de manière proportionnelle.

On constate que l'image a globalement rétréci. Je valide ensuite la transformation, et voici le résultat obtenu !

Par comparaison, on remarque le changement de taille radical :

Transformer en homothétie, pour quoi faire ?
C'est une question qui va souvent revenir dans ce chapitre et celui qui suit. C'est la raison pour laquelle je vais, chaque fois que je juge nécessaire de le faire, vous proposer un exemple concret de ce à quoi peut servir telle ou telle transformation. Ainsi, vous pourrez vous faire une idée de l'utilité de chacune d'entre elles  .
.
L'exemple que j'ai choisi pour l'homothétie est basé sur l'incrustation d'une image dans un écran de télévision. On va donc commencer par choisir une télévision  .
.

J'ai alors cherché une image relative à la télévision à insérer dans cet écran. Allez savoir pourquoi, la première idée qui m'est venue est… le JT ! Et qui dit JT dit… PPDA  .
.

Notre objectif sera le suivant : nous allons tenter de réduire la taille de cette image de sorte à ce que ses nouvelles dimensions nous permettent de l'insérer dans l'écran d'ordinateur. On va donc activer la transformation Homothétie avant de rétrécir l'image puis de la placer au niveau de l'écran.

Un nouvel exercice amusant !
Et si nous travaillions l'homothétie d'une toute autre manière ? On pourrait par exemple utiliser deux images aux sujets communs mais aux échelles différentes…
Mais qu'est-ce qu'il est en train de me raconter, là… ? 
Pour illustrer l'homothétie, victor m'a suggéré un petit exercice de mise à l'échelle. Il m'a fourni deux photos que je vous présente ci-dessous. Chacune d'elles présente un appareil photo et une règle. Votre mission, si vous l'acceptez, consiste à "réunir" ces deux photos en une seule et même image sur laquelle les appareils photos apparaitront à la même échelle, ceci parce que l'on va faire superposer les mesures des deux règles et pour que l'on se rende bien compte de leur différence de taille.
 Konica - © vhf/victor
Konica - © vhf/victor
 Minox - © vhf/victor
Minox - © vhf/victor
N'hésitez pas à travailler avec moi ! Télécharger l'image KONICA Konica.jpg Télécharger l'image MINOX Minox.jpg Pour télécharger les images, faites un clic droit sur les liens puis "Enregistrer sous…"
Voici les consignes : on va chercher dans un premier temps à superposer les deux images. Ensuite, pour réussir l'exercice, nous allons réduire l'image de l'appareil photo Minox à l'aide de l'homothétie de sorte à ce que les mesures de la règle se superposent à celles de la règle de l'image du Konica.
Veuillez tout d'abord créer une nouvelle zone de travail aux dimensions supérieures à celles des deux images. Par exemple : 800*650px. On aura ainsi toute la place pour travailler  .
Puis, veuillez copier et coller les deux images ci-dessus ou les ouvrir dans Photoshop pour les faire ensuite glisser dans la zone de travail que vous venez de créer. Au final, la fenêtre de calques doit ressembler à celle-ci :
.
Puis, veuillez copier et coller les deux images ci-dessus ou les ouvrir dans Photoshop pour les faire ensuite glisser dans la zone de travail que vous venez de créer. Au final, la fenêtre de calques doit ressembler à celle-ci :
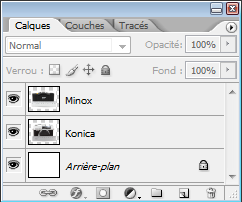
Veillez à ce que les deux calques des photos (Minox et Konica dans la fenêtre de calques ci-dessus) ne soit pas verrouillés ! Je vous signale aussi que le calque Minox doit figurer en tête de liste (pareil, comme sur la fenêtre de calques d'au-dessus) dans la fenêtre de calque. Enfin, veuillez placer l'appareil photo Minox au-dessus de l'appareil photo Konica dans votre zone de travail à l'aide de l'outil  Déplacement.
Déplacement.
Nous allons maintenant réduire le calque Minox afin que les mesures de sa règle se superposent avec celles de la règle Konica.
Petit problème : la règle Konica est totalement masquée par le calque Minox qui figure en premier plan dans la fenêtre de calques. Si vous avez bien suivi depuis le début, vous savez qu'il existe une solution très efficace qui consisterait à modifier la transparence d'un calque, en l'occurrence celui de Minox, ceci dans le but de laisser apparaitre celui de Konica  … Je vous invite alors à réduire l'opacité du calque Minox à 50% puis activer la transformation Homothétie sur ce même calque.
… Je vous invite alors à réduire l'opacité du calque Minox à 50% puis activer la transformation Homothétie sur ce même calque.

Nous allons utiliser l'homothétie afin de réduire l'image de l'appareil photo Minox pour que les mesures de sa règle se superposent à celles de la règle de l'appareil photo Konica. En d'autres termes, nous allons faire en sorte que les mesures 0 et 10 des deux règles ne fassent qu'une.

Allez-y, commencez. Utilisez l'homothétie afin de réduire proportionnellement (appuyer simultanément sur la touche Shift ou Command) l'image Minox et rassembler les deux mesures de chaque image que je viens de vous donner. Voilà où je veux en venir :

Validez la transformation quand vous la jugez correcte puis rétablissez l'opacité de l'appareil photo à 100%. Le travail est terminé, vous venez d'ajuster une image à l'échelle d'une autre  .
.

On a pu, ainsi, se rendre compte de la différence de taille entre l'appareil photo Konica (plus imposant) et l'appareil photo Minox (plus petit) grâce à la transformation en homothétie  .
.
Inclinaison
Ahhh, cette nouvelle transformation, elle va vous plaire, cela ne fait aucun doute ! Nous nous intéressons désormais à la transformation nommée Inclinaison.
Quand on clique dessus, nous n'avons à priori rien de nouveau. On retrouve notre espèce de cadre avec ses fameux petits carrés transparents. Ce qui change, c'est quand on manipule ces petits carrés.
Ici, il n'est plus réellement question de symétrie mais de redressement. Nous allons tout bonnement incliner le calque (pas difficile à deviner, je le conçois  ), c'est-à-dire que l'on va le pencher et pourquoi pas même le coucher.
), c'est-à-dire que l'on va le pencher et pourquoi pas même le coucher.
Un exemple arrive, n'hésitez pas à travailler avec moi ! Télécharger le fichier source Inclinaison.psd
Voici l'image sur laquelle je vais vous proposer d'effectuer une inclinaison.

Une fois la transformation Inclinaison choisie, on l'active :

En maintenant le clic sur le carré transparent situé en haut au milieu de l'image puis en déplaçant le curseur vers la droite, on remarque que le haut du calque se déplace en conséquence sans que le bas ne bouge.


En transformant l'image à partir d'un des carrés situés en son milieu (comprendre tous les carrés sauf ceux qui se situent dans les coins de l'image), on ne travaille que sur l'axe des abscisses ou l'axe des ordonnées. Sur cet exemple, nous avons travaillé sur l'axe des abscisses (nous avons effectué un transformation de gauche à droite). On remarque alors que le déplacement a été totalement linéaire (si nous avions cliqué sur le carré transparent situé au coin inférieur droite par exemple, nous aurions pu effectivement travailler sur l'axe des ordonnées et des abscisses car nous aurions pu effectuer un déplacement de haut en bas et de gauche à droite).
Continuons. Là, on peut déjà dire que l'image est inclinée, mais allons accentuer cette inclinaison en travaillant sur ce petit carré.

Je déplace alors ce carré vers le bas.

Je vous invite à comparer les deux dernières images. La différente n'est pas très importante, mais clairement visible. N'oubliez pas qu'il faut taper sur la touche Entrée de votre clavier (ou cliquer sur le bouton prévu à cet effet dans la barre des options) pour appliquer la transformation.
Pour le plaisir, j'ai ajouté une petite ombre portée à l'image pour lui donner un peu plus de style.

Qu'est-ce que cela donne si on transforme le calque à partir des coins de l'image ?
En travaillant avec les coins de l'image, l'inclinaison sera encore plus prononcée. Je dirais même que l'image sera couchée, on donnera l'impression qu'il existe un sol invisible sur lequel l'image s'est posée.
Je vous propose un petit essai, toujours sur la même image bien entendu.

Nous allons maintenir le clic sur le coin inférieur droite de l'image.

Puis, nous déplaçons notre curseur comme nous l'avons appris. On note encore une fois la linéarité sur les deux axes  .
.

On y ajoute un petite touche personnelle, et voilà le résultat  …
…

Plutôt sympa cet effet de perspective, n'est-ce pas ? 
Allez, on passe au tout dernier chapitre avant d'attaquer la deuxième partie. Courage ! 





