- Ada : Notions avancées et Programmation Orientée Objet
- Variables III : Gestion bas niveau des données
Lors du chapitre sur les tableaux (partie III), nous avions abordé l'algorithme de tri par sélection (Exercice 3). Cet algorithme consistait à trier un tableau d'entiers du plus petit au plus grand en comparant progressivement les éléments d'un tableau avec leurs successeurs, quitte à effectuer un échange (n'hésitez pas à relire cet exercice si besoin). Comme je vous l'avais alors dit, cet algorithme de tri est très rudimentaire et sa complexité était forte.
C'est quoi la complexité ? Comment peut-on mieux trier un tableau ?
Ce sont les deux questions auxquelles nous allons tenter de répondre. Nous commencerons par évoquer quelques algorithmes de tri (sans chercher à être exhaustif) : tri par sélection (rappel), tri à bulles, tri par insertion, tri rapide, tri fusion et tri par tas. Je vous expliquerai le principe avant de vous proposer un implémentation possible. Ensuite, nous expliquerons en quoi consiste la complexité d'un algorithme et aborderons les aspects mathématiques nécessaires de ce chapitre. Enfin, nous étudierons la complexité de ces différents algorithmes de manière empirique en effectuant quelques mesures.
Ce chapitre est davantage un chapitre d'algorithmique que de programmation. Aucune nouvelle notion de programmation ne sera abordée. En revanche, nous étudierons différentes techniques de tri, parfois surprenantes. Qui plus est, l'étude de complexité, si elle se veut empirique, fera toutefois appel à des notions mathématiques peut-être compliquées pour certains. Pour toutes ces raisons, ce chapitre n'est pas obligatoire pour la poursuite du cours.
- Algorithmes de tri lents
- Algorithmes de tri plus rapides
- Théorie : complexité d'un algorithme
- Mesures de complexité des algorithmes
Algorithmes de tri lents
De nombreux domaines, notamment scientifiques, ont besoin d'algorithmes efficaces : traitement du génome humain, météorologie, positionnement par satellite, opérations financières, calcul intensif… Ces domaines ne peuvent se permettre d'attendre des heures un résultat qui pourrait être obtenu en quelques minutes par de meilleurs algorithmes. Pour bien comprendre cette notion d'efficacité, commençons par évoquer des algorithmes de tris parmi les plus lents (cette notion de lenteur sera précisée et nuancée plus tard) : tri par sélection, tri par insertion et tri à bulles. Nous aurons par la suite besoin de quelques programmes essentiels : initialisation et affichage d'un tableau, échange de valeurs. Je vous fournis de nouveau le code nécessaire ci-dessous.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | function init return T_Tableau is T:T_Tableau ; subtype Intervalle is integer range 1..100 ; package Aleatoire is new Ada.numerics.discrete_random(Intervalle) ; use Aleatoire ; Hasard : generator ; begin Reset(Hasard) ; for i in T'range loop T(i) := random(Hasard) ; end loop ; return T ; end init ; --Afficher affiche les valeurs d'un tableau sur une même ligne procedure Afficher(T : T_Tableau) is begin for i in T'range loop Put(T(i),4) ; end loop ; end Afficher ; --Echanger est une procédure qui échange deux valeurs : a vaudra b et b vaudra a procedure Echanger(a : in out integer ; b : in out integer) is c : integer ; begin c := a ; a := b ; b := c ; end Echanger ; |
Tri par sélection (ou par extraction)
Principe
|
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|
|
7 |
3 |
18 |
13 |
7 |
Nous allons trier le tableau ci-dessus par sélection. Le principe est simple : nous allons chercher le minimum du tableau et l'échanger avec le premier élément :
Rang 1
|
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|
|
7 |
3 |
18 |
13 |
7 |
|
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|
|
3 |
7 |
18 |
13 |
7 |
Puis on réitère l'opération : on recherche le minimum du tableau (privé toutefois du premier élément) et on l'échange avec le second (ici pas d'échange nécessaire).
Rang 2
|
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|
|
3 |
7 |
18 |
13 |
7 |
On réitère à nouveau l'opération : on recherche le minimum du tableau (privé cette fois des deux premiers éléments) et on l'échange avec le troisième.
Rang 3
|
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|
|
3 |
7 |
18 |
13 |
7 |
|
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|
|
3 |
7 |
7 |
13 |
18 |
On réitère ensuite avec le quatrième élément et on obtient ainsi un tableau entièrement ordonné par ordre croissant. C'est l'un des algorithmes les plus simples et intuitifs. Pour aller plus loin ou pour davantage d'explications, vous pouvez consulter le tutoriel de K-Phoen à ce sujet (langage utilisé : C).
Mise en œuvre
Je vous fournis à nouveau le code source de l'algorithme de tri par sélection quelque peu modifié par rapport à la fois précédente :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | function RangMin(T : T_Tableau ; debut : integer ; fin : integer) return integer is Rang : integer := debut ; Min : integer := T(debut) ; begin for i in debut..fin loop if T(i)<Min then Min := T(i) ; Rang := i ; end if ; end loop ; return Rang ; end RangMin ; function Trier(Tab : T_Tableau) return T_Tableau is T : T_Tableau := Tab ; begin for i in T'range loop Echanger(T(i),T(RangMin(T,i,T'last))) ; end loop ; return T ; end Trier ; |
Tri par insertion
Principe
Le principe du tri par insertion est le principe utilisé par tout un chacun pour ranger ses cartes : on les classe au fur et à mesure. Imaginons que dans une main de 5 cartes, nous ayons déjà trié les trois premières, nous arrivons donc à la quatrième carte. Que fait-on ? Eh bien c'est simple, on la sort du paquet de cartes pour l'insérer à la bonne place dans la partie des cartes déjà triées. Exemple :
|
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|
|
5 |
9 |
10 |
6 |
7 |
|
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|
|
5 |
6 |
9 |
10 |
7 |
Il faudra ensuite s'occuper du cinquième élément mais là n'est pas la difficulté, car vous vous en doutez peut-être, mais il est impossible d'insérer un élément entre deux autres dans un tableau. Il n'y a pas de case n°1,5 ! Donc «réinsérer» le quatrième élément dans le tableau consistera en fait à décaler tous ceux qui lui sont supérieurs d'un cran vers la droite. Pour aller plus loin ou pour davantage d'explications, vous pouvez consulter le tutoriel de bluestorm à ce sujet (langage utilisé : C) et sa suite utilisant les listes (langage utilisé : OCaml).
Mise en œuvre
Je vous invite à rédiger cet algorithme par vous-même avant de consulter la solution que je vous propose, c'est la meilleure façon de savoir si vous avez compris le principe ou non (d'autant plus que cet algorithme est relativement simple).
1 2 3 4 5 6 7 8 9 10 11 | function tri_insertion(T : T_Tableau) return T_Tableau is Tab : T_Tableau := T ; begin for i in T'first + 1 .. T'last loop for j in reverse T'first + 1..i loop exit when Tab(j-1)<=Tab(j) ; echanger(Tab(j-1),Tab(j)) ; end loop ; end loop ; return Tab ; end Tri_insertion ; |
L'instruction EXIT située au cœur des deux boucles peut être remplacée par un IF :
1 2 3 4 | if Tab(j-1)<=Tab(j) then exit ; else echanger(Tab(j-1),Tab(j)) ; end if ; |
Tri à bulles (ou par propagation)
Principe
Voici enfin le plus «mauvais» algorithme. Comme les précédents il est plutôt intuitif mais n'est vraiment pas efficace. L'algorithme de tri par propagation consiste à inverser deux éléments successifs s'ils ne sont pas classés dans le bon ordre et à recommencer jusqu'à ce que l'on parcourt le tableau sans effectuer une seule inversion. Ainsi, un petit élément sera échangé plusieurs fois avec ses prédécesseurs jusqu'à atteindre son emplacement définitif : il va se propager peu à peu, ou «remonter» vers la bonne position lentement, comme une bulle d'air remonte peu à peu à la surface (j'ai l'âme d'un poète aujourd'hui  ).
).
Je ne pense pas qu'un exemple soit nécessaire. L'idée (simplissime) est donc de parcourir plusieurs fois le tableau jusqu'à obtenir la solution. Vous vous en doutez, cette méthode est assez peu évoluée et demandera de nombreux passages pour obtenir un tableau rangé. Pour aller plus loin ou pour davantage d'explications, vous pouvez consulter le tutoriel de shareman à ce sujet (langage utilisé : C++).
Mise en œuvre
Là encore, vous devriez être capable en prenant un peu de temps, de coder cet algorithme par vous-même.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | function Tri_Bulles(T : T_Tableau) return T_Tableau is Tab : T_Tableau := T ; Echange_effectue : boolean := true ; begin while Echange_effectue loop --possibilité d'afficher le tableau en écrivant ici --Afficher(Tab) ; Echange_effectue := false ; for i in Tab'first .. Tab'last-1 loop if Tab(i) > Tab(i+1) then echanger(Tab(i), Tab(i+1)) ; Echange_effectue := true ; end if ; end loop ; end loop ; return Tab ; end Tri_Bulles ; |
Si vous faites quelques essais en affichant Tab à chaque itération, vous vous rendrez vite compte qu'avec cet algorithme le plus grand élément du tableau est immédiatement propager à la fin du tableau dès le premier passage. Il serait donc plus judicieux de modifier les bornes de la deuxième boucle en écrivant :
1 | Tab'first .. Tab'last-1 - k |
Où k correspondrait au nombre de fois que le tableau a été parcouru. Autre amélioration possible : puisque les déplacements des grands éléments vers la droite se font plus vite que celui des petits vers la gauche (déplacement maximal de 1 vers la gauche), pourquoi ne pas changer de sens une fois sur deux : parcourir le tableau de gauche à droite, puis de droite à gauche, puis de gauche à droite… c'est ce que l'on appelle le Tri Cocktail (Shaker Sort), un poil plus efficace.
Enfin, une dernière amélioration mérite d'être signalée (mais non traitée), c'est le Combsort. Il s'agit d'un tri à bulles nettement amélioré puisqu'il peut rivaliser avec les meilleurs algorithmes de tri. L'idée, plutôt que de comparer des éléments successifs, est de comparer des éléments plus éloignés afin d'éviter les tortues, c'est-à-dire ces petits éléments qui ne se déplacent que d'un seul cran vers la gauche avec le tri à bulles classique. Ce cours n'ayant pas vocation à rédiger tous les algorithmes de tri possibles et imaginables, consultez le lien ci-dessus ou wikipedia pour en savoir plus.
Algorithmes de tri plus rapides
Tri rapide (ou Quick Sort)
Principe
L'algorithme de tri rapide (ou Quick Sort) a un fonctionnement fort différent des algorithmes précédents et un peu plus compliqué (certains diront beaucoup plus). Le principe de base est simple mais bizarre a priori : on choisit une valeur dans le tableau appelée pivot (nous prendrons ici la première valeur du tableau) et on déplace avant elle toutes celles qui lui sont inférieures et après elle toutes celles qui lui sont supérieures. Puis, on réitère le procédé avec la tranche de tableau inférieure et la tranche de tableau supérieure à ce pivot.
Voici un exemple :
|
13 |
18 |
9 |
15 |
7 |
Nous prenons le premier nombre en pivot : 13 et nous plaçons les nombres 9 et 7 avant le 13, les nombres 15 et 18 après le 13.
|
9 |
7 |
13 |
15 |
18 |
Il ne reste plus ensuite qu'à réitérer l'algorithme sur les deux sous-tableaux.
|
9 |
7 |
|
15 |
18 |
Le premier aura comme pivot 9 et sera réorganisé, le second aura comme pivot 15 et ne nécessitera aucune modification. Il restera alors deux sous-sous-tableaux.
|
7 |
|
18 |
Comme ces sous-sous-tableaux se résument à une seule valeur, l'algorithme s'arrêtera. Cet algorithme est donc récursif et l'une des difficultés est de répartir les valeurs de part et d'autre du nombre pivot. Revenons, à notre tableau initial. Nous allons chercher le premier nombre plus petit que 13 de gauche à droite avec une variable i, et le premier nombre plus grand que 13 de droite à gauche avec une variable j, jusqu'à ce que i et j se rencontrent.
|
13 |
18 |
9 |
15 |
7 |
On trouve 18 et 7. On les inverse et on continue.
|
13 |
7 |
9 |
15 |
18 |
Le rangement est presque fini, il ne reste plus qu'à inverser le pivot avec le 9.
|
9 |
7 |
13 |
15 |
18 |
Pour aller plus loin ou pour davantage d'explication, vous pouvez consulter le tutoriel de GUILOooo à ce sujet (langages utilisés : C et OCaml).
Mise en œuvre
Cet algorithme va être plus compliqué à mettre en œuvre. Je vous conseille d'essayer par vous-même afin de faciliter la compréhension de la solution que je vous fournis :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 | function tri_rapide (T : vecteur) return vecteur is procedure tri_rapide(T : in out vecteur ; premier,dernier : integer) is index_pivot : integer := (premier+dernier)/2 ; j : integer := premier + 1; begin if premier < dernier then echanger(T(premier),T(index_pivot)) ; index_pivot := premier ; for i in premier+1..dernier loop if T(i) < T(index_pivot) then echanger(T(i),T(j)) ; j := j +1 ; end if ; end loop ; echanger(T(index_pivot),T(j-1)) ; index_pivot := j-1 ; tri_rapide(T, premier, Index_pivot-1) ; tri_rapide(T, Index_pivot+1, dernier) ; end if ; end tri_rapide ; Tab : Vecteur := T ; begin tri_rapide(Tab,Tab'first,Tab'last) ; return Tab ; end tri_rapide ; |
Nous verrons un peu plus tard pourquoi j'ai du utiliser une procédure plutôt qu'une fonction pour effectuer ce tri.
Tri fusion (ou Merge Sort)
Principe
Ah ! Mon préféré. Le principe est simple mais rudement efficace (un peu moins que le tri rapide toutefois). Prenons le tableau ci-dessous :
|
8 |
5 |
13 |
7 |
10 |
L'idée est de «scinder» ce tableau en cinq cases disjointes que l'on va «refusionner» ensuite, mais dans le bon ordre. Par exemple, les deux premières cases, une fois refusionnées donneront :
|
5 |
8 |
Les deux suivantes donneront :
|
7 |
13 |
Et la dernière va rester seule pour l'instant. Ensuite, on va «refusionner» nos deux minitableaux (la dernière case restant encore seule) :
|
5 |
7 |
8 |
13 |
Et enfin, on fusionne ce dernier tableau avec la dernière case restée seule depuis le début :
|
5 |
7 |
8 |
10 |
13 |
Vous l'aurez compris, le tri se fait au moment de la fusion des sous-tableaux. L'idée n'est pas si compliquée à comprendre, mais un peu plus ardue à mettre en œuvre. En fait, nous allons créer une fonction tri_fusion qui sera récursive et qui s'appliquera à des tranches de tableaux (les deux moitiés de tableaux, puis les quatre moitiés de moitiés de tableaux, puis …) avant de les refusionner. Pour aller plus loin ou pour davantage d'explication, vous pouvez consulter le tutoriel de renO à ce sujet (langage utilisé : Python).
Mise en œuvre
Nous aurons besoin de deux fonctions pour effectuer le tri fusion : une fonction fusion qui fusionnera deux tableaux triés en un seul tableau trié ; et une fonction tri_fusion qui se chargera de scinder le tableau initial en sous-tableaux triés avant de les refusionner à l'aide de la précédente fonction.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 | function fusion(T1,T2 : Vecteur) return Vecteur is T : Vecteur(1..T1'length + T2'length) ; i : integer := T1'first ; j : integer := T2'first ; begin if T1'length = 0 then return T2 ; elsif T2'length = 0 then return T1 ; end if ; for k in T'range loop if i > T1'last and j > T2'last then exit ; elsif i > T1'last then T(k..T'last) := T2(j..T2'last) ; exit ; elsif j > T2'last then T(k..T'last) := T1(i..T1'last) ; exit ; end if ; if T1(i) <= T2(j) then T(k) := T1(i) ; i := i + 1 ; else T(k) := T2(j) ; j := j + 1 ; end if ; end loop ; return T ; end fusion ; FUNCTION Tri_fusion(T: Vecteur) RETURN Vecteur IS lg : constant Integer := T'length; BEGIN if lg <= 1 then return T ; else declare T1 : Vecteur(T'first..T'first-1+lg/2) ; T2 : Vecteur(T'first+lg/2..T'last) ; begin T1 := tri_fusion(T(T'first..T'first-1+lg/2)) ; T2 := tri_fusion(T(T'first+lg/2..T'last)) ; return fusion(T1,T2) ; end ; end if ; END Tri_Fusion; |
Tri par tas
Noms alternatifs
Le tri par tas porte également les noms suivants :
- Tri arbre
- Tri Maximier
- Heapsort
- Tri de Williams
Principe
|
5 |
7 |
3 |
8 |
12 |
6 |
L'idée du tri pas tas est de concevoir votre tableau tel un arbre. Par exemple, le tableau ci-dessus devra être vu ainsi :
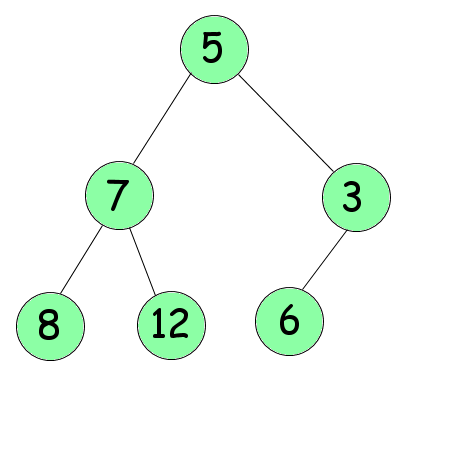
Chaque «case» de l'arbre est appelée nœud, le premier nœud porte le nom de racine, les derniers le nom de feuille. Si l'on est rendu au nœud numéro $n$ (indice dans le tableau initial), ses deux feuilles porteront les numéros $2n$ et $2n+1$.
L'arbre n'est pas trié pour autant. Pour cela nous devrons le tamiser, c'est-à-dire prendre un nombre et lui faire descendre l'arbre jusqu'à ce que les nombres en dessous lui soient inférieurs. Pour l'exemple, nous allons tamiser le premier nœud (le 5).
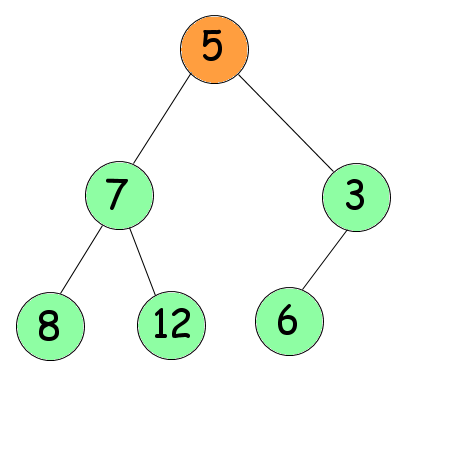
En dessous de lui se trouvent deux nœuds : 7 et 3. On choisit le plus grand des deux : 7. Comme 7 est plus grand que 5, on les inverse.
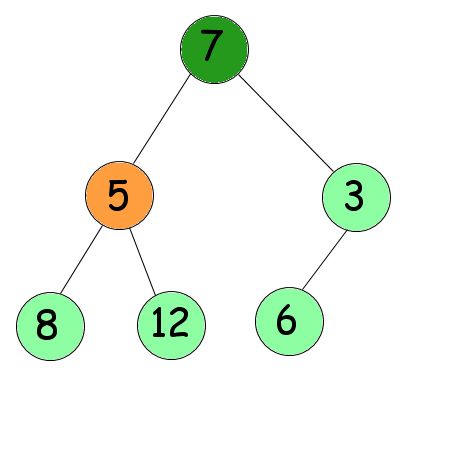
On recommence : les deux nœuds situés en dessous sont 8 et 12. Le plus grand est 12. Comme 12 est plus grand que 5, on les inverse.
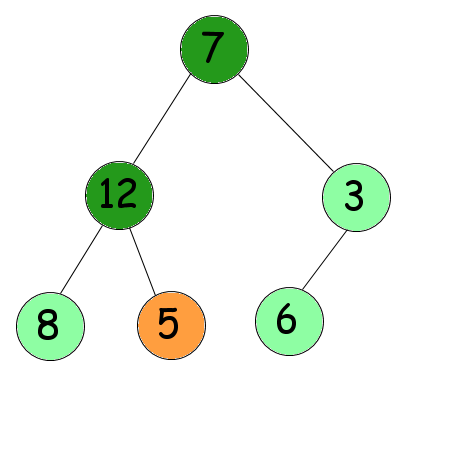
Vous avez compris le principe du tamisage ? Très bien. Pour trier notre arbre par tas, nous allons le tamiser en commençant, non pas par la racine de l'arbre, mais par les derniers nœuds (en commençant par la fin en quelque sorte). Bien sûr, il est inutile de tamiser les feuilles de l'arbre : elles ne descendront pas plus bas ! Pour limiter les tests inutiles, nous commencerons par tamiser le 3, puis le 7 et enfin le 5. Du coup, nous ne tamiserons que la moitié des nœuds de l'arbre. Faites l'essai, cela devrait vous donner ceci :
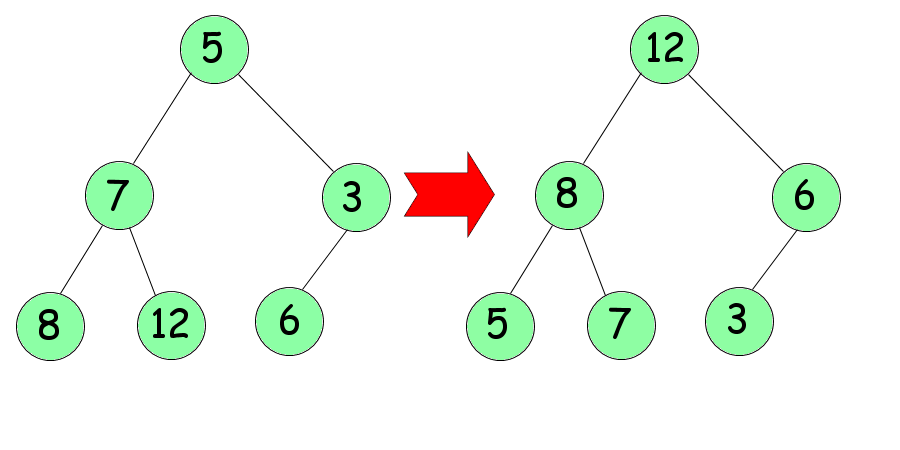
Hein ?!? Plus on descend dans l'arbre plus les nombres sont petits, mais c'est pas trié pour autant ?! 
En effet. Mais rassurez-vous, il reste encore une étape, un peu plus complexe. Nous allons parcourir notre arbre en sens inverse encore une fois. Nous allons échanger le dernier nœud de notre arbre tamisé (le 3) avec le premier (le 12) qui est également le plus grand nombre le l'arbre.
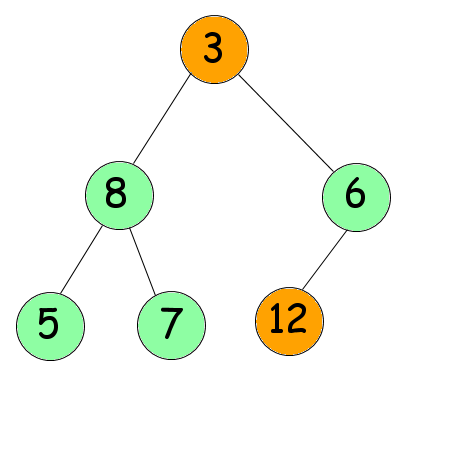
Une fois cet échange effectué, nous allons tamiser notre nouvelle racine, en considérant que la dernière feuille ne fait plus partie de l'arbre (elle est correctement placée désormais). Ce qui devrait nous donner le résultat suivant (voir la figure suivante).
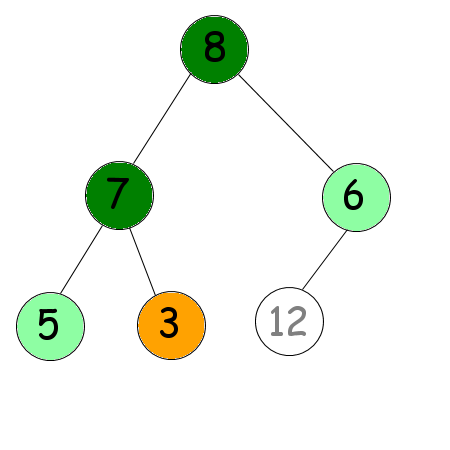
Cette manœuvre a ainsi pour but de placer sur la dernière feuille, le nombre le plus grand, tout en gardant un sous-arbre qui soit tamisé. Il faut ensuite répéter cette manœuvre avec l'avant-dernière feuille, puis l'avant-avant-dernière feuille… Jusqu'à arriver à la deuxième (et oui, inutile d'échanger la racine avec elle-même, soyons logique). Nous devrions ainsi obtenir le résultat suivant (voir la figure suivante).
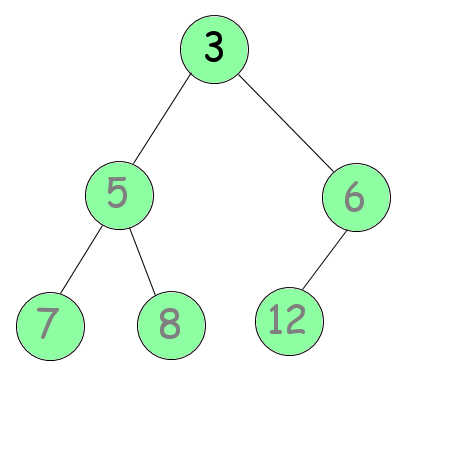
Cette fois, l'arbre est trié dans le bon ordre, l'algorithme est terminé. Il ne vous reste plus qu'à l'implémenter.
Mise en œuvre
Vous l'aurez deviné je l'espère, il nous faut une procédure tamiser, en plus de notre fonction Tri_tas. Commencez par la créer et l'essayer sur le premier élément comme nous l'avons fait dans cette section avant de vous lancer dans votre fonction de tri. Pensez qu'il doit être possible de limiter la portion de tableau à tamiser et que pour passer d'un nœud $n$ à celui du dessous, il faut multiplier $n$ par 2 (pour accéder au nœud en dessous à gauche) et éventuellement lui ajouter 1 (pour accéder à celui en dessous à droite).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | procedure tamiser(T : in out vecteur ; noeud : integer ; max : integer) is racine : integer := noeud ; feuille : integer := 2 * noeud ; begin while feuille <= max loop if feuille+1 <= max and then T(feuille)<T(feuille+1) then feuille := feuille + 1 ; end if ; if T(racine)<T(feuille) then echanger(T(racine), T(feuille)) ; end if ; racine := feuille ; feuille := 2 * racine ; end loop ; end tamiser ; function tri_tas(T : vecteur) return vecteur is Arbre : vecteur(1..T'length) := T ; begin for i in reverse 1..Arbre'length/2 loop tamiser(Arbre,i,Arbre'length) ; end loop ; for i in reverse 2..Arbre'last loop echanger(Arbre(i),Arbre(1)) ; tamiser(Arbre,1,i-1) ; end loop ; return Arbre ; end tri_tas ; |
Théorie : complexité d'un algorithme
Complexité
Si vous avez dors et déjà testé les programmes ci-dessus sur de grands tableaux, vous avez du vous rendre compte que certains étaient plus rapides que d'autres, plus efficaces. C'est ce que l'on appelle l'efficacité d'un algorithme. Pour la mesurer, la quantifier, on s'intéresse davantage à son contraire, la complexité. En effet, pour mesurer la complexité d'un algorithme il «suffit» de mesurer la quantité de ressources qu'il exige (mémoire ou temps-processeur).
En effet, le simple fait de déclarer un tableau exige de réquisitionner des emplacements mémoires qui seront rendus inutilisables par d'autres programmes comme votre système d'exploitation. Tester l'égalité entre deux variables va nécessiter de réquisitionner temporairement le processeur, le rendant très brièvement inutilisable pour toute autre chose. Vous comprenez alors que parcourir un tableau de 10 000 cases en testant chacune des cases exigera donc de réquisitionner au moins 10 000 emplacements mémoires et d'interrompre 10 000 fois le processeur pour faire nos tests. Tout cela ralentit les performances de l'ordinateur et peut même, pour des algorithmes mal ficelés, saturer la mémoire entraînant l'erreur STORAGE_ERROR : EXCEPTION_STACK_OVERFLOW.
D'où l'intérêt de pouvoir comparer la complexité de différents algorithmes pour ne conserver que les plus efficaces, voire même de prédire cette complexité. Prenons par exemple l'algorithme dont nous parlions précédemment (qui lit un tableau et teste chacune de ses cases) : si le tableau a 100 cases, l'algorithme effectuera 100 tests ; si le tableau à 5000 cases, l'algorithme effectuera 5000 tests ; si le tableau a $n$ cases, l'algorithme effectuera $n$ tests ! On dit que sa complexité est en $O(n)$.
L'écriture O
Ça veut dire quoi ce zéro ?
Ce n'est pas un zéro mais la lettre O ! Et $O(n)$ se lit «grand O de n». Cette notation mathématique signifie que la complexité de l'algorithme est proportionnelle à $n$ (le nombre d'éléments contenus dans le tableau). Autrement dit, la complexité vaut «grosso-modo» $n$.
C'est pas «grosso modo égal à n» ! C'est exactement égal à n ! 
Prenons un autre exemple : un algorithme qui parcourt lui aussi un tableau à $n$ éléments. Pour chaque case, il effectue deux tests : le nombre est-il positif ? Le nombre est-il pair ? Combien va-t-il effectuer de tests ? La réponse est simple : deux fois plus que le premier algorithme, c'est à dire $2 \times n$. Autrement dit, il est deux fois plus lent. Mais pour le mathématicien ou l'informaticien, ce facteur 2 n'a pas une importance aussi grande que cela, l'algorithme a toujours une complexité proportionnelle au premier, et donc en $O(n)$.
Mais alors tous les algorithmes ont une complexité en $O(n)$ si c'est comme ça ?!
Non, bien sûr. Un facteur 2, 3, 20… peut être considéré comme négligeable. En fait, tout facteur constant peut être considéré comme négligeable. Reprenons encore notre algorithme : il parcourt toujours un tableau à $n$ éléments, mais à chaque case du tableau, il reparcourt tout le tableau depuis le début pour savoir s'il n'y aurait pas une autre case ayant la même valeur. Combien va-t-il faire de tests ? Pour chaque case, il doit faire $n$ tests et comme il y a $n$ cases, il devra faire en tout $n \times n = n^2$ tests. Le facteur n'est cette fois pas constant ! On dira que cet algorithme a une complexité en $O(n^2)$ et, vous vous en doutez, ce n'est pas terrible du tout. Et pourtant, c'est la complexité de certains de nos algorithmes de tris ! 
Donc, vous devez commencer à comprendre qu'il est préférable d'avoir une complexité en $O(n)$ qu'en $O(n^2)$. Malheureusement pour nous, en règle général, il est impossible d'atteindre une complexité en $O(n)$ pour un algorithme de tri (sauf cas particulier comme avec un tableau déjà trié, et encore ça dépend des algorithmes  ). Un algorithme de tri aura une complexité optimale quand celle-ci sera en $O(n \times \ln(n))$.
). Un algorithme de tri aura une complexité optimale quand celle-ci sera en $O(n \times \ln(n))$.
Quelques fonctions mathématiques
Qu'est-ce que c'est encore que cette notation $\ln(n)$ ?
C'est une fonction mathématique que l'on appelle le logarithme népérien. Les logarithmes sont les fonctions mathématiques qui ont la croissance la plus faible (en fait elles croissent très très vite au début puis ralentissent par la suite). Inversement, les fonctions exponentielles sont celles qui ont la croissance la plus rapide (très très lentes au début puis de plus en plus rapide).
Mon but ici n'est pas de faire de vous des mathématiciens, encore moins d'expliquer en détail les notions de fonction ou de «grand O», mais pour que vous ayez une idée de ces différentes fonctions, de leur croissance et surtout des complexités associées, je vous en propose quelques-unes sur le graphique ci-dessous :
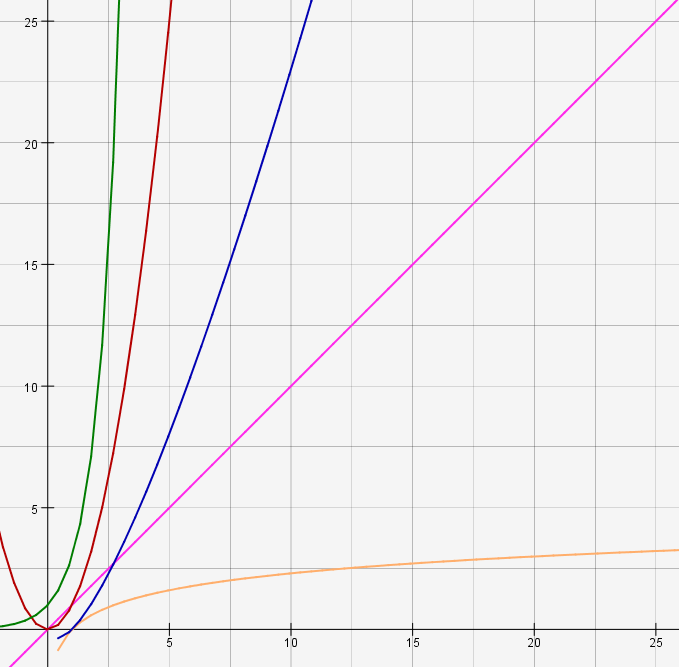
Légende :
Complexité en $O(e^n)$ (e : exponentielle)
Complexité en $O(n^2)$
Complexité en $O(n \times \log(n))$ (log : logarithme)
Complexité en $O(n)$
Complexité en $O(\log(n))$
Plus l'on va vers la droite, plus le nombre d'éléments à trier, tester, modifier… augmente. Plus l'on va vers le haut, plus le nombre d'opérations effectuées augmente et donc plus la quantité de mémoire ou le temps processeur nécessaire augmente. On voit ainsi qu'une complexité en $O(\log(n))$ ou $O(\ln(n))$, c'est peu ou prou pareil, serait parfaite (on parle de complexité logarithmique) : elle augmente beaucoup moins vite que le nombre d'éléments à trier ! Le rêve. Sauf que ça n'existe pas pour nos algorithmes de tri, donc oubliez-la.
Une complexité en $O(n)$ serait donc idéale (on parle de complexité linéaire). C'est possible dans des cas très particuliers : par exemple l'algorithme de tri par insertion peut atteindre une complexité en $O(n)$ lorsque le tableau est déjà trié ou «presque» trié, alors que les algorithmes de tri rapide ou fusion n'en sont pas capables. Mais dans la vie courante, il est rare que l'on demande de trier des tableaux déjà triés. 
On comprend donc qu'atteindre une complexité en $O(n \times \ln(n))$ est déjà satisfaisant (on parle de complexité linéarithmique), on dit alors que la complexité est asymptotiquement optimale, bref, on ne peut pas vraiment faire mieux dans la majorité des cas.
Une complexité en $O(n^2)$, dite complexité quadratique, est courante pour des algorithmes de tri simples (ou simplistes), mais très mauvaise. Si au départ elle ne diffère pas beaucoup d'une complexité linéaire (en $O(n)$), elle finit par augmenter très vite à mesure que le nombre d'éléments à trier augmente. Donc les algorithmes de tri de complexité quadratique seront réservés pour de petits tableaux.
Enfin, la complexité exponentielle (en $O(e^n)$) est la pire chose qui puisse vous arriver. La complexité augmente à vite grand V, de façon exponentielle (logique me direz-vous). N'ajoutez qu'un seul élément et vous aurez beaucoup plus d'opérations à effectuer. Pour un algorithme de tri, c'est le signe que vous coder comme un cochon.  Attention, les jugements émis ici ne concernent que les algorithmes de tri. Pour certains problèmes, vous serez heureux d'avoir une complexité en seulement $O(n^2)$.
Attention, les jugements émis ici ne concernent que les algorithmes de tri. Pour certains problèmes, vous serez heureux d'avoir une complexité en seulement $O(n^2)$.
Mesures de complexité des algorithmes
Un algorithme pour mesurer la complexité… des algorithmes
Après cette section très théorique, retournons à la pratique. Nous allons rédiger un programme qui va mesurer le temps d'exécution des différents algorithmes avec des tableaux de plus en plus grands. Ces temps seront enregistrés dans un fichier texte de manière à pouvoir ensuite transférer les résultats dans un tableur (Calc ou Excel par exemple) et dresser un graphique. Nous en déduirons ainsi, de manière empirique, la complexité des différents algorithmes. Pour ce faire, nous allons de nouveau faire appel au package Ada.Calendar et effectuer toute une batterie de tests à répétition avec nos divers algorithmes. Le principe du programme sera le suivant :
1 2 3 4 5 6 7 8 9 10 11 | POUR i ALLANT DE 1 A 100 REPETER | Créer Tableau Aléatoire de taille i*100 | Mesurer Tri_Selection(Tableau) | Mesurer Tri_Insertion(Tableau) | Mesurer Tri_Bulles(Tableau) | Mesurer Tri_Rapide(Tableau) | Mesurer Tri_Fusion(Tableau) | Mesurer Tri_Tas(Tableau) | Afficher "Tests effectués pour taille" i*100 | incrémenter i FIN BOUCLE |
La boucle devrait effectuer 100 tests, ce qui sera largement suffisant pour nos graphiques. Nous ne dépasserons pas des tableaux de taille 10 000 (les algorithmes lents devraient déjà mettre de 1 à 4 secondes pour effectuer leur tri), car au-delà, vous pourriez vous lasser. Par exemple, il m'a fallu 200s pour trier un tableau de taille 100 000 avec le tri par insertion et 743s avec le tri à bulles alors qu'il ne faut même pas une demi-seconde aux algorithmes rapides pour faire ce travail. Si vous le souhaitez, vous pourrez reprendre ce principe avec des tableaux plus importants pour les algorithmes plus rapides (vous pouvez facilement aller jusqu'à des tableaux de taille 1 million).
Mais que vont faire ces procédures ?
C'est simple, elles doivent :
- ouvrir un fichier texte ;
- lire "l'heure" ;
- exécuter l'algorithme de tri correspondant ;
- lire à nouveau "l'heure" pour en déduire la durée d'exécution ;
- enregistrer la durée obtenue dans le fichier ;
- fermer le fichier.
Cela impliquera de créer un type de pointeur sur les fonctions de tri. Voici le code source du programme :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 | procedure sort is type T_Ptr_Fonction is access function(T : Vecteur) return Vecteur ; type T_Tri is (SELECTION, INSERTION, BULLES, FUSION, RAPIDE, TAS) ; procedure mesurer(tri : T_Ptr_Fonction; T : Vecteur; choix : T_Tri) is temps : time ; duree : duration ; U :Vecteur(T'range) ; F : File_Type ; begin case choix is when SELECTION => open(F,Append_file,"./mesures/selection.txt") ; when INSERTION => open(F,Append_file,"./mesures/insertion.txt") ; when BULLES => open(F,Append_file,"./mesures/bulles.txt") ; when FUSION => open(F,Append_file,"./mesures/fusion.txt") ; when RAPIDE => open(F,Append_file,"./mesures/rapide.txt") ; when TAS => open(F,Append_file,"./mesures/tas.txt") ; end case ; temps := clock ; U := Tri(T) ; duree := clock - temps ; put(F,float(duree),Exp=>0) ; new_line(F) ; close(F) ; end mesurer ; tri : T_Ptr_Fonction ; F : File_Type ; begin create(F,Append_file,"./mesures/selection.txt") ; close(F) ; create(F,Append_file,"./mesures/insertion.txt") ; close(F) ; create(F,Append_file,"./mesures/bulles.txt") ; close(F) ; create(F,Append_file,"./mesures/fusion.txt") ; close(F) ; create(F,Append_file,"./mesures/rapide.txt") ; close(F) ; create(F,Append_file,"./mesures/tas.txt") ; close(F) ; for i in 1..100 loop declare T : Vecteur(1..i*100) ; begin generate(T,0,i*50) ; tri := Tri_select'access ; mesurer(tri,T,SELECTION) ; tri := Tri_insertion'access ; mesurer(tri,T,INSERTION) ; tri := Tri_bulles'access ; mesurer(tri,T,BULLES) ; tri := Tri_fusion'access ; mesurer(tri,T,FUSION) ; tri := Tri_rapide'access ; mesurer(tri,T,RAPIDE) ; tri := Tri_tas'access ; mesurer(tri,T,TAS) ; end ; put("Tests effectues pour la taille") ; put(i*100) ; new_line; end loop ; end sort ; |
L'exécution de ce programme nécessitera quelques minutes. Ne vous inquiétez pas si sa vitesse d'exécution ralentit au fur et à mesure : c'est normal puisque les tableaux sont de plus en plus lourds.
Traiter nos résultats
À l'aide du programme précédent, vous devez avoir obtenu six fichiers textes contenant chacun 100 valeurs décimales.
Et j'en fais quoi maintenant ? Je vais pas tout comparer à la main !
Bien sûr que non. Ouvrez donc un tableur (tel Excel ou Calc d'OpenOffice) et copiez-y les résultats obtenus. Sélectionnez les valeurs obtenues puis cliquez sur Insertion>Diagramme afin d'obtenir une représentation graphique des résultats obtenus. Je vous présente sur la figure suivante les résultats obtenus avec mon vieux PC.
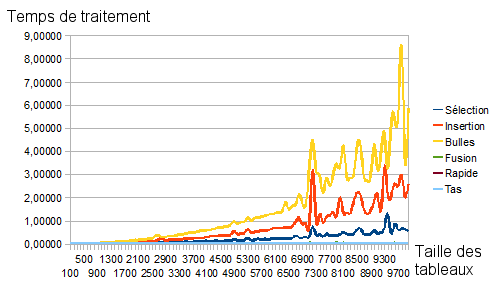
Avant même de comparer les performances de nos algorithmes, on peut remarquer une certaine irrégularité : des pics et des creux apparaissent et semblent (en général) avoir lieu pour tous les algorithmes. Ces pics et ces creux correspondent aux pires et aux meilleurs cas possibles. En effet, si notre programme de génération aléatoire de tableaux vient à créer un tableau quasi-trié, alors le temps mis par certains algorithmes chutera drastiquement. Inversement, certaines configurations peuvent être réellement problématiques à certains algorithmes : prenez un tableau quasi-trié mais dans le mauvais ordre ! Ce genre de tableau est catastrophique pour un algorithme de tri à bulles qui devra effectuer un nombre de passages excessif : il suffit, pour s'en convaincre, de regarder le dernier pic de la courbe jaune ci-dessus (tri à bulles) ; d'ailleurs ce pic est nettement atténué sur la courbe orange (tri par insertion) et quasi inexistant sur la courbe bleu (tri par sélection).
Qui plus est, il apparaît assez nettement que le temps de traitement des algorithmes rapides (tri rapide, tri fusion et tri par tas) est quasiment négligeable par rapport à celui des algorithmes lents (tri par insertion, tri par sélection et tri à bulles), au point que seuls ces derniers apparaissent sur le graphique.
Pour y voir plus clair, je vous propose de traiter nos chiffres avec un peu plus de finesse : nous allons distinguer les algorithmes lents des algorithmes rapides et nous allons lisser nos résultats. Par lisser, j'entends modifier nos résultats pour ne plus être gênés par ces pics et ces creux et voir apparaître une courbe plus agréable représentant la tendance de fond.
Lissage des résultats par moyenne mobile : Pour ceux qui se demanderaient ce qu'est ce lissage par moyenne mobile, voici une explication succincte (ce n'est pas un cours de statistiques non plus). Au lieu de traiter nos 100 nombres, nous allons créer une nouvelle liste de valeurs. La première valeur est obtenue en calculant la moyenne des 20 premiers nombres (du 1er au 20ème), la seconde est obtenu en calculant la moyenne des nombres entre le 2nd et le 21ème, la troisième valeur est obtenue en calculant la moyenne des nombres entre le 3ème et le 22ème… La nouvelle liste de valeurs est ainsi plus homogène mais aussi plus courte (il manquera 20 valeurs).
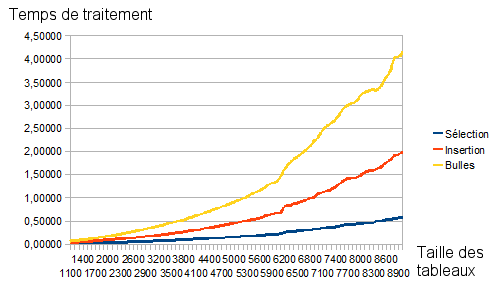
Algorithmes lents
Algorithmes rapides
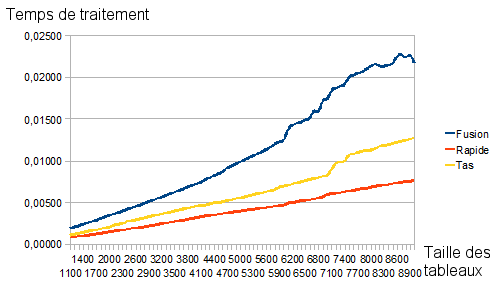
Ainsi retravaillés, nos résultats sont plus lisibles et on voit apparaître qu'en moyenne, l'algorithme le plus efficace est le tri rapide, puis viennent le tri par tas et le tri fusion. Mais même le tri fusion reste, en moyenne, en dessous de 0,025 seconde pour un tableau à 10 000 éléments sur mon vieil ordinateur (son score est sûrement encore meilleur chez vous), ce qui est très très loin des performances des trois autres algorithmes. Pour les trois plus lents, on remarque que le «pire» d'entre eux est, en moyenne, le tri à bulles, puis viennent le tri par insertion et le tri par sélection (avec des écarts de performance toutefois très nets entre eux trois).
Le lissage par moyenne mobile nous permet également de voir se dégager une tendance, une courbe théorique débarrassées des impuretés (pire cas et meilleur cas). Si l'on considère les algorithmes lents, on distingue un début de courbe en U, même si le U semble très écrasé par l'algorithme de tri par sélection. Cela nous fait donc penser à une complexité en $O(n^2)$ où n est le nombre d'éléments du tableau.
Et pourquoi pas en $\color{blue}{O(e^n)}$ ?
Prenez un tableau à $n$ éléments que l'on voudrait trier avec le pire algorithme : le tri à bulles. Dans le pire des cas, le tableau est trié en sens inverse et le plus petit élément est donc situé à la fin. Et comme le tri à bulle ne déplace le plus petit élément que d'un seul cran à chaque passage, il faudra donc effectuer $n-1$ passages pour que ce minimum soit à sa place et le tableau trié. De plus, à chaque itération, l'algorithme doit effectuer $n-1$ comparaison (et au plus $n-1$ échanges). D'où un total de $(n-1) \times (n-1)$ comparaisons. Or, $(n-1) \times (n-1) = n^2 -2 \times n + 1$, donc la complexité est « de l'ordre de » $n^2$. Dans le pire cas, l'algorithme de tri à bulles a une complexité en $O(n^2)$. Cette famille d'algorithme a donc une complexité quadratique et non exponentielle.
Considérons maintenant nos trois algorithmes rapides, leur temps d'exécution est parfaitement négligeable à côté des trois précédents, leurs courbes croissent peu : certaines semblent presque être des droites. Mais ne vous y trompez pas, leur complexité n'est sûrement pas linéaire, ce serait trop beau. Elle est toutefois linéarithmique c'est-à-dire en $O(n \times ln(n))$. Ces trois algorithmes sont donc asymptotiquement optimaux.
Différentes variantes de ces algorithmes existent. Les qualificatifs de «lent», «rapide», «pire» ou «meilleur» sont donc à prendre avec des pincettes, car certains peuvent être très nettement améliorés ou sont très utiles dans des cas particuliers.
Par exemple, notre algorithme de tri fusion est un tri en place : nous n'avons pas créer de second tableau pour effectuer notre tri afin d'économiser la mémoire, denrée rare si l'on trie de très grands tableaux (plusieurs centaines de millions de cases). Une variante consiste à ne pas l'effectuer en place : on crée alors un second tableau et l'opération de fusion gagne en rapidité. Dans ce cas, l'algorithme de tri fusion acquièrent une complexité comparable à celle du tri rapide en réalisant moins de comparaisons, mais devient gourmande en mémoire.
De la même manière, nous avons évoqué le Combsort qui est une amélioration du tri à bulles et qui permet à notre «pire» algorithme de côtoyer les performances des «meilleurs». Encore un dernier exemple, le «lent» algorithme de tri par insertion atteint une complexité linéaire en $O(n)$ sur des tableaux quasi-triés alors que l'algorithme de tri rapide garde sa complexité linéarithmique en $O(n \times ln(n))$.
En résumé :
- L'Algorithmique constitue une branche, peut-être la plus complexe, des Mathématiques et de l'Informatique.
- Vous devez donc vous interroger sur l'efficacité des algorithmes que vous rédigez.
- Effectuez des essais grandeur nature avec de grandes quantités de données et comptez le nombre d'opérations et de tests nécessaires pour juger de la pertinence de votre méthode.