Un jour, si êtes amenés à programmer des jeux vidéo, vous allez devoir vous intéresser à la notion de collisions. Vous souhaiterez alors savoir si votre voiture quitte la route, si un objet sort du cadre de la scène, si deux billes se touchent, ou encore si votre personnage a les pieds sur terre…
Au cours de ce chapitre, nous découvrirons ensemble les prémices de la théorie des collisions. Ainsi, nous serons capables de détecter une collision entre des objets de différentes tailles et différentes formes. Nous verrons également comment affiner, plus ou moins, cette détection de collisions, en fonction de la forme des objets, afin d'optimiser au maximum les performances du programme.
À la fin de ce chapitre, vous serez enfin en mesure de réaliser vos propres jeux vidéo !
Préambule
Définition d'une collision
Comme cela a été dit en introduction, nous parlerons de collisions tout au long de ce chapitre. Aussi, pour mieux comprendre tout ce qui va suivre, nous allons redéfinir proprement le terme « collision ».
Dans la vie de tous les jours, nous attribuons ce terme à toutes sortes d'impact ou de choc entre deux objets. Nous pouvons alors citer l'exemple d'un verre qui se brise au contact du sol, d'une balle qui atteint sa cible, ou encore d'une voiture qui percute un mur.
Dans un programme, nous pourrons parler de collision lorsque deux objets « se touchent » ou se chevauchent. De la même manière, nous pourrons savoir si un objet verre est en contact avec un autre objet sol, ou si notre objet voiture percute l'objet mur.
De base, rien n'empêche votre objet voiture de continuer sa course à travers l'objet mur. Cela ne posera absolument aucun problème à votre application pour continuer à s'exécuter. Il faut avouer que c'est tout de même fâchant !
Il nous incombe donc de gérer les collisions à l'intérieur de notre programme, afin de pouvoir exécuter des tâches appropriées.
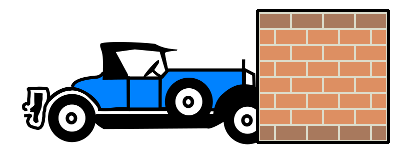
À la figure suivante, vous pouvez voir que les objets voiture et mur se chevauchent légèrement, et sont par conséquent en collision.
Détecter des collisions
Des fonctions booléennes
Le principal objectif pour un programmeur, sera donc de détecter l'existence ou non d'une collision entre deux objets.
Mais alors, comment savoir s'il y a collision entre deux objets ?
C'est justement toute la difficulté de la chose, mais également la raison d'être de ce chapitre. Nous verrons qu'il existe différents moyens d'y arriver, qui dépendent principalement de la forme des objets et de la précision souhaitée.
Quoi qu'il en soit, la détection de collisions se fera toujours de la même manière en Actionscript, comme dans les autres langages. Le principe est d'utiliser diverses fonctions ou méthodes, prenant en paramètres les objets à tester, et renvoyant un booléen. Ce booléen représentera alors l'existence ou non d'une collision entre les objets transmis.
L'intégralité de la gestion des collisions s'appuiera donc uniquement sur ces fonctions.
Effets produits par une collision
Les effets engendrés par une éventuelle collision, ne sont pas pris en compte dans ces fonctions de détection de collisions. Ce n'est qu'une fois la collision confirmée qu'il est possible de gérer l'impact généré par celle-ci.
Prenons l'exemple d'un choc entre deux boules quelconques, comme sur la figure suivante.

Dans l'exemple précédent, nous voyons que nos boules sont en collision à la troisième position. À la suite de ce choc, les boules sont alors déviées et leur vitesse modifiée. Dans ce cas précis, nous pourrions nous appuyer sur la théorie des chocs élastiques pour mettre à jour le mouvement de chacune des boules. Néanmoins l'effet produit par la collision aurait été traitée différemment s'il s'agissait d'un choc entre un objet voiture et un objet mur, ou encore entre les objets verre et sol.
Les instructions qui découlent d'une collision sont donc directement liés aux types d'objets que vous manipulez, ou plutôt à ce qu'ils représentent. Par ailleurs, cela dépend également de ce que vous, en tant que programmeur, souhaitez faire. Par exemple, l'impact de l'objet voiture sur le mur pourrait stopper net cette dernière en déformant son capot, mais pourrait tout aussi bien la faire « rebondir » et laisser celle-ci intacte. De plus, suivant la vue utilisée (vue de face, de dessus, de côté, etc.) et la manière dont vos classes sont construites, les instructions ne seraient pas tout les mêmes.
Les manipulations post-collision sont spécifiques à chaque programme, et ne sont pas forcément transposables pour tous vos projets. Dans ce chapitre, nous nous donc concentrerons uniquement sur les méthodes de détection de collisions entre objets.
La théorie des collisions
Collisions rectangulaires
La méthode hitTestObject()
Par défaut, tout objet héritant de DisplayObject dispose de deux méthodes servant à détecter des collisions entre objets d'affichage. La première, nommée hitTestObject(), est celle dont nous allons parler maintenant. Mais pour cela, nous aurons besoin de deux objets.
Traçons deux rectangles qui se superposent, au moins partiellement :
1 2 3 4 5 6 7 8 | var obj1:Shape = new Shape(); obj1.graphics.beginFill(0x000000); obj1.graphics.drawRect(0, 0, 100, 100); var obj2:Shape = new Shape(); obj2.graphics.beginFill(0x880088); obj2.graphics.drawRect(50, 50, 100, 100); addChild(obj1); addChild(obj2); |
La figure suivante nous confirme que les objets obj1 et obj2 se chevauchent bien.

À présent testons la collision entre ces deux objets.
Pour cela, nous allons donc nous servir de la méthode hitTestObject(), qui prend en paramètre, simplement l'objet d'affichage avec lequel tester la collision. Sachant que la méthode hitTestObject() appartient à la classe DisplayObject, nous pouvons aussi bien l'utiliser à partir de l'objet d'affichage obj1 comme obj2.
Pour s'assurer de son bon fonctionnement, affichons le résultat de cette fonction dans la console, comme ceci :
1 | trace(obj1.hitTestObject(obj2)); // Affiche : true |
Comme vous n'êtes pas dupes, confirmons le bon fonctionnement de la méthode hitTestObject(), en déplaçant un de des rectangles et en ré-affichant le résultat :
1 2 | obj2.y = 100; trace(obj1.hitTestObject(obj2)); // Affiche : false |
La méthode hitTestObject() possède néanmoins un énorme défaut lorsqu'il s'agit d'étudier un collision entre deux objets non rectangulaires. En effet, la détection de collision réalisée à l'intérieur de cette méthode est réalisée non pas sur les objets d'affichages eux-mêmes, mais sur leur cadre de sélection, dont nous allons parler maintenant.
Les cadres de sélection
Un cadre de sélection (ou bounding box en anglais) peut être défini comma la plus petite zone rectangulaire incluant intégralement un objet d'affichage.
Étant donné qu'un dessin est toujours plus parlant, reprenons l'exemple de la collision entre nos objets d'affichage voiture et mur. La figure suivante nous montre alors ces deux objets délimités par leur cadre de sélection respectif.
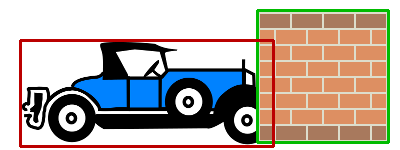
La classe DisplayObject dispose des deux méthodes getBounds() et getRect() pour récupérer les coordonnées du cadre de sélection d'un objet d'affichage. La différence entre celles-ci est que la méthode getRect() définit le cadre de sélection sans tenir compte des lignes contenues dans l'objet d'affichage. Pour plus d'informations, je vous invite à visiter cette page.
Pour revenir aux collisions rectangulaires, la méthode hitTestObject() réalise donc un test de collision entre les cadres de sélection de deux objets d'affichage, et non sur leurs formes réelles.
Ce type de collisions peut être donc être utile pour tout objet de forme rectangulaire, bien entendu, mais pas que ! La méthode hitTestObject() peut aussi vous servir lorsque vous n'avez pas besoin d'une précision extrême. Et enfin, les détections de collisions rectangulaires peuvent également être suffisante lorsque vos objets non rectangulaires sont de tailles minimes. En effet, pour des objets très petits, le cadre de sélection est quasiment confondu avec l'objet lui-même.
Collisions avec la scène principale
Jusqu'à présent, nous avons vu uniquement comment détecter des collisions rectangulaires correspondant, plus ou moins, à deux objets qui se percutent. Toutefois dans d'autres cas, il peut être utile de détecter si un objet sort d'une certaine zone délimitée.
Par exemple, ce type de collisions peut être utilisé pour détecter si un objet sort de la scène principale. Nous allons donc voir maintenant comment gérer ce genre de cas.
Sur la figure suivante, j'ai rappelé les coordonnées limites de la scène principale de votre animation.
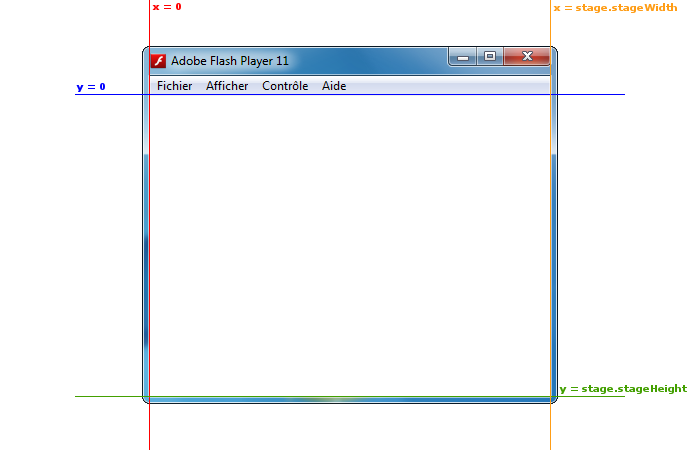
Pour apprendre à gérer les collision avec la scène principale, je vous propose un petit exemple. Nous allons ainsi réaliser une animation, où un rectangle suivra les mouvements de souris, mais sans sortir du cadre de la scène principale.
Commençons par dessiner un rectangle et faisons-le suivre la souris. Vous devriez maintenant savoir coder tout ça, mais je vais quand même vous donner de quoi suivre au cas où :
1 2 3 4 5 6 7 8 9 10 | var rectangle:Shape = new Shape(); rectangle.graphics.beginFill(0x00BB00); rectangle.graphics.drawRect(-50, -50, 100, 100); addChild(rectangle); stage.addEventListener(MouseEvent.MOUSE_MOVE, deplacer); function deplacer(event:MouseEvent):void { rectangle.x = event.stageX; rectangle.y = event.stageY; } |
Pour tester si notre objet sort de la scène principale, nous devons tester les limites de notre rectangle par rapport aux dimensions de l'animation. Étant donné que notre rectangle est centré sur son origine locale, nous pouvons détecter les dépassements de cette manière :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | function deplacer(event:MouseEvent):void { rectangle.x = event.stageX; rectangle.y = event.stageY; if (rectangle.x - rectangle.width / 2 < 0) { trace("Trop à gauche"); } if (rectangle.y - rectangle.height / 2 < 0) { trace("Trop haut"); } if (rectangle.x + rectangle.width / 2 > stage.stageWidth) { trace("Trop à droite"); } if (rectangle.y + rectangle.height / 2 > stage.stageHeight) { trace("Trop bas"); } } |
Certains d'entre vous pourriez vous dire qu'ici nous n'avons pas de fonction booléenne pour la détection de collisions. Toutefois, dois-je vous rappeler d'une condition renvoie une valeur booléenne ? Nous pouvons ainsi considérer chaque condition comme une détecter de collision avec une bordure. Dans cet exemple, Nous avons donc quatre tests de collisions différents ; évidemment, puisqu'un rectangle compte quatre côtés !
Enfin, pour empêcher le rectangle de sortir de la scène principale, il suffit de réinitialiser sa position pour que celui-ci reste adjacent à la bordure éventuellement franchie.
Voilà comment nous pourrions faire :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | function deplacer(event:MouseEvent):void { rectangle.x = event.stageX; rectangle.y = event.stageY; if (rectangle.x - rectangle.width / 2 < 0) { rectangle.x = rectangle.width / 2; } if (rectangle.y - rectangle.height / 2 < 0) { rectangle.y = rectangle.height / 2; } if (rectangle.x + rectangle.width / 2 > stage.stageWidth) { rectangle.x = stage.stageWidth - rectangle.width / 2; } if (rectangle.y + rectangle.height / 2 > stage.stageHeight) { rectangle.y = stage.stageHeight - rectangle.height / 2; } } |
Ici, nous avons travaillé avec la scène principale, néanmoins il est tout à fait possible de travailler avec un conteneur enfant de type Sprite. Il faudrait alors utiliser l'espace de coordonnées local à ce conteneur, ainsi que ses dimensions décrites par les attributs width et height. Pour généraliser ceci, quelque soit la position du rectangle par rapport à sa propre origine, il est possible d'utiliser la méthode getBounds() de l'objet en question.
Collisions circulaires
Le théorème de Pythagore
Pour détecter des collisions entre deux objets de forme circulaire, nous aurons besoin de calculer la distance qui sépare leur centre. Pour cela, nous utiliserons le théorème de Pythagore ! Certains d'entre vous auront peut-être l'impression de retourner sur les bancs de l'école, mais il est important de faire un petit rappel sur ce théorème. Je passerai néanmoins relativement vite sur ce point.
Pour rappel, le théorème de Pythagore définit une relation entre les trois côtés d'un triangle rectangle, tel que celui illustrer sur la figure suivante.
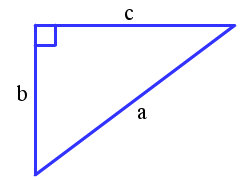
En utilisant la notation de l'image précédente, le théorème de Pythagore définit la relation suivante :
$\[a^2 = b^2 + c^2\]$
D'un point de vue littéraire, ce théorème est définit de la manière suivante : « si un triangle est rectangle, alors le carré de l’hypoténuse est égale à la somme des carrés des deux autres côtés ».
Calcul des distances
Maintenant, nous allons voir comment calculer la distance entre deux objets. Dans le cas présent, nous nous focaliserons sur les cercles. Néanmoins ceci peut facilement être transposables à d'autres types d'objets.
Lorsque nous utilisons le terme « distance » entre deux objets, nous parlons de celle qui sépare les centres de nos objets. Ainsi, à la figure suivante, nous pouvons voir comment elle est défini dans le cas des cercles.
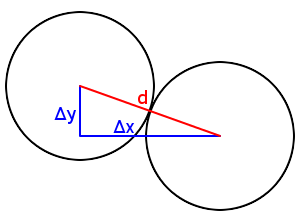
D'après le théorème de Pythagore, nous avons donc la relation suivante :
$\[d^2 = (\Delta x)^2 + (\Delta y)^2\]$
Dans l'expression précédente, $\Delta x$ représente la différence d'abscisse entre les deux objets, c'est-à-dire $\[x_2 - x_1\]$. Bien entendu, c'est la même chose pour $y$.
Nous supposerons ici que les objets d'affichage correspondant aux cercles, possèdent leur origine d'affichage au centre des cercles. Nous pouvons alors calculer la distance entre deux cercles de cette manière :
1 | var d:Number = Math.sqrt(Math.pow(objet2.x - objet1.x, 2) + Math.pow(objet2.y - objet1.y, 2)); |
Toutefois, en considérant le temps nécessaire pour réaliser cette opération, il serait préférable d'utiliser quelque chose de plus optimisé. En effet, l'utilisation de la multiplication est plus rapide que le passage par la méthode pow() de la classe Math. En fait, il serait plus intéressant, du point de vue des performances, de ne pas utiliser cette classe. C'est pourquoi, il est préférable de travailler avec des distances au carré, ce qui nous évite d'avoir recours à la méthode sqrt().
Voici donc comment redéfinir cette même instruction sans utiliser la classe Math et en restant en distance au carré :
1 | var d:Number = (objet2.x - objet1.x)*(objet2.x - objet1.x) + (objet2.y - objet1.y)*(objet2.y - objet1.y); |
Je rappelle qu'un carré est une valeur toujours positive. Quel que soit les objets et le sens dont vous les utilisez, le résultat sera toujours le même.
Détecter une collision
À présent, vous savez calculer la distance entre deux cercles. Cela tombe bien, nous allons justement en avoir besoin pour détecter les collisions entre objets de forme circulaire. Quelle que soit la position et l'orientation de chacun des deux cercles, ceux-ci seront en collision si la distance entre leur centre est inférieure à une certaine valeur. Voyez plutôt la figure suivante.
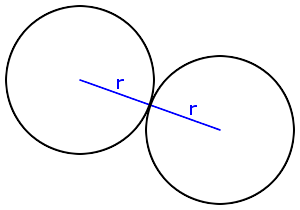
En regardant l'image précédente de plus près, nous pouvons en déduire que la distance maximale de collision entre deux cercles est $r_1 + r_2$, soit $2r$ dans le cas de deux cercles de rayons identiques. Par ailleurs, nous pouvons également utiliser le fait que le rayon d'un objet correspond exactement à la moitié de sa largeur ou de sa hauteur.
Pour détecter une collision entre deux objets d'affichage obj1 et obj2 de formes circulaires, nous pouvons définir une fonction de ce style :
1 2 3 4 5 6 7 8 9 | function testerCollision(obj1:DisplayObject, obj2:DisplayObject):Boolean { var collision:Boolean = false; var d:Number = (obj2.x - obj1.x)*(obj2.x - obj1.x) + (obj2.y - obj1.y)*(obj2.y - obj1.y); if(d < (obj1.width/2 + obj2.height/2)*(obj1.width/2 + obj2.height/2)){ collision = true; } return collision; } |
Encore une fois, ce code se base sur le fait que les objets d'affichage sont centrés sur leur origine. Si ce n'est pas le cas, il sera nécessaire de l'adapter légèrement.
Collisions ponctuelles
La méthode hitTestPoint()
Nous allons maintenant nous pencher sur le cas des collisions ponctuelles, c'est-à-dire entre un objet d'affichage et un point. Ce dernier sera alors uniquement caractérisé par ses coordonnées x et y.
Ici, nous n'allons pas faire de théorie, mais je vais plutôt vous présenter une méthode faisant le travail à votre place. Il s'agit de la méthode hitTestPoint() présente dans toute classe héritant de DisplayObject. En voici sa signature :
1 | hitTestPoint(x:Number, y:Number, shapeFlag:Boolean = false):Boolean |
Comme vous le voyez, l'utilisation de cette méthode nécessite de renseigner les coordonnées du point avec lequel tester la collision, ainsi d'un troisième paramètre facultatif nommée shapeFlag. Ce dernier paramètre, de type Boolean, sert à spécifier si la détection de collision doit être faite sur l'objet lui-même en tant que forme complexe (true) ou uniquement d'après son cadre de sélection (false).
Ce type de détections de collisions peut être extrêmement précieux dans certains cas. Par exemple, vous pourriez réaliser un jeu de tir et détecter la collision entre la position de votre curseur et un ennemi quelconque, comme l'illustre bien la figure suivante.
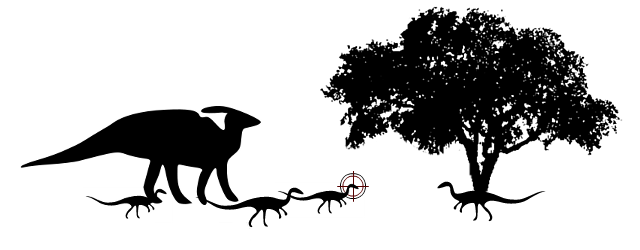
Pour vous donner un exemple de code, voici comment il serait possible de réaliser cette détection à partir de la méthode hitTestPoint() :
1 2 3 4 5 6 7 | stage.addEventListener(MouseEvent.MOUSE_DOWN, tir); function tir(event:MouseEvent):void { if (maCible.hitTestPoint(event.stageX, event.stageY, true)) { trace("Cible atteinte"); } } |
Si vous souhaitez tester ce code, il vous suffit d'instancier un objet d'affichage maCible et de l'ajouter à la liste d'affichage. Le code précédent vous servira alors à détecter les collisions entre votre curseur et cet objet, lors d'un clic avec votre souris.
Exercice : Un mini-jeu de tir
Le principe du jeu va être relativement simple. Nous allons tout d'abord dessiner un cercle à l'écran, qui baladera à l'intérieur de la scène principale. Puis lorsque vous cliquerez dessus, votre score de points augmentera.
Démarrons tout de suite en dessinant un disque que nous placerons initialement au centre de l'écran :
1 2 3 4 5 6 7 | var cible:Shape = new Shape(); cible.graphics.beginFill(0x880088); cible.graphics.drawCircle(0, 0, 50); cible.x = stage.stageWidth / 2; cible.y = stage.stageHeight / 2; addChild(cible); var score:int = 0; |
Pour gérer les mouvements de notre objet d'affichage, nous allons avoir besoin d'utiliser deux variables vitesseX et vitesseY qui représenteront donc, plus ou moins, un vecteur vitesse. Pour détecter les collisions avec la scène principale, nous utiliserons le principe des collisions rectangulaires, qui dans ce cas sera plus que suffisant. À la suite d'une collision, nous pourrons mettre à jour la position de l'objet ainsi que sa vitesse, qui sera inversée suivant la composante normale à la collision.
Tout ceci peut sans doute vous paraître compliqué, pourtant, regardez le code correspondant qui n'est pas si terrible :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | var vitesseX:int = 1 + Math.random() * 10; var vitesseY:int = 1 + Math.random() * 10; addEventListener(Event.ENTER_FRAME, deplacer); function deplacer(event:Event):void { cible.x += vitesseX; cible.y += vitesseY; if (cible.x - cible.width / 2 < 0) { cible.x = cible.width / 2; vitesseX = - vitesseX; } if (cible.y - cible.height / 2 < 0) { cible.y = cible.height / 2; vitesseY = - vitesseY; } if (cible.x + cible.width / 2 > stage.stageWidth) { cible.x = stage.stageWidth - cible.width / 2; vitesseX = - vitesseX; } if (cible.y + cible.height / 2 > stage.stageHeight) { cible.y = stage.stageHeight - cible.height / 2; vitesseY = - vitesseY; } } |
Enfin, la gestion des tirs peut se faire à l'aide la méthode hitTestpoint(), comme cela a été décrit précédemment :
1 2 3 4 5 6 7 8 9 | stage.addEventListener(MouseEvent.CLICK, tir); function tir(event:MouseEvent):void { if (cible.hitTestPoint(event.stageX, event.stageY, true)) { score += 10; trace("Score : " + score); } } |
L'exercice que nous venons de réaliser est un préambule à un jeu de tir plus complexe. Cependant, la plus grosse difficulté qu'est l'interaction est plutôt bien entamée. Pour vous exercer, je vous invite donc grandement à essayer de réaliser un vrai jeu de tir suivant vos envies.
Les collisions de pixels
Utiliser l'opacité
Les masques
Une autre manière d'appréhender les collisions, est d'utiliser les objets d'affichage sous forme d'images bitmap. Comme vous le savez maintenant, ces images sont décrites par une série de pixels. Et rappelez-vous, les pixels sont caractérisés par des nombres de la forme 0xAARRVVBB, où AA représentent l'opacité du pixel.
L'opacité d'un objet d'affichage permet justement de décrire les contours de la partie visible de celui-ci. C'est pourquoi l'opacité est grandement utile pour effectuer des tests de collisions. Mais nous reviendrons là-dessus plus tard.
En attendant, la figure suivante vous montre à quoi peut ressembler le canal alpha de l'image voiture, appelé généralement masque de l'image.
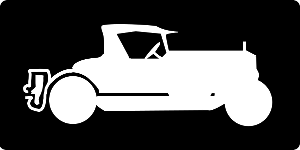
Bien entendu, il serait tout à fait possible de réaliser des tests de collisions en utilisant les canaux rouge, vert ou bleu. Cependant, cela n'est pas très courant, aussi, nous n'en parlerons pas.
Une manière de détecter des collisions
Ici, nous allons voir comment nous pourrions procéder pour détecter une collision entre deux images bitmap. Toutefois, nous verrons que la classe BitmapData intègre une méthode hitTest(). Malheureusement je ne suis pas certain de son fonctionnement interne. Mais quoi qu'il en soit, cela ne nous empêche pas d'imaginer une manière dont cela pourrait être fait.
La technique dont je vais vous parler est simplement tirée de mon imagination. Il est donc fort probable qu'il y ait d'autres manières d'y parvenir, et de façon plus optimisée. Néanmoins, je cherche ici simplement à vous faire découvrir une méthode que vous pourriez vous-mêmes transcrire en code. Vous pourrez ensuite très facilement adapter celle-ci ou une autre à vos projets, pour des applications diverses.
La technique que je vais vous présenter maintenant, tire parti du fait qu'une transparence totale est représentée par une valeur correspondante nulle. Également, je ferais l'hypothèse que l'opacité est représentée par une valeur décimale comprise entre 0 et 1. Ainsi, en multipliant simplement les valeurs des opacités des deux pixels devant se superposer, nous obtenons un nouveau masque contenant simplement l'intersection des deux images.
Je vous propose un exemple pour illustrer ceci, utilisant des matrices. Pour cela nous utiliserons le produit d'Hadamard ou produit composante par composante. N'ayez pas peur, cela n'est pas si compliqué que ça en a l'air.
Voyez plutôt :
$\begin{pmatrix} 1 & 1 & 0 & 0\\ 1 & 1 & 0 & 0\\ 1 & 1 & 0 & 0\\ 1 & 1 & 0 & 0 \end{pmatrix} . \begin{pmatrix} 1 & 1 & 1 & 1\\ 1 & 1 & 1 & 1\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 1 & 0 & 0\\ 1 & 1 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{pmatrix}$
Grâce à ce calcul, toute valeur non-nulle correspond donc à un pixel étant en collision entre les deux objets. Il pourrait même être envisageable d'utiliser un seuil pour les valeurs intermédiaires entre 0 et 1, pour considérer s'il y a collision ou non.
Dans l'encadré rouge de la figure suivante, je vous laisse apprécier ce que cette méthode pourrait donner localement pour notre problème de collision entre les objets voiture et mur.
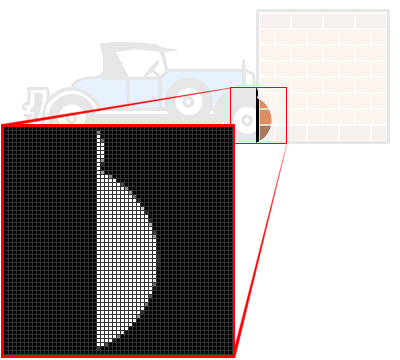
Une fois cette multiplication faite, nous n'allons plus qu'à parcourir l'ensemble des pixels pour détecter si les pixels dépassent le seuil d'opacité définit (ou son carré si vous souhaitez prendre en compte la multiplication appliquée aux valeurs de base). Un seul pixel dépassant le seuil d'opacité est alors synonyme de collision.
Application en code
Une méthode prête à l'emploi
Vous ayant déjà détaillé le principe, je vais simplement ici vous exposer le code d'une classe intégrant une méthode statique réalisant ce travail à partir d'objets d'affichage quelconques.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 | package { import flash.display.DisplayObject; import flash.display.BitmapData; import flash.geom.Matrix; import flash.geom.Point; import flash.geom.Rectangle; public class Collision { public function Collision() { throw new Error('Classe abstraite'); } static public function tester(obj1:DisplayObject, obj2:DisplayObject, seuil:uint):Boolean { var collision:Boolean = false; if (obj1.hitTestObject(obj2) == true) { var img1:BitmapData = creerBitmapData(obj1); var img2:BitmapData = creerBitmapData(obj2); var rect1:Rectangle = obj1.getBounds(obj1); var rect2:Rectangle = obj2.getBounds(obj2); var pos1:Point = new Point(obj1.x + rect1.x, obj1.y + rect1.y); var pos2:Point = new Point(obj2.x + rect2.x, obj2.y + rect2.y); collision = img1.hitTest(pos1, seuil, img2, pos2, seuil); } return collision; } static private function creerBitmapData(objet:DisplayObject):BitmapData { var image:BitmapData = new BitmapData(objet.width, objet.height, true, 0x00000000); var rect:Rectangle = objet.getBounds(objet); var transformation:Matrix = new Matrix(); transformation.translate(-rect.x, -rect.y); image.draw(objet, transformation); return image; } } } |
Comme je l'ai dit avant, tout repose sur la méthode hitTest() de la classe BitmapData. Le reste est uniquement la mise en place des éléments à transmettre à cette méthode.
La méthode proposée ci-dessus possède néanmoins un petit défaut. En effet, les diverses transformations appliquées à l'objet ne sont pas prises en compte, et généreront des bugs. Les objets d'affichage utilisés doivent ne doivent donc subir aucune transformation. Néanmoins, ceci peut être corrigé en les prenant en compte lors du tracé des BitmapData.
Un exemple d'utilisation
Pour tous ceux qui souhaiterez voir l'efficacité de la méthode statique donnée précédemment, je vous propose ci-dessous un petit code d'exemple. Regardez alors la simplicité d'utilisation de cette méthode. Encore une fois, un grand merci à la POO.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | var obj1:Shape = new Shape(); obj1.graphics.lineStyle(20, 0x000000); obj1.graphics.drawCircle(200, 200, 100); var obj2:Shape = new Shape(); obj2.graphics.beginFill(0x880088); obj2.graphics.drawCircle(0, 0, 15); obj2 addChild(obj1); addChild(obj2); addEventListener(Event.ENTER_FRAME, maFonction); function maFonction():void { obj2.x = mouseX; obj2.y = mouseY; if (Collision.tester(obj1, obj2, 0x11)) { obj1.filters = new Array(new GlowFilter()); }else{ obj1.filters = new Array(); } } |
Ce chapitre n'était qu'une introduction à la théorie des collisions. Même si vous savez désormais répondre à la plupart de vos besoins en termes de collisions, n'hésitez pas à vous perfectionner, notamment grâce au tutoriel « Théorie des collisions » de Fvirtman.
En résumé
- La détection d'une collision entre deux objets d'affichage se fait à l'aide d'une fonction booléenne.
- Suivants la forme des objets d'affichage et la précision de détection souhaitée, ces fonctions de tests de collisions doivent être différentes.
- Pour tout
DisplayObject, la méthodehitTestObject()permet de détecter des collisions entre deux objets à partir de leur cadre de sélection. - La méthode
hitTestPoint()de la classeDisplayObjectsert à tester une éventuelle collision entre un objet quelconque et un point. - Pour affiner au mieux les collisions entre deux objets aux formes complexes, la méthode
hitTest()de la classeBitmapDataeffectue des tests au niveau des pixels. - Les effets engendrées par une collision doivent être traités en dehors des fonctions booléennes de détection des collisions.