La méthode de Simpson

Comme nous l’avons vu dans le chapitre précédent, la méthode des trapèzes est plus précise que la méthode des rectangles. Notre but dans ce chapitre est de trouver une manière de se rapprocher encore plus de la courbe.

Principe de la méthode

La méthode de Simpson consiste à remplacer la fonction ff sur chaque intervalle par une fonction qui sera un trinôme. En effet, nous allons l’approcher par un polynôme de degré 2 qui passe pas les points Mk(xk,f(xk))M_k(x_k, f(x_k)), Mk+1(xk+1,f(xk+1))M_{k + 1}(x_{k + 1}, f(x_{k + 1})) et par le point au milieu Mk,5(xk,5,f(xk,5))M_{k{,}5}(x_{k{,}5}, f(x_{k{,}5})) avec xk,5=xk+xk+12x_{k{,}5} = \frac{x_k + x_{k + 1}}{2}.

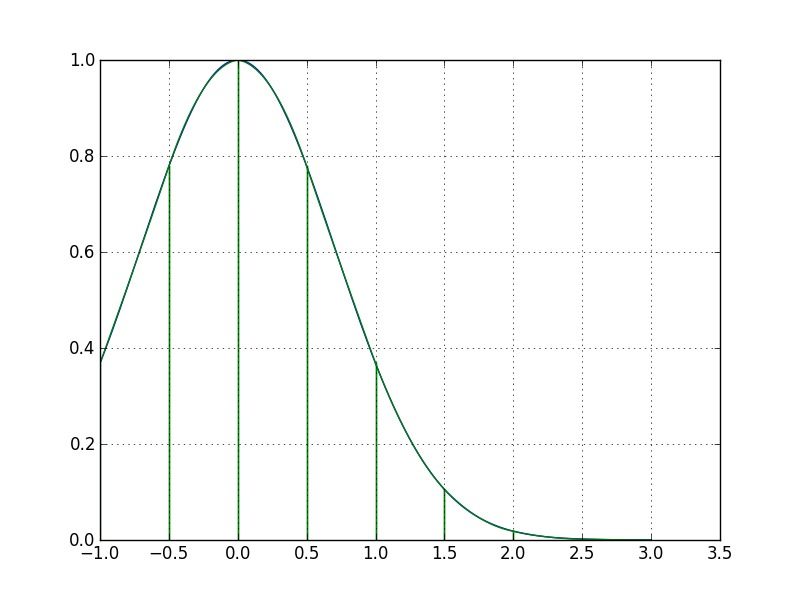
Les trinômes, ça marche.
Les trinômes, ça marche.

La courbe de la fonction ff est quasiment confondue avec les courbes des fonctions gkg_k.

Cependant, nous ne savons toujours pas que sont nos polynômes. En fait, il existe un unique polynôme de degré 2 qui vérifie les conditions que nous lui imposons. Pour le construire nous allons utiliser les polynômes interpolateurs de Lagrange. Si vous ne les connaissez pas, ça ne fait rien, nous allons construire notre polynôme pas par pas.

Récapitulons ce que nous demandons au polynôme QkQ_k.

  • L’image de xkx_k par la fonction polynomiale associée doit être f(xk)f(x_k).
  • L’image de xk,5x_{k{,}5} par la fonction polynomiale associée doit être f(xk,5)f(x_{k{,}5}).
  • L’image de xk+1x_{k + 1} par la fonction polynomiale associée doit être f(xk+1)f(x_{k + 1}).

Les autres points ne nous importent donc pas.

Pour construire ce polynôme, nous allons construire trois polynômes :

  • LkL_{k} tel que Lk(xk)=1L_{k}(x_k) = 1, Lk(xk,5)=0L_{k}(x_{k{,}5}) = 0 et Lk(xk+1)=0L_{k}(x_{k + 1}) = 0.
  • Lk,5L_{k{,}5} tel que Lk,5(xk)=0L_{k{,}5}(x_k) = 0, Lk,5(xk,5)=1L_{k{,}5}(x_{k{,}5}) = 1 et Lk,5(xk+1)=0L_{k{,}5}(x_{k + 1}) = 0.
  • Lk+1L_{k + 1} tel que Lk+1(xk)=0L_{k + 1}(x_k) = 0, Lk+1(xk,5)=0L_{k + 1}(x_{k{,}5}) = 0 et Lk+1(xk+1)=1L_{k + 1}(x_{k + 1}) = 1.

On les construit de cette manière :

Lk=(X−xk+1)(X−xk,5)(xk−xk+1)(xk−xk,5).Lk,5=(X−xk+1)(X−xk)(xk,5−xk+1)(xk,5−xk).Lk+1=(X−xk)(X−xk,5)(xk+1−xk)(xk+1−xk,5).\begin{aligned} L_{k} &= \frac{(X - x_{k + 1})(X - x_{k{,}5})} {(x_k - x_{k + 1}) (x_k - x_{k{,}5})}.\\ L_{k{,}5} &= \frac{(X - x_{k + 1})(X - x_k)} {(x_{k{,}5} - x_{k + 1}) (x_{k{,}5} - x_k)}.\\ L_{k + 1} &= \frac{(X - x_k)(X - x_{k{,}5})} {(x_{k + 1} - x_k) (x_{k + 1} - x_{k{,}5})}. \end{aligned}

Nous pouvons vérifier, ces polynômes font bien ce qu’on leur demande. Par exemple :

Lk(xk)=(xk−xk+1)(xk−xk,5)(xk−xk+1)(xk−xk,5)=1.Lk(xk+1)=(xk+1−xk+1)(xk+1−xk,5)(xk−xk+1)(xk−xk,5)=0.Lk(xk,5)=(xk,5−xk+1)(xk,5−xk,5)(xk−xk+1)(xk−xk,5)=0.\begin{aligned} L_{k}(x_k) &= \frac{(x_k - x_{k + 1})(x_k - x_{k{,}5})} {(x_k - x_{k + 1}) (x_k - x_{k{,}5})} = 1.\\ L_{k}(x_{k + 1}) &= \frac{(x_{k + 1} - x_{k + 1})(x_{k + 1} - x_{k{,}5})} {(x_k - x_{k + 1}) (x_k - x_{k{,}5})} = 0.\\ L_{k}(x_{k{,}5}) &= \frac{(x_{k{,}5} - x_{k + 1})(x_{k{,}5} - x_{k{,}5})} {(x_k - x_{k + 1}) (x_k - x_{k{,}5})} = 0. \end{aligned}

Maintenant, il est très simple de construire QkQ_k :

Qk=f(xk)Lk+f(xk,5)Lk,5+f(xk+1)Lk+1. Q_k = f(x_k) L_k + f(x_{k{,}5}) L_{k{,}5} + f(x_{k + 1}) L_{k + 1}.

On obtient bien un polynôme qui satisfait aux contraintes que nous lui avions imposées.

Calcul de l’intégrale

Il nous reste maintenant le plus gros du travail à faire. Il nous faut calculer l’intégrale de QkQ_k. Et pour cela, il nous faut calculer les intégrales de LkL_k, de Lk,5L_{k{,}5} et de Lk+1L_{k + 1}.

Pour faciliter l’écriture, nous allons poser pour le calcul de ces intégrales i,5=mi{,}5 = m.

On a :

∫xkxk+1Lk(t)dt=∫xkxk+1(t−xk+1)(t−xm)(xk−xk+1)(xk−xm)dt. \int_{x_k}^{x_{k + 1}} L_k(t) \mathrm{d}t = \int_{x_k}^{x_{k + 1}} \frac{(t - x_{k + 1})(t - x_m)} {(x_k - x_{k + 1}) (x_k - x_m)} \mathrm{d}t.

Nous pouvons sortir la constante :

∫xkxk+1Lk(t)dt=1(xk−xk+1)(xk−xm)∫xkxk+1(t−xk+1)(t−xm)dt. \int_{x_k}^{x_{k + 1}} L_k(t) \mathrm{d}t= \frac{1}{{(x_k - x_{k + 1}) (x_k - x_m)}} \int_{x_k}^{x_{k + 1}} (t - x_{k + 1})(t - x_m) \mathrm{d}t.

En faisant une intégration par partie :

∫xkxk+1Lk(t)dt=1(xk−xk+1)(xk−xm)([(t−xm)(t−xk+1)22]xkxk+1−∫xkxk+1(t−xk+1)22dt). \int_{x_k}^{x_{k + 1}} L_k(t) \mathrm{d}t = \frac{1}{(x_k - x_{k + 1}) (x_k - x_m)} \left( \left[ (t - x_m)\frac{(t - x_{k + 1})^2}{2}\right]_{x_k}^{x_{k + 1}} - \int_{x_k}^{x_{k + 1}} \frac{(t - x_{k + 1})^2}{2} \mathrm{d}t \right).

Et là nous savons faire l’intégration et donc :

∫xkxk+1Lk(t)dt=−(xk−xk+1)2(xk−xm)2(xk−xk+1)(xk−xm)−12(xk−xk+1)(xk−xm)×[(t−xk+1)33]xkxk+1.\int_{x_k}^{x_{k + 1}} L_k(t) \mathrm{d}t = \frac{ - (x_k - x_{k + 1})^2 (x_k - x_m) } { 2 (x_k - x_{k + 1}) (x_k - x_m) } - \frac{1}{2 (x_k - x_{k + 1} ) (x_k - x_m)} \times \left[ \frac{ (t - x_{k + 1})^3} {3}\right]_{x_k}^{x_{k + 1}}.

Nous poursuivons le calcul pour obtenir :

∫xkxk+1Lk(t)dt=(xk+1−xk)2+(xk−xk+1)26(xk−xm).\int_{x_k}^{x_{k + 1}} L_k(t) \mathrm{d}t = \frac{ (x_{k + 1} - x_k)}{2} + \frac{ (x_k - x_{k + 1} )^2}{6 (x_k - x_m )}.

Et finalement, sachant que xk+1−xk=δx_{k + 1} - x_k = \delta et que xk−xm=−xk+1−xk2=−δ2x_k - x_m = -\frac{x_{k + 1} - x_k}{2} = -\frac{\delta}{2}, on a :

∫xkxk+1Lk(t)dt=(12−13)×δ=δ6. \int_{x_k}^{x_{k + 1}} L_k(t) \mathrm{d}t = \left( \frac{1}{2} - \frac{1}{3}\right) \times \delta = \frac{\delta}{6}.

Le même calcul mène à

∫xkxk+1Lk+1(t)dt=δ6. \int_{x_k}^{x_{k + 1}} L_{k + 1}(t) \mathrm{d}t = \frac{\delta}{6}.

De la même manière, nous calculons l’intégrale de LmL_m :

∫xkxk+1Lm(t)dt=∫xkxk+1(t−xk+1)(t−xk)(xm−xk+1)(xm−xk)dt. \int_{x_k}^{x_{k + 1}} L_m(t) \mathrm{d}t = \int_{x_k}^{x_{k + 1}} \frac{(t - x_{k + 1})(t - x_k)} {(x_m - x_{k + 1}) (x_m - x_k)} \mathrm{d}t.

Toujours en sortant la constante :

∫xkxk+1Lm(t)dt=1(xm−xk+1)(xm−xk)∫xkxk+1(t−xk+1)(t−xk)dt. \int_{x_k}^{x_{k + 1}} L_m(t) \mathrm{d}t = \frac{1}{(x_m - x_{k + 1}) (x_m - x_k)} \int_{x_k}^{x_{k + 1}} (t - x_{k + 1})(t - x_k) \mathrm{d}t.

Et là, on fait la même intégration par partie que précédemment :

∫xkxk+1Lm(t)dt=1(xm−xk+1)(xm−xk)([(t−xk)(t−xk+1)22]xkxk+1−∫xkxk+1(t−xk+1)22dt). \int_{x_k}^{x_{k + 1}} L_m(t) \mathrm{d}t = \frac{1}{(x_m - x_{k + 1}) (x_m - x_k)} \left( \left[ (t - x_k)\frac{(t - x_{k + 1})^2}{2} \right]_{x_k}^{x_{k + 1}} - \int_{x_k}^{x_{k + 1}} \frac{(t - x_{k + 1})^2}{2} \mathrm{d}t \right).

D’où :

∫xkxk+1Lm(t)dt=12(xm−xk+1)(xm−xk)×[(t−xk+1)33]xkxk+1.\int_{x_k}^{x_{k + 1}} L_m(t) \mathrm{d}t = \frac{1}{2(x_m - x_{k + 1}) (x_m - x_k)} \times \left[ \frac{ (t - x_{k + 1})^3} {3}\right]_{x_k}^{x_{k + 1}}.

Nous poursuivons le calcul pour obtenir :

∫xkxk+1Lm(t)dt=12(xm−xk+1)(xm−xk)×−(xk−xk+1)33.\int_{x_k}^{x_{k + 1}} L_m(t) \mathrm{d}t = \frac{1}{2(x_m - x_{k + 1}) (x_m - x_k)} \times \frac{ -(x_k - x_{k + 1})^3}{3}.

Et finalement, sachant que xk+1−xk=δx_{k + 1} - x_k = \delta, que xm−xk=xk+1−xk2=δ2x_m - x_k = \frac{x_{k + 1} - x_k}{2} = \frac{\delta}{2} et que xm−xk+1=−xk+1−xk2=−δ2x_m - x_{k + 1} = -\frac{x_{k + 1} - x_k}{2} = -\frac{\delta}{2}, on a :

∫xkxk+1Lm(t)dt=−42δ2×−δ33=2δ3. \int_{x_k}^{x_{k + 1}} L_m(t) \mathrm{d}t = - \frac{4}{2 \delta^2} \times \frac{- \delta^3}{3} = \frac{2\delta}{3}.

Grâce à ces deux calculs, nous pouvons calculer l’intégrale de QkQ_k :

∫xkxk+1Qk(t)dt=∫xkxk+1f(xk)Lk(t)dt+f(xm)Lm(t)dt+f(xk+1)Lk+1(t)dt=f(xk)∫xkxk+1Lk(t)dt+f(xm)∫xkxk+1Lm(t)dt+f(xk+1)∫xkxk+1Lk+1(t)dt=δf(xk)6+2δf(xm)3+δf(xk+1)6=δ3(f(xk)+f(xk+1)2+2f(xm)). \begin{aligned} \int_{x_k}^{x_{k + 1}} Q_k(t) \mathrm{d}t &= \int_{x_k}^{x_{k + 1}} f(x_k) L_k(t) \mathrm{d}t + f(x_m) L_m(t) \mathrm{d}t + f(x_{k + 1}) L_{k + 1}(t) \mathrm{d}t\\ &= f(x_k) \int_{x_k}^{x_{k + 1}} L_k(t) \mathrm{d}t + f(x_m) \int_{x_k}^{x_{k + 1}}L_m(t) \mathrm{d}t + f(x_{k + 1}) \int_{x_k}^{x_{k + 1}}L_{k + 1}(t) \mathrm{d}t\\ &= \frac{ \delta f(x_k)}{6} + \frac{2 \delta f(x_m)}{3} + \frac{\delta f(x_{k + 1})}{6}\\ &= \frac{\delta}{3} \left(\frac{f(x_k) + f(x_{k + 1})}{2} + 2f(x_m) \right). \end{aligned}

Ouf, c’était un travail de longue haleine, mais le plus dur est maintenant fait.

Calcul de l’intégrale complète

Il ne nous reste plus qu’à calculer la somme des intégrales de QkQ_k pour enfin avoir l’approximation de notre intégrale (on revient à notre « i,5i{,}5 ») :

I(f)≈∑k=0n−1∫xkxk+1Qk(t)dt=∑k=0n−1δ3(f(xk)+f(xk+1)2+2f(xk,5)). I(f) \approx \sum_{k = 0}^{n - 1} \int_{x_k}^{x_{k + 1}} Q_k(t) \mathrm{d}t = \sum_{k = 0}^{n - 1} \frac{\delta}{3} \left(\frac{f(x_k) + f(x_{k + 1})}{2} + 2f(x_{k{,}5}) \right).

Comme d’habitude on sort la constante de la somme :

I(f)≈δ3∑k=0n−1(f(xk)+f(xk+1)2+2f(xk,5)). I(f) \approx \frac{\delta}{3} \sum_{k = 0}^{n - 1} \left(\frac{f(x_k) + f(x_{k + 1})}{2} + 2f(x_{k{,}5}) \right).

On remarque que tous les xkx_k sont comptés deux fois sauf le premier (x0x_0) et le dernier (xnx_n). Donc on peut les sortir de la somme (mais ça nous oblige à sortir le f(x0,5)f(x_{0{,}5}) de la somme) :

I(f)≈δ3(f(x0)+f(xn)2+2f(x0,5)+∑k=1n−1(f(xk)+2f(xk,5))). \boxed{I(f) \approx \frac{\delta}{3} \left( \frac{f(x_0) + f(x_n)}{2} + 2f(x_{0{,}5}) +\sum_{k = 1}^{n - 1} \left(f(x_k) + 2f(x_{k{,}5}) \right) \right)}.

Et c’est cette écriture que nous allons garder.

Algorithme et tests

Écrivons cet algorithme en Python (pour obtenir les ,5{,}5, il nous suffit d’ajouter δ2\frac{\delta}{2}) :

def simpson(f, a, b, n):
    pas = (b - a) / n
    somme = (f(a) + f(b)) / 2 + 2 * f(a + pas / 2)  # On initialise la somme
    x = a + pas           # La somme commence à x_1 
    for i in range(1, n): # On calcule la somme 
        somme += f(x) + 2 * f(x + pas / 2)
        x += pas
    return somme * pas / 3   # On retourne cette somme fois le pas / 3

Comme pour la méthode des rectangles et celle des trapèzes, essayons-la avec la fonction cosinus sur [0,π][0, \pi], en découpant l’intervalle en 100. On obtient alors ce graphe.

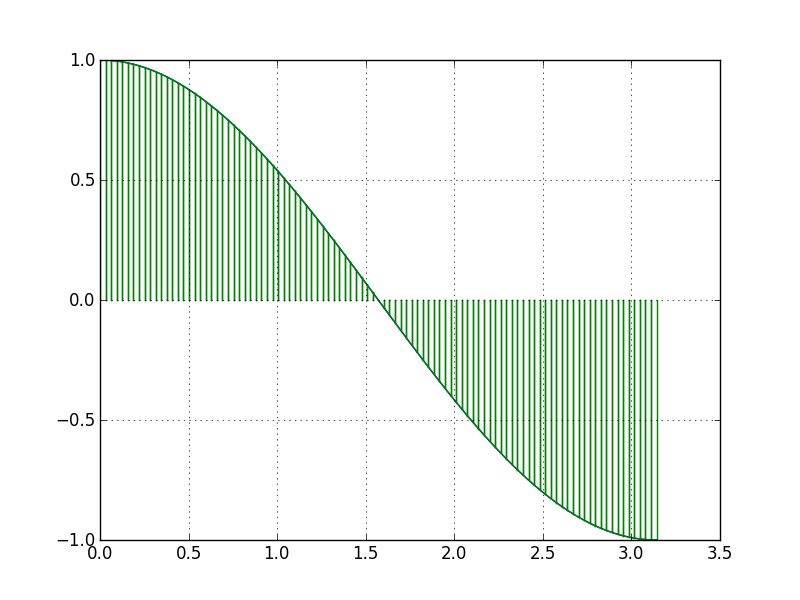
La méthode de Simpson sur la fonction cosinus.
La méthode de Simpson sur la fonction cosinus.

Le graphe nous permet déjà de savoir que le résultat obtenu sera proche de la vraie valeur de l’intégrale, et en effet, nous obtenons un résultat de l’ordre de 10-15. Ce résultat est bien proche de 0.

En fait, la méthode de Simpson est moins précise que la méthode des trapèzes dans le cas particulier de la fonction cosinus. Dans le bloc secret qui suit, nous verrons pourquoi. Il ne s’agit que d’un cas particulier, mais généralement, sur une fonction suffisamment régulière (voir le chapitre suivant), la méthode de Simpson est plus précise.

En fait, la méthode des trapèzes est censé donner un résultat nul pour la fonction cosinus sur [0,π][0, \pi]. En effet, appliquer la méthode des trapèzes avec un pas nn dans ce cas consiste à calculer

πn(cos⁡(0)+cos⁡(π)2+∑k=1n−1cos⁡(kπn)).\frac{\pi}{n} \left( \frac{\cos(0) + \cos(\pi)}{2} + \sum_{k = 1}^{n - 1} \cos\left( \frac{k\pi}{n}\right) \right).

On a cos⁡(0)+cos⁡(π)=0\cos(0) + \cos(\pi) = 0, il nous reste à calculer la somme (appelons la SnS_n). On a en faisant le changement d’indice l=n−kl = n - k,

Sn=∑l=1n−1cos⁡((l−n)πn)=∑l=1n−1cos⁡(lπn−π)=∑l=1n−1cos⁡(−lπn)=∑l=1n−1−cos⁡(lπn)=−Sn.\begin{aligned} S_n &= \sum_{l = 1}^{n - 1} \cos\left( \frac{(l - n)\pi}{n} \right)\\ &= \sum_{l = 1}^{n - 1} \cos\left(\frac{l\pi}{n} - \pi \right)\\ &= \sum_{l = 1}^{n - 1} \cos\left(-\frac{l\pi}{n} \right)\\ &= \sum_{l = 1}^{n - 1} -\cos\left(\frac{l\pi}{n} \right)\\ &= -S_n. \end{aligned}

On en déduit que SnS_n est nul, et donc on obtient bien que la méthode des trapèzes donne un résultat nul dans ce cas particulier (l’ordinateur ne nous donne pas 0 à cause des erreurs d’approximations).

Un autre fait que nous pouvions remarquer est que (toujours pour la fonction cosinus entre 00 et π\pi), la méthode des rectangles nous donne πn\frac{\pi}{n}, car elle consiste à calculer

πn(∑k=0n−1cos⁡(kπn))=πn(cos⁡(0)+Sn)=πn.\begin{aligned} \frac{\pi}{n} \left(\sum_{k = 0}^{n - 1} \cos\left( \frac{k\pi}{n}\right) \right) &= \frac{\pi}{n} \left( \cos(0) + S_n \right)\\ &= \frac{\pi}{n}. \end{aligned}

Il est maintenant temps de voir ce que cette méthode nous donne sur notre exemple.

print(simpson(f, 0, 1, 100))

Avec elle on obtient environ 0,746824.