Dans la partie précédente, nous avons vu les formules du sinus, cosinus et tangente pour un angle aigu positif. Dans cette partie, l’objectif est de généraliser cela à tous les angles, autrement dit aux angles obtus ainsi qu’aux angles orientés négativement.
- Configurations en termes de cadran
- Formules généralisées pour cosinus, sinus et tangente
- Cercle trigonométrique
- Valeurs remarquables et transformations
Configurations en termes de cadran
Pour commencer, il est important de passer un peu de temps à observer l’agencement des points intéressants, tel que le projeté d’un point sur l’autre côté, selon l’ouverture de l’angle. Ces observations nous seront utiles dans la section suivante, quand nous ferons la généralisation des formules vues dans la partie précédente.
Nous observerons la position relative d’un point sur un côté et de son projeté par rapport au sommet de l’angle et aux côtés. C’est une petiet gymnastique que vous aurez à faire en pratique, parce que rien ne dit que votre figure sera bien rangée avec le premier côté de l’angle horizontal sur votre feuille.
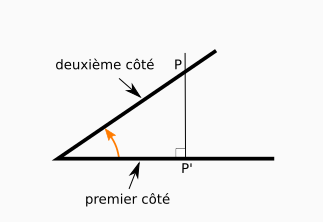
Angles positifs entre 0° et 90°
Il s’agit de la situation vue précédemment. Si on place le côté de l’angle horizontalement et qu’on fait pointer le premier côté vers la droite, le sommet étant à gauche, on peut faire les observations suivantes :
- le deuxième côté est au-dessus de la droite définie par le premier côté ;
- le projeté d’un point pris sur le deuxième côté se situe sur le premier côté, à droite du sommet.
Prenez bien conscience que ces placements sont relatifs. Il faut bien positionner le premier côté.
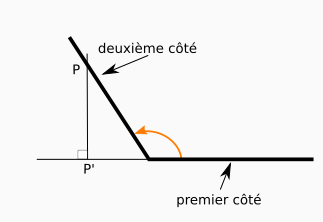
Angles positifs entre 90° et 180° ou négatifs entre -180° et -270°
Considérons un angle orienté positivement compris entre 90° et 180°. Comme dans le paragraphe précédent, nous nous intéressons à la position du côté et du projeté.
Le projeté orthogonal tombe en dehors du premier côté. Mais ce n’est pas un problème ! Le projeté orthogonal est une notion qui concerne des droites, pas des segments, il suffit de prolonger le côté pour effectuer la projection.
On observe alors les choses suivantes :
- le deuxième côté est au-dessus de la droite définie par le premier côté ;
- le projeté d’un point pris sur le deuxième côté se situe à gauche du sommet, sur le coté une fois prolongé.
Il s’agit de la même configuration pour un angle négatif compris entre -180° et -270°.
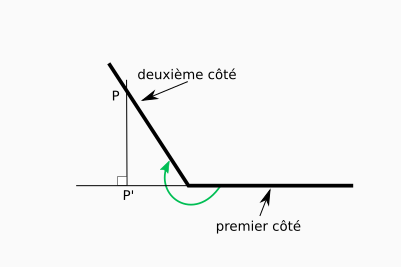
Angles positifs entre 180° et 270° ou négatifs entre -90° et -180°
Considérons maintenant un angle dont la mesure est supérieure à 180° mais inférieure à 270°. Le projeté orthogonal est encore une fois en dehors du côté.
On observe les positions relatives suivantes :
- le deuxième côté est en dessous de la droite définie par le premier côté ;
- le projeté d’un point pris sur le deuxième côté se situe à gauche du sommet, sur le coté une fois prolongé.
Il s’agit de la même configuration pour un angle négatif compris entre -90° et -180°. Je vous laisse imaginer la figure.
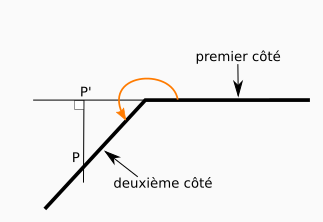
Angles positifs entre 270° et 360° ou négatifs entre 0° et -90°
Maintenant, pour un angle positif entre 270° et 360°, on observe les positions relatives suivantes :
- le deuxième côté est en dessous de la droite définie par le premier côté ;
- le projeté d’un point pris sur le deuxième côté se situe à droite du sommet, sur le coté une fois prolongé.
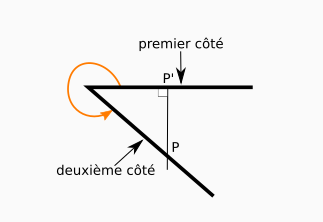
Il s’agit de la même configuration pour un angle négatif comris entre 0° et -90°.
Synthèse des configurations
On a finalement quatre configurations selon où se trouve le projeté et le point par rapport au sommet.
- projeté orthogonal à droite du sommet et point P au-dessus du sommet ;
- projeté orthogonal à gauche du sommet et point P au-dessus du sommet ;
- projeté orthogonal à gauche du sommet et point P au-dessous du sommet ;
- projeté orthogonal à droite du sommet et point P au-dessous du sommet ;
Ces configurations correspondent à des quartiers, appelés cadrans, numérotés de 1 à 4 dans le sens positif, comme le montre le schéma ci-dessous :
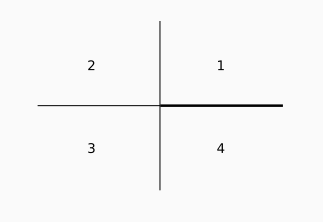
Il est assez facile de déterminer un cadran, tant qu’on se positionne bien par rapport au premier côté de l’angle, c’est-à-dire celui dont la petite flèche définissant l’angle part.
Formules généralisées pour cosinus, sinus et tangente
Motivations
On souhaite pouvoir distinguer les différentes configurations et donc distinguer des angles qui auraient autrement les mêmes cosinus, sinus et tangente.
La manière de faire ça est d’ajouter un signe aux distances géométriques. Autrement dit, nous utiliserons ce qu’on appelle des distances algébriques.
Pour la distance entre le sommet et le projeté :
- si le projeté est à droite du sommet, la distance algébrique est positive ;
- si le projeté est à gauche du sommet, la distance algébrique est négative.
On note cette distance algébrique .
Similairement, pour la distance entre le point et son projeté :
- si le point est au-dessus du côté, la distance algébrique est positive ;
- si le point est en dessous du côté, la distance algébrique est négative.
La distance entre le sommet et le point, c’est-à-dire ce qui correspond à l’hypoténuse, reste une distance normale, toujours positive.
Formules généralisées
On peut généraliser les formules en utilisant des distances algébriques au lieu des simples longueurs comme dans la partie précédente.
L’ordre des lettres a une importance !
On peut retenir relativement facilement :
- si la distance met en jeu le sommet, alors il est en premier ;
- sinon, s’il s’agit d’un point et de son projeté, alors le projeté est en premier.
Regarder les orientations des distances algébriques est un peu laborieux, même si cela fonctionne parfaitement à tous les coups et permet de ne retenir qu’une seule formule. Une manière un peu plus imagée de retenir les signes est de regarder la configuration dans laquelle on se trouve :
- pour le cosinus,
- les angles du 1er et 4e cadran auront un cosinus positif ;
- les angles du 2e et 3e cadran auront un cosinus négatif ;
- pour le sinus,
- les angles du 1er et 2e cadran auront un sinus positif ;
- les angles du 3e et 4e cadran auront un sinus négatif ;
- pour la tangente,
- les angles du 1er et 3e cadran auront une tangente positive ;
- les angles du 2e et 4e cadran auront une tangente négative ;
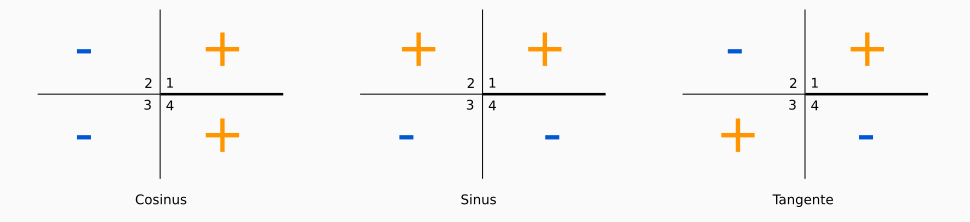
Tout ça est un peu compliqué, le cercle trigonométrique que nous aidera à bien retenir tout ça.
Cercle trigonométrique
Le cercle trigonométrique est un moyen mnémotechnique qui aide à retenir ou retrouver les signes, de nombreuses valeurs remarquables et les formules de transformation pour tous les angles. Il permet de faire tout ce que le triangle rectangle trigonométrique offre, et plus encore.
Construction du cercle trigonométrique
On se place dans un repère d’origine , et on y trace un cercle de rayon . La droite est tangente au cercle.
Le point H est le projeté du point . Ainsi, l’abscisse de correspond à . L’ordonnée du point vaut .
Quand on prolonge le rayon , on atteint un point sur la droite tangente. L’ordonnée du point est . C’est de là que vient d’ailleurs le nom de tangente.
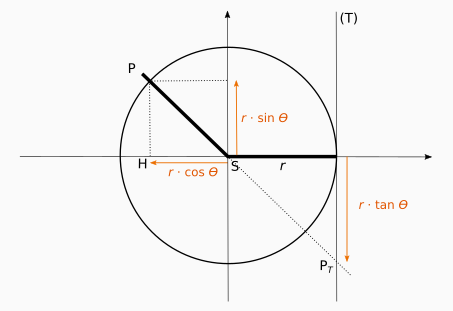
Attribuer les bons signes selon l’angle
Dans la figure précédente, il est facile de retrouver les signes dans le repère : il suffit de regarder le signe de l’abscisse et l’ordonnée pour retrouver celui du sinus et du cosinus. De même pour la tangente, le signe sera négatif en dessous de l’axe des abscisses et positif au dessus.
Valeurs remarquables et transformations
Valeurs remarquables
Le tableau suivant donne quelques valeurs remarquables qu’il est utile de retenir.
Vous constaterez qu’il n’y a que quelques angles aigus positifs, car il est possible de trouver les autres valeurs grâce aux formules de transformation !
Si vous souhaitez démontrer ces valeurs, il est possible de le faire avec des outils de géométrie plus simples, tels que le théorème de Pythagore, notamment.
Transformations
Angles opposés
Il est possible d’obtenir les valeurs des cosinus, sinus et tangentes d’angles négatifs à partir de l’angle positif de même valeur.
Il est assez facile de se convaincre de leur justesse avec le cercle trigonométrique en observant attentivement.
Rotations et symétries
D’abord, commençons par les formules en . Cela correspond à faire une rotation de 180° ( rad). Vous pouvez visualiser ces résultats dans le cercle trigonométrique
Ensuite, voilà quelques formules en . Cela correspond à prendre le symétrique par rapport à l’axe des ordonnées dans le cercle trigonométrique.
Maintenant, les formules en . Cela correspond à une rotation d’un quart de tour.
Toutes se démontrent relativement facilement, notamment avec l’aide du cercle trigonométrique ! Il existe encore d’autres formules, mais celles-ci sont les plus utiles.