Dans cette partie, on s’intéresse au cas particulier d’un angle aigu positif, c’est-à-dire un angle qui fait 90° ou moins et est orienté positivement. Ce qui est développé dans cette partie sera généralisé à tous les angles dans la partie suivante.
- Projections orthogonales
- Relations de proportionnalités et cosinus, sinus, tangente
- Triangle rectangle trigonométrique
- Applications
Projections orthogonales
Pour comprendre les sections suivantes, il est utile de faire un détour pour introduire les notions de projection et projection orthogonale.
Si on prend un point sur un côté d’un angle, il est possible de le projeter sur l’autre côté. Projeter un point d’un côté sur l’autre, cela consiste à prendre une droite passant par ce point et intersectant l’autre côté en un point qu’on appelle alors le projeté du premier point.
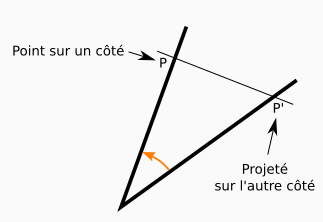
Dans notre cas, nous nous intéresserons à une projection particulière : celle où le projeté est le plus proche possible du point qu’on projette. On appelle cela une projection orthogonale, car la droite de projection forme alors un angle droit avec le côté sur lequel le point se retrouve projeté.
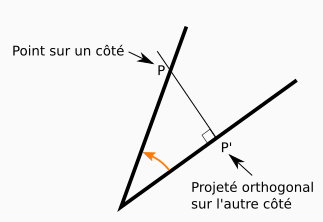
Soyez attentifs : dans une projection orthogonale, le projeté est le point où se trouve l’angle droit et pas l’inverse !
Relations de proportionnalités et cosinus, sinus, tangente
Proportionnalité de longueurs dans un angle
Quand on fait une projection orthogonale, on voit que la distance entre un point et son projeté dépend de l’ouverture de l’angle et de la position du point d’origine. Cette distance mesure l’écartement de l’angle à une certaine distance du sommet. Plus un angle est ouvert, plus l’écartement sera grand à une distance donnée du sommet.
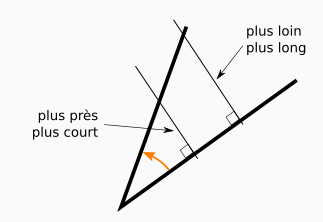
Plus précisément, pour un angle fixé, cet écart sera proportionnel à la distance au sommet. On a aussi d’autres relations de proportionnalité entre les différentes longueurs ainsi formées. C’est un cas particulier du théorème de Thalès.
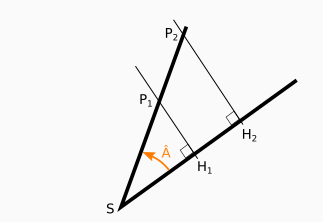
Ces relations de proportionnalité sont les suivantes :
Cosinus, sinus, tangente
Comme on parle tout le temps de ces relations de proportionnalité en trigonométrie, elles ont été nommées.
Pour un angle aigu positif, le rapport de la longueur sur la longueur est le cosinus de l’angle Â, noté .
Pour un angle aigu positif, le rapport de la longueur sur la longueur est le sinus de l’angle Â.
Pour un angle aigu positif, le rapport de la longueur sur le côté est la tangente de l’angle Â.
Ces rapports sont fixes pour un angle de mesure donnée, en vertu de la proportionnalité. Notamment :
- peu importe quels points et projetés orthogonaux correspondants on choisit, la valeur sera la même ;
- deux angles de même mesure auront les mêmes sinus, cosinus et tangentes.
Notez bien que les définitions ici sont applicables seulement pour un angle aigu orienté positivement, mais nous généraliserons ça dans la partie suivante.
Triangle rectangle trigonométrique
En faisant un projeté orthogonal, on forme un triangle avec un angle droit, autrement dit un triangle rectangle.
Ce triangle rectangle est pratique comme synthèse pour se souvenir des définitions. Dans le cas d’un angle aigu orienté positivement, on peut en effet définir le cosinus, sinus et la tangente en fonction des cotés d’un triangle rectangle.
Quand on se focalise sur un angle en particulier, les côtés du triangle rectangle ont alors des désignations particulières :
- l'hypoténuse est le côté en face de l’angle droit,
- le côté opposé est le côté en face de l’angle qui nous intéresse ;
- le côté adjacent est le côté de l’angle où l’on trouve l’angle droit.
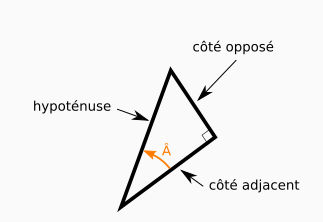
Les définitions sont alors les suivantes :
Souvent, on retient ces formules en retenant le mot CAHSOHTOA, qui sonne un peu comme « casse-toi ». On se remémore les formules avec les initiales, qui signifient : cosinus adjacent hypoténuse, sinus opposé hypoténuse, tangente opposé adjacent.
Retenez bien que le triangle rectangle est une manière de mieux retenir : le cosinus, sinus et tangente concernent les angles eux-mêmes, qu’un triangle rectangle ait été dessiné ou pas.
Applications
Calcul d’un cosinus, sinus et tangente à partir des distances
Calculons le cosinus, le sinus et la tangente de l’angle  de la figure ci-dessous. Les longueurs des côtés sont 3, 4 et 5 comme indiqués dans la figure ci-dessous.
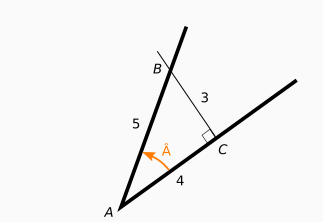
Avant de foncer tête baissée, il est utile de bien s’assurer de comprendre en profondeur et vérifier la cohérence, surtout si on débute.
Déjà, les longueurs indiquées prouvent bien que l’angle en C est bien droit. En effet, d’après le théorème de Pythagore, prouve que le triangle est rectangle en C. On en déduit que C est le projeté orthogonal de B sur l’autre côté de l’angle Â. L’angle  est aussi aigu et orienté positivement.
L’angle aigu positif et le triangle rectangle nous permettent d’appliquer les formules vues précédemment, avec la nomenclature suivante :
- l’hypoténuse du triangle ABC est , de longueur 5 ;
- le côté adjacent à Â est , de longueur 4 ;
- le côté opposé à Â est , de longueur 3.
Et donc d’après les formules de la section précédente :
Calcul d’une distance à partir d’une autre distance et d’un angle
Procédons maintenant avec trois exemples permettant de calculer une distance en connaissant une distance et l’angle. La figure sera à chaque fois la suivante et nous ajusteront les mesures des côtés.
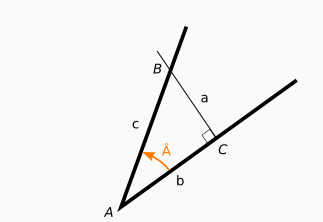
Exemple 1
Supposons qu’on veuille calculer BC en connaissant :
- la mesure de Â, ;
- la longueur de AB, 8.
Si on se place dans le triangle ABC rectangle en C et qu’on considère l’angle Â, AB joue le rôle de l’hypoténuse et BC le rôle du côté opposé. On peut alors utiliser le sinus, qui relie ces deux valeurs. On sait ainsi que :
En isolant BC et en remplaçant  par sa mesure, on en déduit que :
est une valeur remarquable et vaut (on en reparlera plus tard) ! Finalement :
Ce qui était la valeur recherchée.
Exemple 2
Supposons qu’on veuille calculer AB en connaissant :
- la mesure de Â, ;
- la longueur de AC, 23.
Si on se place dans le triangle ABC rectangle en C et qu’on considère l’angle Â, AB joue le rôle de l’hypoténuse et AC le rôle du côté adjacent. On peut ainsi utiliser le cosinus, qui relie ces deux valeurs :
Similairement à l’exemple 1, on peut isoler ce qui nous intéresse :
Autrement dit, en remplaçant par les valeurs numériques :
Il est possible de calculer la valeur exacte de , mais elle n’est pas particulièrement simple. Il est tout de même possible de calculer une approximation de , à l’aide de la calculatrice. Je trouve :
Exemple 3
Supposons qu’on veuille calculer AC en connaissant :
- la mesure de Â, ;
- la longueur de BC, 12.
Si on se place dans le triangle ABC rectangle en C et qu’on considère l’angle Â, BC joue le rôle du côté opposé et AC le rôle du côté adjacent. On peut ainsi utiliser la tangente, qui relie ces deux valeurs :
Le calcul est très similaire aux deux exemples précédents. se calcule de manière exacte, mais encore une fois, ce n’est pas particulièrement simple.
La valeur approchée qu’on trouve pour AC est :
Ce qu’il faut retenir de ces trois exemples, c’est qu’on peut jongler entre les distances connues pour retrouver les autres pour peu qu’on connaisse l’angle ! Il faut cependant toujours prendre soin de bien identifier l’angle droit et le rôle des différents côtés pour utiliser correctement les formules.
Utiliser sa calculatrice attentivement
Quand on utilise la calculatrice, il faut faire attention : par défaut, la calculatrice attend des angles en radians. C’est ce que nous avons fait dans les exemples précédents.
Mais imaginons que l’angle ait été donné en degré. Par exemple  mesure 30°. Alors il faut surtout ne pas faire calculer à la calculatrice n’importe quoi. Par exemple :
Ici, il s’agit du cosinus d’un angle de 30 radians (ce n’est pas un angle aigu, nous y reviendrons).
Ce que l’on veut calculer, c’est en fait :
Par défaut, les calculatrices vont calculer en radian et si vous avez un angle en degrés, il vous faudra le convertir auparavant. Certains outils ont des variantes qui acceptent les degrés (par exemple des fonctions , , ). D’autres outils encore, par exemple Wolfram Alpha vont essayer de deviner l’unité, et vous dire ce qu’ils ont choisi pour faire le calcul, pratique pour être sûr de son coup !
En bref : lisez le manuel de votre calculatrice ou outil favori et soyez attentifs !
Maintenant que nous avons vu les rapports trigonométriques dans le triangle, il est temps de passer à d’autres configuration d’angles qui ne forment pas des triangles de manière aussi évidente, tout en gardant les notions cohérentes.