Assurances, amortissement, TAEG...

Bon, il est temps de voir comment ça fonctionne concrètement, c’est-à-dire au niveau de ton portefeuille.

Nous l’avions dit, le crédit le plus courant est appelé crédit amortissable à taux fixe.

• à taux fixe : le taux ne varie pas sur toute la période du prêt. Sachez qu’il existe des prêts à taux variable, où le taux peut varier en fonction de variables macroéconomiques (taux directeurs de la Banque Centrale par exemple)
• amortissable : cela signifie qu’à chaque mensualité, on paye des intérêts, mais surtout on rembourse petit à petit le capital emprunté (en termes financiers, on l'amortit). A l’inverse, il existe par exemple des prêts in fine, où on ne paye que les intérêts pendant des années et on rembourse tout le capital la dernière année.

Il faut savoir que les intérêts ne sont calculés que sur le capital qui reste à rembourser, et non sur le capital emprunté total. Explications sur un prêt de 100 000€ à 2% sur 20 ans, qui entraîne une mensualité de 505,88€ (taux mensuel proportionnel : 0,16%) :

Cet algorithme est facile à implémenter sur un tableur type Excel. Si vous le faites, vous obtiendrez ce qu’on appelle un tableau d’amortissement, avec chaque mois les intérêts payés, le capital remboursé et le capital restant à rembourser, ce qu’on appelle le crédit restant dû ou CRD.

Il en ressort deux choses :

• Vous payez à chaque fois de moins en moins d’intérêts.
• Vous remboursez de plus en plus de capital (ce qu’on appelle aussi le principal).

Ce qui se traduit par le graphique ci-dessous. La hauteur des barres indique la mensualité payée. Elle est constante tout au long du remboursement, mais à l’intérieur, les intérêts sont décroissants et le capital remboursé (le principal) croissant.

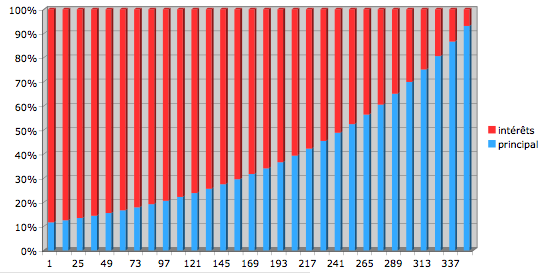
En quoi ces données sont importantes ?

• En cas de remboursement anticipé : si vous revendez votre bien avant la fin du crédit, il faut solder celui-ci et rembourser le Crédit Restant Dû (CRD) à la banque. Il n’est donc pas intéressant financièrement de revendre un bien immobilier très rapidement.
• S’il s’agit d’un investissement locatif, vous devez payer des impôts sur les loyers reçus. Or vous avez le droit de déduire de ces loyers les intérêts payés dans l’année (car ils constituent une charge financière), ce qui permet de payer moins d’impôts.

— Pour l’instant on n’a parlé que du taux du prêt. Mais il y a aussi les assurances.
— Exact. Un prêt immobilier est toujours assorti d’une assurance décès-invalidité. Cela permet, en cas de pépin grave, que l’assurance prenne à sa charge le remboursement du capital restant dû. Sur notre exemple, on avait un taux à 1,35 et une assurance à 0,23.
— Ce qui fait donc un taux réel de 1,58.
— Non, pas du tout.
— …?

L’assurance n’est pas calculée de manière identique. En fait elle est (généralement, sauf si indiqué différemment) calculée sur la totalité du montant emprunté, et non sur le capital restant dû.
Ainsi, sur 100 000€ empruntés, une assurance à 0,23% signifie que tu payeras 230€ par an (donc 19€ par mois) pendant 20 ans.
Tu ne peux donc pas ajouter ce taux au taux du prêt, vu que les calculs d’intérêts sont complètement différents. Par contre tu dois ajouter ces 19€ à tes mensualités.
— Du coup, il n’existe pas un indicateur, un taux équivalent, qui permettrait d’englober tout ça ?
— Si, cest le TAEG, on en parle juste après.

— Le TAE quoi ?
— TAEG : Taux Annuel Effectif Global.

Pour l’expliquer, prenons un exemple : tu empruntes 100 000€, à 2%. Tu calcules donc que tu auras une mensualité de 505€.
Mais pour t’accorder ton prêt, la banque va prendre des frais de dossier, disons 2000€, des frais de caution, disons 3000€, éventuellement des frais de courtage si tu es passé par un courtier, 1000€.
Tous ces 6000€ annexes, qui auront été nécessaires à l’obtention de ton prêt, elle va les intégrer au prêt. Tu empruntes donc au final 106 000€. Toujours à 2%, ce qui fait une mensualité de 536,24€.
— Ah oui, c’est plus la même chose…
— A cela tu rajoutes l’assurance. C’est 0,23%, mais de 106 000€ cette fois-ci. En effet, tu dois assurer tout le capital emprunté.
— On rajoute donc 20€ d’assurances. Ce qui fait 556€ de mensualités.
— OK, c’est le coût réel mensuel de ton prêt. Or toi tu voulais emprunter 100 000€ à la base.

Donc pour résumer, tu veux emprunter 100 000€, et tu te retrouves à payer une mensualité de 556€ sur 20 ans. En sortant ta calculatrice financière, tu trouves que ça correspond à un taux équivalent de : $3,03$%.

C’est ton TAEG. Le taux qui intègre tous les frais qui auront été nécessaires à ton emprunt. Ce taux est obligatoirement donné sur toutes les offres de prêt. Comme son calcul est le même pour toutes les banques (il est inscrit dans la loi), il te permet de comparer les prêts entre eux.

— Mais dans ton exemple, il suffit de comparer les mensualités.
— Dans cet exemple simple, oui. Mais il peut exister des structures de prêt un peu plus compliquées. Par exemple des prêts avec différé de remboursement où tu peux ne payer qu’une partie de la mensualité au début, puis un peu plus après (par exemple si tu achètes sur plan un appartement neuf qui ne sera livré que dans un an), des prêts structurés où tu as une certaine mensualité au début, puis une plus faible dans la deuxième moitié de ton prêt, etc.
Cela devient difficile de comparer ces prêts, ce que le TAEG va permettre.

Son calcul se base sur la formule d’actualisation vue au début. Il va prendre tous tes flux financiers différents (tes mensualités) et les actualiser avec un certain taux, pour que la somme de tous ces flux actualisés soit égale au capital que tu voulais réellement emprunter. Ce taux qui permet d’égaliser le capital et la somme des flux actualisés, c’est le TAEG.
La formule utilisée pour le calculer est donc :

$\boxed{K_{désiré}=\frac{M_1}{1+\frac{TAEG}{12}}+\frac{M_2}{(1+\frac{TAEG}{12})^2}+\frac{M_3}{(1+\frac{TAEG}{12})^3}+...+\frac{M_n}{(1+\frac{TAEG}{12})^n}}$

Note : comme on actualise les mensualités, on doit les actualiser avec le taux mensuel proportionnel, qui est égal au TAEG sur 12

Voilà, ce petit tutoriel se termine ici. Il nous aura permis d’aborder un sujet ô combien présent dans la vie de beaucoup. Cela aura aussi été l’occasion d’aborder quelques notions mathématiques (logarithme, suite, exponentielle) et de les mettre en relation avec un sujet concret.
Nous avons aussi un peu effleuré les mathématiques financières, domaine extrêmement vaste mais passionnant…
En espérant que cela vous inspire.