Salut chers amis zesteux,
Comme vous le savez peut-être, j’aime bien la musique. J’aime bien aussi savoir comment la musique est faite, et quand on va chercher un peu dans les principes fondamentaux, on se doit de faire un peu de physique et de traitement de signal. Dans ce tutoriel, je propose de s’intéresser à la reconnaissance de notes en testant sur des exemples simples.
La reconnaissance de notes consiste à retrouver la partition d’un morceau à partir du signal audio. Comme vous pouvez le penser, c’est loin d’être facile, et la preuve est que c’est encore un domaine de recherche actif. Alors on va faire des choses plutôt basiques, mais qui auront l’avantage de passer en revue les principes fondamentaux : on va reconnaître les notes dans un seul accord.
Disclaimer
Le principe de ce tuto est de se baser sur un point de vue plus musical que physique, parce qu’il y a plein de tutos de traitement du signal, mais pas beaucoup qui suivent cette approche. Par conséquent, il y aura forcément un peu de lexique emprunté à la musique, mais pas grand chose de compliqué.
- Le premier traitement du signal
- Le lien entre fréquences et musique
- Détecter une note
- Supprimer la note du signal
- Récap de l'algo
- Le résultat
Le premier traitement du signal
L’extrait audio
On va tout d’abord ouvrir l’extrait à analyser. Il ne s’agit que d’un accord, mais on fait des choses simples, c’est déjà assez compliqué comme ça. 
On peut le jouer pour voir ce que ça donne. Les notes sont la, do, mi, sol.
Je vous met le lien soundcloud ici pour que vous puissiez le télécharger si vous voulez l’étudier de votre côté.
Visualisation de l’extrait
Et on peut afficher notre petit extrait pour voir sa tête (amplitude en fonction du temps).

On peut faire quelques remarques : l’amplitude est en moyenne décroissante, ce qui est normal vu que l’extrait est un accord tenu qui est en conséquence de moins en moins fort. On peut aussi dire que le signal oscille autour de la valeur moyenne qui est . C’est normal : un son, c’est avant tout une compression de l’air, qui oscille donc autour de la pression moyenne ambiante. C’est dit avec les mains mais l’idée est là.
Il est important de noter que le signal est discret. C’est normal parce que c’est un signal numérique, donc il est représenté sous la forme d’un tableau. Par conséquent, on travaille nécessairement avec une approximation du signal d’origine.
Mettre en forme le signal
Avant de commencer les choses sérieuses, on va mettre le signal un peu plus en forme, pour pouvoir travailler plus facilement dessus.
Réduire l’attaque
Une première chose à faire est de réduire l’impact de l’attaque. L’attaque de la note, c’est le début du signal. Pour un instrument, ça correspond au début de la note. Pour un piano, c’est le moment où le marteau frappe les cordes.
Il se trouve que l’attaque est l’élément qui contient le plus d’informations à propos de la note : il est beaucoup plus simple de distinguer l’instrument à l’oreille quand on dispose de l’attaque et non pas simplement du continu qui vient après l’attaque. Seulement, l’attaque est très difficile à traiter parce qu’elle ne dure pas longtemps, qu’elle contient parfois des fréquences parasites, et qu’elle n’est pas régulière, contrairement à la partie tenue. Il est donc plus difficile d’utiliser les techniques d’analyse que l’on verra par la suite.
On va donc supprimer l’attaque, même si elle est intéressante, parce que l’on ne sait travailler qu’avec le continu. Pour ce faire, on va simplement tronquer les quelques premières millisecondes du signal. Ce n’est pas très subtil, je dois bien le reconnaître, mais c’est efficace.
Fenêtrer le signal
Pour éviter quelques effets désagréables par la suite, comme le repliement de spectre, on peut appliquer une fenêtre de Hamming. Un peu plus de détails sur le pourquoi du comment ici.
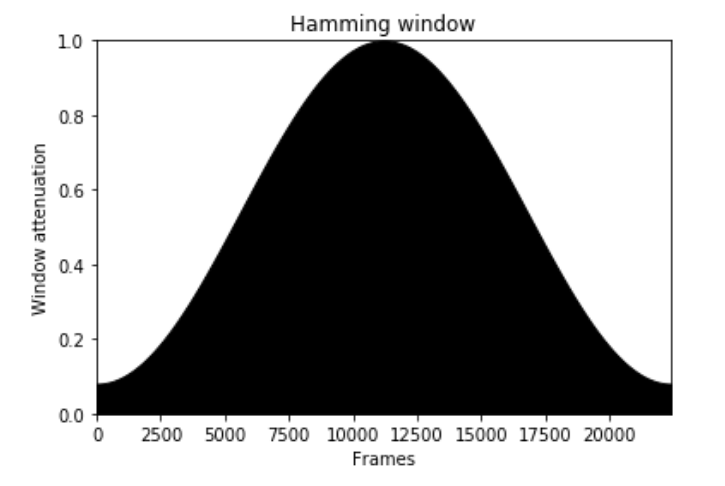
On est dans un cas très gentil où l’on arrive à bien isoler un accord, mais en pratique (dans un vrai morceau de musique) c’est beaucoup plus compliqué. Il faudrait commencer par trouver les endroits où l’on entend bien des accords, ce qui n’est pas immédiat.
Affichons pour voir un peu le résultat :

Bon, ce signal n’est pas tellement plus engageant qu’auparavant, mais il pose beaucoup moins de problèmes que celui de départ. C’est donc avec ce signal que l’on va travailler. Cependant, la représentation actuelle n’est pas pratique pour travailler, et il est à peu près impossible de déterminer les notes avec, donc il va falloir en trouver une autre. Je vous la donne en mille : la transformée de Fourier.
La transformée de Fourier
Je ne vais pas m’étendre sur la transformée de Fourier, parce qu’il y a des milliers de trucs à dire dessus, et qu’on pourrait y passer des heures, donc on va se contenter du minimum vital.
En pratique, ce n’est même pas la peine de travailler sur le signal seul : il ne donne pas les informations qui nous intéressent. La transformée de Fourier est l’outil fondamental pour le traitement de signal (même les ondelettes, ça ne fonctionne pas bien pour le son).
Le principe de la transformée de Fourier, c’est de calculer une autre représentation du signal, mais qui va être plus pratique pour savoir ce qu’il contient. Elle permet de transformer un bout de signal donné (comme ce que l’on a) en un spectre qui décrit les fréquences de ce signal.
Le spectre à plein d’avantages :
- on peut revenir au signal à partir du spectre ;
- on voit facilement les notes à partir d’un spectre ;
- il peut se calculer rapidement (avec ce que l’on appelle la FFT, la transformée de Fourier rapide).
Une transformée de Fourier nous donne un signal qui a la tête suivante : amplitude en fonction des fréquences.

À première vue, ça n’a peut-être pas l’air plus sympa que le signal vu précédemment, mais les pics donnent en fait beaucoup d’informations sur les notes présentes dans l’extrait, comme on va le voir par la suite.
Une transformée de Fourier est à valeurs dans les complexes, donc ce que l’on a affiché, c’est le module de la transformée. En plus, c’est en échelle log, parce que l’oreille humaine entend la puissance d’un son en échelle log, l’unité utilisée étant le décibel.
Le lien entre fréquences et musique
Si vous n’êtes pas totalement familier avec l’acoustique, je vous suggère d’aller faire un tour du côté du tutoriel sur les signaux sinusoïdaux de Aabu, plus particulièrement la partie . La partie n’est pas utile ici, parce qu’à l’oreille, on est incapables de percevoir la différence entre deux signaux déphasés.
Les ondes et les notes
Une note est une onde. Plus que ça, c’est une onde périodique. Et encore mieux, la fréquence de l’onde permet de déterminer la note ! Vous avez sûrement entendu parler du la : le la est la note que vous entendez en décrochant le téléphone, et c’est une onde périodique à Hertz.
Le la est la fréquence de référence qui permet d’avoir un point de repère pour accorder les instruments. Ce n’est cependant qu’une convention qui a beaucoup bougé au cours de l’histoire.
On va tout d’abord raisonner en termes d’ondes sinusoïdes, parce que ce sont les ondes les plus simples à étudier. Avec les ondes sinusoïdes, on a une onde = une note. Par exemple, une onde sinusoïdale de fréquence Hz sonnera comme un la.
Si on double la fréquence, on obtient une onde sinusoïdale de fréquence Hz. Si on joue ces deux ondes ensemble, ça sonnera bien parce qu’une onde va exactement deux fois plus vite que l’autre. On entendra une octave.
En gros, à chaque fois que l’on double la fréquence, on monte d’une octave. Avec le même raisonnement, quand on multiplie par , ça sonne très bien aussi : c’est une quinte. Ainsi, pour passer de Hz à Hz, on multiplie par la fréquence. Il se trouve que le est un mi, c’est-à-dire la quinte de la. Comme quoi, la musique n’est pas faite au hasard !
Si on pousse le vice un peu plus loin, on se rend compte que les notes sont sur une échelle logarithmique de la fréquence. On peut donc déterminer le facteur multiplicatif entre deux demi-tons successifs. Si on augmente de 12 demis-tons, soit une octave, on multiplie 12 fois la fréquence par le facteur entre deux demi-tons, pour un facteur de 2 en tout. Par conséquent, pour passer au demi-ton supérieur, il suffit de multiplier par environ ( pour être un peu plus précis, vu que ).
En pratique, c’est un petit peu plus compliqué et les choses ne se passent pas aussi bien que l’on aurait pu l’espérer. Je laisse les détails aux curieux dans la vidéo de science étonnante.
Les harmoniques
Maintenant que l’on a quelques bases, il est temps de voir ce qui se passe pour une note de musique qui sort d’un instrument.
Une note de musique jouée par un instrument est une onde périodique. Seulement, elle n’est pas aussi simple qu’une onde sinusoïdale. En fait, une note d’instrument est une somme d’ondes sinusoïdales de fréquences multiples d’une fréquence que l’on appellera fondamentale.
On a un peu idéalisé les instruments de musique en disant ça, mais c’est une approximation raisonnable, sauf pour les instruments pathologiques comme les cloches.
Par exemple, si l’on entend un la du milieu du clavier au piano (on l’appelle la), on pourra dire que c’est la somme d’une onde sinusoïdale de fréquence 440 Hz, d’une autre à 880 Hz, d’une autre à 1320 Hz, d’une autre à 1760 Hz, etc. Ces fréquences autres que la fondamentale sont appelées les harmoniques.
En théorie, on pourrait additionner les fréquences jusqu’à l’infini, mais notre oreille est limitée, ce qui fait que le commun des mortels n’entend plus grand chose après Hz. En plus, les harmoniques sont en général de plus en plus faibles donc on peut les négliger à partir d’un certain rang.
Pour les amateurs de formules, on a : la, avec l’onde sinusoïdale de fréquence , et les amplitudes des harmoniques. Pour revenir sur la remarque juste au-dessus, les est le plus souvent décroissant en fonction de .
Les harmoniques sont très importantes, car c’est justement les amplitudes des différentes harmoniques qui va déterminer le timbre d’un instrument et faire qu’on entend une différence entre un violon et une clarinette par exemple.
Vous aurez sans doute remarqué qu’avec les informations ci-dessus, on se rend compte qu’un la contient en fait d’autres notes que le la : les harmoniques ne sont pas toutes des la. Voici un petit tableau des premières harmoniques :
| Numero des harmoniques | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Intervalles | note réelle | octave | quinte | octave | tierce majeure | quinte | septième mineure | octave | seconde | tierce majeure |
| Exemple | la | la | mi | la | do | mi | sol | la | si | do |
Si un accord parfait est composé d’une note, sa quinte et sa tierce, ce n’est pas un hasard. Ça sonne bien parce que ce sont les notes des premières harmoniques. D’ailleurs, il est probable que l’accord parfait mineur sonne sombre justement parce que c’est une tierce majeure et non mineure à la harmonique.
C’est là que l’on se rend compte que la détection de notes risque d’être compliquée : si à chaque fois que l’on joue une note, il y en a plein qui viennent en bonus, ça risque d’être compliqué.
Par exemple voici la transformée de Fourier de notre signal, avec toutes les harmoniques d’une note qui sont entourées pour la note do 260. Les fréquences correspondantes sont environ les multiples de 260 :

Cependant, en pratique l’amplitude des harmoniques décroit : plus on prend des harmoniques d’ordre élevé, moins on les entend. Donc en fait, on entendra bien la fréquence fondamentale, un peu moins bien l’harmonique suivante, etc.
Cela nous donne une idée d’une approche à suivre pour détecter les notes d’un accord : on peut regarder les fréquences, détecter une note en regardant les fréquences qui ont une grande amplitude, puis supprimer cette fréquence et toutes ses harmoniques, et ensuite recommencer avec le spectre restant.
C’est une bonne idée, et c’est ce que l’on va faire. Cependant, il faut tout de suite mettre quelques points au clair :
- il faut savoir comment détecter une note de manière fiable ;
- il faut savoir comment supprimer les harmoniques ;
- on aura des problèmes pour les octaves et potentiellement les quintes, parce que si on supprime les harmoniques d’une note, on supprime aussi l’octave, parce qu’elle est contenue dans les harmoniques.
Mais on a rien sans rien, et il faut bien y aller.
Détecter une note
Allons dans le vif du sujet : la détection d’une note dans le signal.
- La mission : déterminer une note de l’accord, c’est-à-dire une fréquence fondamentale .
- Les outils : le spectre des fréquences, c’est-à-dire un tableau dont les cases sont espacées d’une fréquence .
- La description de la cible : la note se reconnaît visuellement sur le spectre par un grand pic.
La question qui se pose, c’est comment déterminer ce "grand pic".
On pourrait se dire : on regarde l’indice du tableau contenant la fréquence de plus grande amplitude. En gros, on dit : .
est le moyen simple de formaliser ce que l’on veut. Pour traduire, signifie : "le qui maximise "
Cette idée a du bon et du moins bon. Elle est ultra simple, mais elle ne garantit pas un bon résultat, parce que le monde n’est pas parfait, et que quand on détecte une fréquence, avec l’erreur de l’instrument, du détecteur, de l’échantillonnage, on peut facilement taper à côté. Il faudrait donc essayer d’avoir une méthode qui prenne un peu plus de choses en compte.
Et si on utilisait les harmoniques ?
Ça, c’est une bonne idée. Il n’y a pas que le pic de plus grande amplitude qui donne des informations sur la note, il y a aussi les pics des harmoniques. On pourrait se dire qu’un bon candidat pour a un pic en , mais également en tous les multiples de . On appelle ça la somme spectrale. Le but est donc de trouver la fréquence qui maximise :
avec qui correspond à l’indice de dans le tableau.
En pratique, on va se donner une plage de fréquences possibles, puis on va faire la somme spectrale pour chaque élément de la plage. L’élément qui donnera la plus grande valeur sera gardé.
La somme spectrale donne parfois le bon résultat à une quinte ou une octave près, c’est pourquoi on va privilégier le produit spectral, qui consiste simplement à remplacer la somme par un produit. Ainsi, nous allons chercher à déterminer :
Le critère d’arrêt
Le principe, c’est que l’on trouve une note, puis on supprime les harmoniques, et on continue jusqu’à ce qu’il n’y en ait plus.
Il est bien de détecter une note, mais il est également intéressant de savoir quand il n’y a plus de notes. Là, il n’y a pas de critère absolu. On peut se dire que lorsque le signal ne contient pas de fréquence d’amplitude "grande", on arrête de chercher.
Ce que j’ai fait, c’est prendre l’amplitude max du signal de départ comme référence, et si la note que l’on détecte a une amplitude largement inférieure à cette amplitude de référence, on considère qu’il n’y a plus de note (tout du moins de note que l’on entendrait distinctement) dans le spectre.
Supprimer la note du signal
Maintenant que l’on a pu détecter une note, il faudrait pouvoir la supprimer du spectre pour pouvoir trouver les notes suivantes en réitérant le processus. Il faut donc trouver un moyen de supprimer les harmoniques.
Détecter les harmoniques
Avant de supprimer les harmoniques, il faudrait savoir précisément où elles sont. Comme on l’a vu plus haut, pour une fréquence fondamentale , les harmoniques ont des fréquences multiples de . Cependant, on n’est pas dans le monde de Oui-Oui et les choses ne sont pas parfaites. On a dû échantillonner les fréquences donc on a une valeur approchée de , donc on multiplie l’erreur quand on multiplie. En plus, les instruments ont une fâcheuse tendance à de pas avoir exactement des harmoniques multiples de .
Par conséquent, en première approximation, c’est pas mal de prendre les multiples de , mais c’est mieux de rechercher un maximum local à côté de cette fréquence calculée. En pratique, on peut par exemple partir de l’harmonique calculée, et se décaler tant qu’un voisin a une amplitude plus grande.
Supprimer les harmoniques
Les harmoniques ne sont pas ponctuelles, elles sont un peu étalées dans le spectre, donc il faudrait supprimer les harmoniques sur des intervalles, du genre avec à déterminer.
On a envie d’avoir le plus grand possible, mais sans qu’il n’empiète sur ses voisins. Ses voisins, ce sont au mieux les demis-tons les plus proches, c’est-à-dire les fréquences qui sont à environ un facteur de . On a qu’à prendre un du genre , comme ça on sera certain de ne pas effacer des fréquences d’autres notes.
En supprimant les harmoniques, on obtient le résultat suivant : plein d’endroits où il y avait des pics auparavant sont maintenant à .

Il faut tout de même mentionner le problème des octaves : si on supprime les harmoniques, on va potentiellement supprimer les octaves de cette note. Il y a des méthodes qui essaient de prendre en compte cela, mais on ne va pas le faire, parce que c’est un peu compliqué.
Récap de l'algo
Un petit récapitulatif pour y voir plus clair :
tant que l'on détecte une note qui a une amplitude suffisemment grande:
pour chaque harmonique de la note:
supprimer l'harmonique
fin pour
fin tant que
renvoyer toutes les notes trouvées
Le résultat
Finalement, sur des extraits simples, on obtient des résultats plutôt satisfaisants.
Pour l’exemple sur lequel on travaille depuis le début :
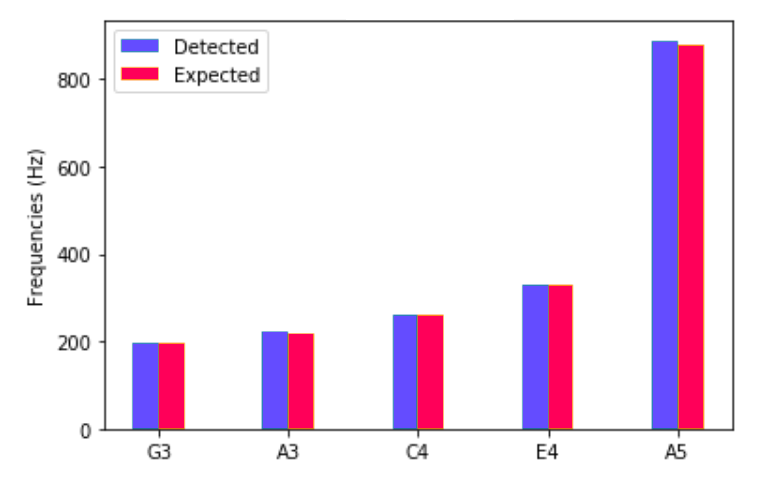
Autre exemple un peu moins réussi
Voici un autre exemple où l’on a fois la même note à des octaves différentes (lien soundcloud). On devrait réussir à trouver une note, mais il y a le problème des octaves, donc on devrait avoir du mal à trouver les trois.
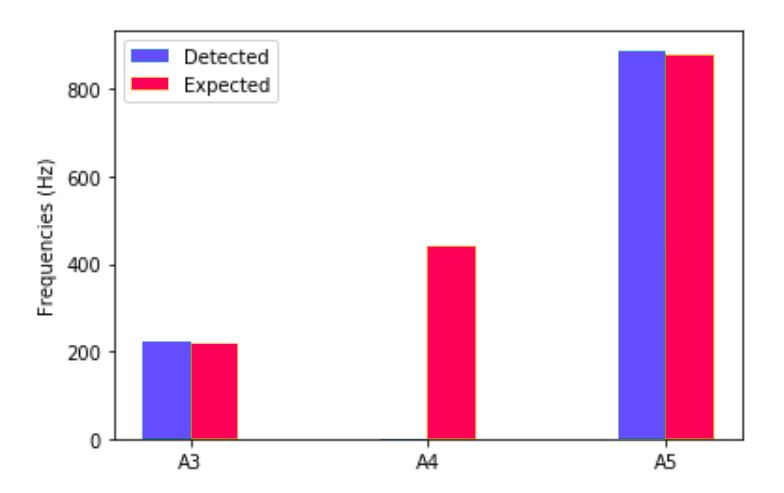
La représentation des fréquences est la suivante :

Comme on avait pu le prédire, on obtient des résultats moins bons. On a quand même réussi à récupérer octaves, mais c’est un peu un coup de chance : le A avait une plus grande amplitude que le A, et donc on l’a récupéré en premier. Par conséquent, on a pas supprimé en A en enlevant les harmoniques.
Pour le côté musical, ce n’est pas trop pénalisant de ne pas distinguer les octaves, parce que l’on raisonne de toute façon modulo l’octave. Ce qui est important, c’est surtout de savoir quelles notes composent l’accord, plus que l’ordre dans lequel elles sont agencées (excepté la basse qui a un statut un peu privilégié).
Ce petit tuto est terminé, et j’espère que vous l’avez apprécié.
Il ne faut pas oublier que l’on a travaillé sur des cas très simples, et que c’est beaucoup plus compliqué avec de vrais morceaux de musique. Cependant, cela nous a permis de travailler un peu les bases de l’analyse du signal musical.
Pour faire de la reconnaissance de manière un peu plus satisfaisante, il est maintenant commun de le faire avec du deep learning, mais c’est toujours bien (même quand on fait du deep learning) de connaître un peu ce avec quoi on travaille.
Un grand merci à Vael et etherpin pour leurs remarques pendant la rédaction et informaticienzero pour la prise en charge de la validation.








