Coefficient de partage

Dans ce tutoriel, un exercice type autour des extractions liquide-liquide sert de fil rouge pour appréhender une des facettes de la loi d’action de masse :

\mathrm{ K = \prod_{i=1}^{n} {a_i}^{\nu_i} }

Cette loi permet de comprendre les enjeux thermodynamiques autour de tout processus à l’équilibre. Souvent noté plus naïvement, pour une équation de réaction à l’équilibre :

\mathrm{ \alpha A + \beta B \rightleftarrows \gamma C + \delta D }

\mathrm{ K = \dfrac{[C]^\gamma[D]^\delta}{[A]^\alpha[B]^\beta} }

où les activités chimiques ont été remplacées naturellement par les concentrations des espèces.

Prérequis :

Connaissances autour de la constante d’équilibre $\mathrm{K}$
Connaissances autour des extractions liquide-liquide
Notions autour de la polarité des molécules

Exercice à volumes équivalents
Volumes différents
Exercice : Extraction de l'acide benzoïque

Exercice à volumes équivalents

Préambule

Je me souviens m’être souvent questionné là-dessus lors de ma première année à pratiquer la chimie. Il y a de bonnes habitudes à prendre, des concepts pas toujours simples et souvent, on ne sait pas vraiment à quel genre d’explications on doit s’attendre… On s’applique à respecter un « savoir-faire ».

Pourquoi diable devons-nous utiliser $3$ fois $\mathrm{25\;mL}$ d’un solvant organique lors des extractions liquide-liquide ? Une fois $\mathrm{75\;mL}$ ne serait pas moins contraignant ?

C’est à cette réponse que le tutoriel va répondre pas-à-pas. Prenons d’abord le cas où sobrement nous additionnons des volumes totalement équivalent. Et ensuite, essayons de mathématiser toutes les questions.

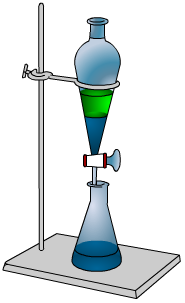
Illustration d'un montage d'extraction liquide-liquide.

Il est important, lors d’expériences d’extraction liquide-liquide de ne pas confondre ses différentes phases. Sur l’illustration, vous voyez une démarcation nette, j’ai délibérément choisi deux couleurs différentes pour illustrer les solvants non-miscibles.

Mais en réalité, la différenciation est plus complexe. Une phase organique pourra se retrouver au dessus ou en dessous de la phase aqueuse. Pour comprendre dans quelle configuration vous vous trouverez, il faut bien entendu connaître la densité de votre phase organique. L’eau étant prise pour référence pour définir la notion même de densité, il suffira de comparer la densité du solvant organique :

$\mathrm{d < 1}$  : le solvant organique est donc plus léger que l’eau, il sera porté par l’eau (au dessus) ;
$\mathrm{d > 1}$  : le solvant organique sera donc plus lourd que l’eau, il portera l’eau (au dessous) ;

Toutes les concentrations seront exprimées en $\mathrm{g\cdot L^{-1}}$ pour des raisons pratiques.

Dans le vif du sujet

Comme pour tout équilibre, nous avons une constante d’équilibre attitrée. Le tout est de poser l’équation convenablement. Pour cela, il nous faut un cas théorique :

Énoncé :

Nous avons un ballon contenant $\mathrm{V_1=75\;mL}$ d’eau contenant $\mathrm{m_1=10\;g}$ d’agent chimique $\mathrm{X}$ .

Si l’on souhaite extraire cet agent chimique $\mathrm{X}$ , il faut utiliser un solvant dans lequel cet agent sera plus soluble que dans l’eau. Ce solvant doit aussi avoir la particularité de ne pas être miscible à l’eau.

Tableau pratique des solvants d’extraction

Voici une liste des solvants couramment utilisés lors d’extraction liquide-liquide :

Nom	Formules semi-développées	Formules topologiques
Éther Diéthylique	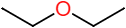$\mathrm{H_3C-H_2C-O-CH_2-CH_3}$
Dichlorométhane	$\mathrm{CH_2Cl_2}$
Éther de pétrole	-	alcanes
Éthanoate d’éthyle	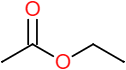$\mathrm{H_3C-COO-CH_2-CH_3}$
Toluène	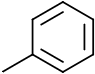$\mathrm{C_7H_8}$

On caractérise un bon solvant d’extraction en trois points :

le solvant d’extraction ne doit pas être miscible avec le solvant qui contient notre produit d’intérêt ;
le solvant doit avoir une meilleure solubilisation du produit d’intérêt que le solvant de départ ;
faible température d’ébullition, pour finalement pouvoir soustraire le solvant du mélange obtenu.

Équations

Imaginons que nous choisissions le dichlorométhane (DCM), la solubilisation se produira tel que :

\mathrm{ X_{(aq)} \rightleftarrows X_{(DCM)} }

Ainsi, la loi d’action de masse s’écrit :

\mathrm{ K = \dfrac{[X_{(DCM)}]}{[X_{(aq)}]} }

Rappel :

Cette loi détermine une constante d’équilibre $\mathrm{K}$ qui ne varie que si la température ou la nature des composés évoluent. La valeur ainsi obtenue est donc conservée et réutilisée à travers l’exercice.

C’est parti

Après avoir compris les étapes qui vous permettront de mieux comprendre ces exercices, vous allez être capable de digérer un vrai énoncé, comme il se doit :

Énoncé complet :

Résolution pas-à-pas

Nous repartons de l’équation de $\mathrm{K}$  :

\mathrm{ K = \dfrac{[X_{(DCM)}]}{[X_{(aq)}]} = 2 }

Les concentrations massiques peuvent se développer selon : $\mathrm{[X] = \dfrac{m_X}{V}}$

\mathrm{ \dfrac{m_{DCM}/V_2}{m_{aq}/V_1} = 2 }

On sait aussi, que peu importe le comportement des solutions, nous retrouverons en tout et pour tout les $\mathrm{10\;g}$ d’agent chimique X mis en jeu. Cela se traduit par :

\mathrm{ m_{DCM} + m_{aq} = 10\;g }

Si bien qu’en ayant un regard un peu entraîné, on voit clairement que $\mathrm{V_1=V_2}$ et ainsi une partie de l’équation se simplifie :

\mathrm{ \dfrac{m_{DCM}}{m_{aq}} = 2 }

Nous avons donc le système d’équations suivant :

\mathrm{ \left\{\begin{aligned} m_{DCM} + m_{aq} &= 10\;g \\ \dfrac{m_{DCM}}{m_{aq}} &= 2 \\ \end{aligned}\right. }

\mathrm{ \left\{\begin{aligned} m_{DCM} + m_{aq} &= 10\;g \\ m_{DCM} &= 2\;m_{aq} \\ \end{aligned}\right. }

\mathrm{ 2\;m_{aq} + m_{aq} = 10\;g }

Finalement on obtient l’expression triviale :

\mathrm{ 3\;m_{aq} = 10\;g }

Ainsi, nous savons que $\mathrm{m_{aq}}$ vaut $3{,}333...333...\;g$ . Et par correspondance, $\mathrm{m_{DCM}=10-3{,}333...333... = 6{,}666...666...\;g}$ .

La réponse est donc :

En une seule extraction, nous avons obtenu $6{,}66\;g$ d’agent chimique $\mathrm X$ .

Nous avons un rendement d’extraction de $\mathrm{67\%}$  ! C’est une valeur qui aura son importance dans la prochaine partie, donc soyez attentif.

Volumes différents

Préambule

Cette fois-ci, essayons le traditionnel «  $3$ fois $\mathrm{25\;mL}$  ». C’est très courant de croiser cette démarche opératoire dans les laboratoires de chimie organique. Même si en pratique les volumes d’extraction sont vraiment très peu souvent précisés dans les modes opératoires. On se contentera d’extraire une phase aqueuse avec $1/3$ de solvant organique, le tout $3$ fois.

Là, notre but sera simplement mathématique, nous chercherons à comparer les méthodes en une seule extraction ou bien en trois extractions. Ainsi, on montrera que :

\mathrm{ f(75) \neq 3 \times f(25) }

On dit alors que ces équations ne sont pas des combinaisons linéaires. L’idée est donc d’utiliser la même solution de départ, mais au lieu de lancer l’extraction une fois pour toute, nous allons essayer de repartir en $3$ ajouts successifs le solvant à haut potentiel solubilisant.

Énoncé :

Dans un ballon, nous avons $\mathrm{V_1=75\;mL}$ d’eau dans lesquels il y a $\mathrm{m_1=10\;g}$ de soluté X. Le mélange est transvasé dans une ampoule à décanter dans le but de procéder à une extraction liquide-liquide. $\mathrm{V_2=25\;mL}$ de DCM sont alors ajoutés à l’ampoule. L’ampoule est agitée et dégazée à plusieurs reprises. La phase aqueuse est alors récupérée et ré-extraite de cette manière, avec $\mathrm{V_2=25\;mL}$ de DCM vierge une fois encore, pour à la fin avoir extrait $3$ fois la phase aqueuse, avec un total de phase organique de $\mathrm{75\;mL}$ . Sachant que $\mathrm{K = 2}$ , combien d’agent chimique X sera extrait à la fin des $3$ brassages ?

$1^{ère}$ extraction

Nous repartons de l’équation de $\mathrm{K}$  :

\mathrm{ K = \dfrac{[X_{(DCM)}]}{[X_{(aq)}]} = 2 }

Les concentrations massiques peuvent se développer selon : $\mathrm{[X] = \dfrac{m_X}{V}}$

\mathrm{ \dfrac{m_{DCM}/V_2}{m_{aq}/V_1} = 2 }

On sait aussi que, peu importe le comportement des solutions, nous retrouverons en tout et pour tout les $\mathrm{10\;g}$ d’agent chimique X mis en jeu. Cela se traduit par :

\mathrm{ m_{DCM} + m_{aq} = 10\;g }

Cette fois-ci, $\mathrm{V_1 \neq V_2}$ . Il faut donc trouver un rapport entre les volumes, du genre $\mathrm{V_1 = 3\;V_2}$  :

\mathrm{ \dfrac{m_{DCM}/V_2}{m_{aq}/3\;V_2} = 2 }

Nous avons donc le système d’équations suivant :

\mathrm{ \left\{\begin{aligned} m_{DCM} + m_{aq} &= 10\;g \\ \dfrac{m_{DCM}/V_2}{m_{aq}/3\;V_2} &= 2 \\ \end{aligned}\right. }

\mathrm{ \left\{\begin{aligned} m_{DCM} &= 10 - m_{aq} \\ \dfrac{3\;m_{DCM}}{m_{aq}} &= 2 \\ \end{aligned}\right. }

\mathrm{ 3\;m_{DCM} = 2m_{aq} }

\mathrm{ 30 - 3\;m_{aq} = 2m_{aq} }

\mathrm{ 30 = 5m_{aq} }

Finalement, on obtient l’expression finale :

\mathrm{ \dfrac{30}{5} = m_{aq} }

\mathrm{ m_{aq} = 6\;g }

Enfin, la masse d’agent X dans le dichlorométhane est :

\mathrm{ m_{DCM} = 10 - 6 = 4\;g }

Donc à présent nous avons un petit ballon contenant $\mathrm{25\;mL}$ d’une solution d’agent chimique X, soit $\mathrm{4\;g}$ de soluté dans les $\mathrm{25\;mL}$ de solvant. Mais nous ne nous arrêterons pas là !

$2^e$ extraction

Nous repartons de l’équation de $\mathrm{K}$  :

\mathrm{ K = \dfrac{[X_{(DCM)}]}{[X_{(aq)}]} = 2 }

Les concentrations massiques peuvent se développer selon : $\mathrm{[X] = \dfrac{m_X}{V}}$

\mathrm{ \dfrac{m_{DCM}/V_2}{m_{aq}/V_1} = 2 }

Attention cette fois, nous n’avons que $\mathrm{6\;g}$ dans la phase aqueuse, nous devons donc en tenir compte ainsi :

\mathrm{ m_{DCM} + m_{aq} = 6\;g }

Encore une fois, $\mathrm{V_1 \neq V_2}$ , donc $\mathrm{V_1 = 3\;V_2}$  :

\mathrm{ \dfrac{m_{DCM}/V_2}{m_{aq}/3\;V_2} = 2 }

Nous avons donc le système d’équations suivant :

\mathrm{ \left\{\begin{aligned} m_{DCM} + m_{aq} &= 6\;g \\ \dfrac{m_{DCM}/V_2}{m_{aq}/3\;V_2} &= 2 \\ \end{aligned}\right. }

\mathrm{ \left\{\begin{aligned} m_{DCM} &= 6 - m_{aq} \\ \dfrac{3\;m_{DCM}}{m_{aq}} &= 2 \\ \end{aligned}\right. }

\mathrm{ 3\;m_{DCM} = 2m_{aq} }

\mathrm{ 18 - 3\;m_{aq} = 2m_{aq} }

\mathrm{ 18 = 5m_{aq} }

Finalement, on obtient l’expression finale :

\mathrm{ \dfrac{18}{5} = m_{aq} }

\mathrm{ m_{aq} = 3.6\;g }

Enfin, la masse d’agent X dans le dichlorométhane est :

\mathrm{ m_{DCM} = 6 - 3.6 = 2.4\;g }

Donc à présent nous avons un ballon contenant $\mathrm{50\;mL}$ d’une solution d’agent chimique X, soit $\mathrm{4+2.4= 6.4\;g}$ de soluté dans les $\mathrm{50\;mL}$ de solvant. Une dernière fois les copains !

$3^e$ extraction

Nous repartons de l’équation de $\mathrm{K}$  :

\mathrm{ K = \dfrac{[X_{(DCM)}]}{[X_{(aq)}]} = 2 }

Les concentrations massiques peuvent se développer selon : $\mathrm{[X] = \dfrac{m_X}{V}}$

\mathrm{ \dfrac{m_{DCM}/V_2}{m_{aq}/V_1} = 2 }

Attention cette fois, nous n’avons que $\mathrm{3.6\;g}$ dans la phase aqueuse, il nous faut donc en tenir compte ainsi :

\mathrm{ m_{DCM} + m_{aq} = 3.6\;g }

Encore une fois, $\mathrm{V_1 \neq V_2}$ , donc $\mathrm{V_1 = 3\;V_2}$  :

\mathrm{ \dfrac{m_{DCM}/V_2}{m_{aq}/3\;V_2} = 2 }

Nous avons donc le système d’équations suivant :

\mathrm{ \left\{\begin{aligned} m_{DCM} + m_{aq} &= 3.6\;g \\ \dfrac{m_{DCM}/V_2}{m_{aq}/3\;V_2} &= 2 \\ \end{aligned}\right. }

\mathrm{ \left\{\begin{aligned} m_{DCM} &= 3.6 - m_{aq} \\ \dfrac{3\;m_{DCM}}{m_{aq}} &= 2 \\ \end{aligned}\right. }

\mathrm{ 3\;m_{DCM} = 2m_{aq} }

\mathrm{ 10.8 - 3\;m_{aq} = 2m_{aq} }

\mathrm{ 10.8 = 5m_{aq} }

Finalement, on obtient l’expression finale :

\mathrm{ \dfrac{10.8}{5} = m_{aq} }

\mathrm{ m_{aq} = 2.16\;g }

Enfin, la masse d’agent X dans le dichlorométhane est :

\mathrm{ m_{DCM} = 3.6 - 2.16 = 1.44\;g }

Conclusion des trois extractions

Donc à présent nous avons un ballon contenant $\mathrm{75\;mL}$ d’une solution d’agent chimique X. Additionnons chacun des résultats d’extraction :

Au total, les trois extractions sont comptabilisées.

\mathrm{4+2.4+1.44= 7.85\;g}

Nous avons donc $\mathrm{7.85\;g}$ de soluté dans les $\mathrm{75\;mL}$ de solvant. Ce qui nous donne un rendement d’extraction de $\mathrm{78\%}$ pour au final, $\mathrm{75\;mL}$ de dichlorométhane !

Avec la même quantité de solvant, $\mathrm{75\;mL}$ de dichlorométhane dans les deux méthodes, on est passé d’un rendement de $\mathrm{63\%}$ à $\mathrm{78\%}$ .

Conclusion générale et perspective

Ce qu’il faut retenir

Donc plus on subdivise les extractions, plus c’est rentable d’extraire. En tout cas par rapport à la pseudo-méthode « j’mets tout d’un coup là-bas dedans »…

En théorie, il faudrait même mettre $\mathrm{1\;mL}$ par extraction, mais faire ça $75$ fois ! Bon en réalité personne ne fera ça en laboratoire…

En pratique, les gouttes se perdraient sur les contours des verreries et la perte serait potentiellement trop importante.

Comment nettoyer sa verrerie ?

Il est donc préférable de faire couler un filet d’eau distillée (ou d’acétone) et de ne pas laisser la verrerie se remplir. Faire $4$ giclées de solvant en étant sûre que les parois soient rincées est préférable à « remplir la verrerie jusqu’à sa moitié et la vider… et recommencer ».

Pour les mêmes raisons, il vaut mieux rincer avec peu de solvant plusieurs fois, sachant que le solvant par à la poubelle ensuite, il en va d’une question d’écologie et d’économie .

Exercice : Extraction de l'acide benzoïque

Cette fois-ci je vais vous laissez vous entraîner tranquillement. La méthode à été élargie, comprise, maintenant l’intérêt est de se l’approprier. Nous traiterons maintenant de l’acide benzoïque initialement solubilisé dans de l’eau.

Malheureusement l’élève qui a solubilisé l’acide benzoïque Ô tant convoité, n’a pas utilisé d’eau distillé. La solution est donc contaminée par une flopée de sels divers et variés nuisant à l’utilisation de l’acide benzoïque .

C’est donc à vous de trouver la meilleure solution pour extraire l’acide benzoïque…

Vous disposez de $\mathrm{10\;g}$ d’acide benzoïque dans une eau contaminée par des sels. Ces derniers ne sont pas solubles dans le toluène. Il est alors intéressant de procéder à l’extraction des $\mathrm{100\;mL}$ de solution aqueuse par $2$ fois $\mathrm{50\;mL}$ de toluène. Sachant que $\mathrm{K=6}$ , quel est le rendement d’extraction global ?

$\mathrm{m_{tol1}=7,5\;g}$

$\mathrm{m_{tol2}=1,875\;g}$

$\mathrm{m_{tol}=9,375\;g}$

$\mathrm{94\%}$

J’espère que ce cas d’école aura répondu à certaines de vos questions. Peut-être ne vous vous étiez pas formulé ainsi les questions, mais si vous avez déjà pratiqué la chimie, ces questionnements ont forcément fait leur apparition.

Rédaction : @Blackline
Illustration : @Blackline
Relecture pédagogique : @Pierre_24
Validation : @Qwerty

Exercice à volumes équivalents

Préambule

Dans le vif du sujet

Tableau pratique des solvants d’extraction

Équations

C’est parti

Résolution pas-à-pas

Volumes différents

Préambule

$1^{ère}$ extraction

$2^e$ extraction

$3^e$ extraction

Conclusion des trois extractions

Conclusion générale et perspective

Ce qu’il faut retenir

Comment nettoyer sa verrerie ?

Exercice : Extraction de l'acide benzoïque

1 commentaire

Pas encore membre ?

Exercice à volumes équivalents

Préambule

Dans le vif du sujet

Tableau pratique des solvants d’extraction

Équations

C’est parti

Résolution pas-à-pas

Volumes différents

Préambule

1eˋre1^{ère}1eˋre extraction

2e2^e2e extraction

3e3^e3e extraction

Conclusion des trois extractions

Conclusion générale et perspective

Ce qu’il faut retenir

Comment nettoyer sa verrerie ?

Exercice : Extraction de l'acide benzoïque

1 commentaire

Pas encore membre ?

$1^{ère}$ extraction

$2^e$ extraction

$3^e$ extraction

Comment nettoyer sa verrerie ?