L’astronomie antique

Les astronomes antiques babyloniens, assyriens et égyptiens connaissaient la durée approximative de l’année. Les Égyptiens, par exemple, ont adopté il y a 3000 ans un calendrier basé sur une année de 365 jours. Ils suivaient avec attention le moment de lever avant l’aube de l’étoile Sirius, qui a un cycle annuel correspondant à l’inondation du Nil. Les Chinois avaient aussi un calendrier fonctionnel ; ils ont déterminé la durée de l’année à la même période que les Égyptiens. Les Chinois ont aussi noté des comètes, des météores brillants et les taches sombres du Soleil¹. Plus tard, les astronomes Chinois ont conservé des enregistrements détaillés d’« étoiles invitées » – qui sont normalement trop faibles pour être vues, mais qui s’illuminent soudain pour devenir visible à l’œil nu pour quelques semaines ou mois. Nous utilisons toujours certains de ces documents pour étudier des étoiles qui ont explosé il y a longtemps.

La culture Maya, au Mexique et en Amérique Centrale, a développé un calendrier sophistiqué basé sur la planète Vénus. Ils ont construit des sites dédiés à l’observation astronomique il y a plus de mille ans. Les Polynésiens maitrisaient la navigation aux étoiles, une compétence qui leur a permis de parcourir des centaines de kilomètres au large sur l’océan et de coloniser des îles très éloignées de leur point de départ.

En Grande-Bretagne, avant que l’usage de l’écriture ne se répande, les peuples antiques utilisaient des pierres pour conserver une trace des trajectoires du Soleil et de la Lune. Il existe toujours certains des grands cercles qu’ils ont construit à cet effet, et qui datent d’aussi loin que 2800 avant notre ère. Le plus connu est Stonehenge, qui sera étudié dans La Terre, la Lune et le Ciel ².

Notre concept du cosmos – sa structure de base et son origine – est appelé cosmologie, un mot aux racines grecques. Avant l’invention des télescopes, les seuls indices accessibles aux humains quant au fonctionnement de l’univers passaient par leurs sens. Nos ancêtres ont développé des cosmologies qui combinaient leurs observations directes des cieux avec une riche variété de symbolisme philosophique et religieux.

Au moins 2000 ans avant Christophe Colomb, les personnes éduquées de l’Est méditerranéen savaient que la Terre était ronde. La théorie d’une Terre sphérique remonte peut-être au temps de Pythagore, un philosophe et mathématicien qui vivait il y a 2500 ans. Il pensait que les cercles et les sphères étaient des « formes parfaites » ; et suggérait donc que la Terre devait être une sphère. Comme preuve que les dieux aimaient les sphères, les Grecs citaient le fait que la Lune en est une, via une preuve que nous étudierons plus loin.

Les écrits d’Aristote (384–322 avant JC), le tuteur d’Alexandre le Grand, résument la majorité de ces idées. Ils décrivent comment la progression des phases de la Lune – son changement de forme apparent – proviennent de notre vision de différentes parties de l’hémisphère éclairé de la Lune au fur et à mesure de son déplacement (cf La Terre, la Lune et le Ciel). Aristote savait aussi que le Soleil devait être plus loin de la Terre que la Lune, car de temps à autres cette dernière passe exactement entre la Terre et le Soleil et le masque temporairement. Ce phénomène est appelé éclipse de Soleil.

Aristote citait des preuves convaincantes que la Terre devait être ronde. La première est le fait que, lorsque la Lune entre ou sort de l’ombre de la Terre lors d’une éclipse de Lune, la forme de l’ombre vue sur la Lune est toujours ronde (Figure 2.9). Seul un objet sphérique provoque toujours des ombres rondes. Si la Terre était un disque, par exemple, il y aurait des cas où la lumière du Soleil la frapperait par le côté et où son ombre sur la Lune serait une ligne.

Comme seconde preuve, Aristote expliquait que les voyageurs qui allaient loin au sud pouvaient observer des étoiles invisibles plus au nord, et que la hauteur de l’Étoile Polaire – l’étoile la plus proche du pôle céleste Nord – diminuait d’autant plus que le voyageur était au sud. La seule explication possible était que le voyageur se déplace sur une surface courbe, montrant les étoiles sous un angle différent. D’autres preuves de la rotondité de la Terre sont présentées dans l’encart « Comment savons-nous que la Terre est ronde ? » ci-dessous.

Un penseur Grec, Aristarque de Samos (310 - 230 avant JC) a même suggéré que la Terre tournait autour du Soleil, mais Aristote et la plupart des savants Grecs antiques ont rejeté cette idée. Une de leurs raisons de leur conclusion était que, si la Terre tournait autour du Soleil, ils devraient observer les étoiles dans des positions différentes au cours de l’orbite de la Terre. Lors du déplacement de la Terre, les positions des étoiles les plus proches devraient varier par rapport aux étoiles les plus lointaines. D’une façon similaire, lors que nous nous déplaçons, nous voyons les objets en premier plan bouger par rapport aux objets plus lointains en arrière-plan. Lorsque nous voyageons en train, les arbres du premier-plan semblent changer de position par rapport aux collines distantes, au fur et à mesure que le train roule. Nous utilisons ce phénomène de façon inconsciente pour estimer les distances.

Ce changement apparent de direction d’un objet dû au déplacement de l’observateur est appelé parallaxe. Nous appelons parallaxe stellaire¹ le changement dans la direction apparente d’une étoile provoqué par le mouvement orbital de la Terre. Les Grecs ont fait des efforts spécifiques pour observer la parallaxe stellaire, allant jusqu’à enrôler à cet effet les soldats dotés de la meilleure vision, mais sans résultats. Les étoiles les plus brillantes (et à priori les plus proches) ne semblaient pas se déplacer lorsque les Grecs les observaient au printemps et à l’automne (lorsque la Terre est de l’autre côté du Soleil).

Ceci impliquait soit que la Terre ne se déplaçait pas, soit que les étoiles étaient à des distances si titanesques que les décalages dus à la parallaxe étaient d’une petitesse immensurable. Un cosmos si gigantesque impliquait un saut d’imagination que les philosophes antiques n’étaient pas préparés à faire, c’est pourquoi ils préférèrent rester sur la sûreté d’un modèle géocentrique, qui domina la culture occidentale pour presque deux millénaires.

Non seulement les Grecs savaient que la Terre est ronde, mais ils étaient aussi capable d’en mesurer la taille. La première mesure plutôt précise du diamètre de la Terre a été réalisée vers 200 avant JC par Ératosthène (276 - 194 avant JC), un Grec qui vivait à Alexandrie en Égypte.

Le Soleil est si éloigné de nous que ses rayons, lorsqu’ils nous atteignent, peuvent être considérés comme parallèles. Pour comprendre pourquoi, voyez la figure 2.10. Prenons une source de lumière proche de la Terre – disons, en position A. Ses rayons frappent différents endroits de la Terre sous des angles différents. Depuis une source de lumière B ou C (qui sont plus éloignées de la Terre), l’angle entre les rayons qui frappent des points opposés de la Terre est plus petit. Plus la source est distante, plus l’angle est petit ; pour une source à l’infini, les rayons voyagent sur des droites parallèles.

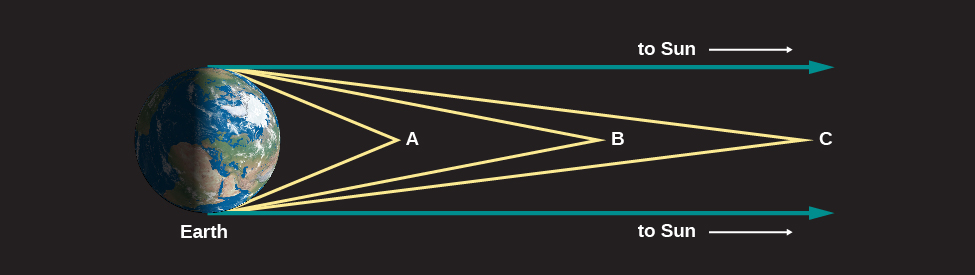
Évidemment, le Soleil n’est pas infiniment loin, mais à une distance de 150 millions de kilomètres. Lorsqu’ils frappent la Terre, ses rayons divergent d’un angle trop petit pour être visible à l’œil nu. En conséquence, si toutes les personnes du monde pouvaient pointer le Soleil en même temps, leurs doigts seraient essentiellement tous parallèles¹.

Ératosthène savait que, le premier jour de l’été à Syène en Égypte (actuellement Assouan), à midi, le Soleil éclairait le fond d’un puits vertical. Ceci signifiait que le Soleil était directement au-dessus du puits – et donc que Syène était sur une ligne qui reliait le centre de la Terre au Soleil. À une date et une heure équivalentes, à Alexandrie, Ératosthène observa l’ombre d’une colonne et constata que le Soleil n’était pas exactement à la verticale, mais légèrement au sud du zénith, de façon à ce que les rayons fassent un angle d’environ $\frac{1}{50}$ de cercle (7°). Puisque les rayons du Soleil frappant les deux villes sont parallèles entre eux, pourquoi ces rayons ne feraient-ils pas le même angle avec la surface de la Terre ? Ératosthène partit du principe que, à cause de la courbure de la Terre, « la verticale » n’indiquait pas la même direction dans les deux villes. Une conséquence de ceci, c’est que la mesure de l’angle entre le rayon du Soleil et la verticale à Alexandrie lui permettait de mesurer la taille de la Terre : une Terre ronde impliquait que Alexandrie devait se situer à $\frac{1}{50}$ de circonférence terrestre au nord de Syène (Figure 2.11). Une mesure indiquait qu’Alexandrie se situait à 5000 stades² au nord de Syène, et donc que la circonférence de la Terre devait être de $50 \times 5000$ soit 250 000 stades.

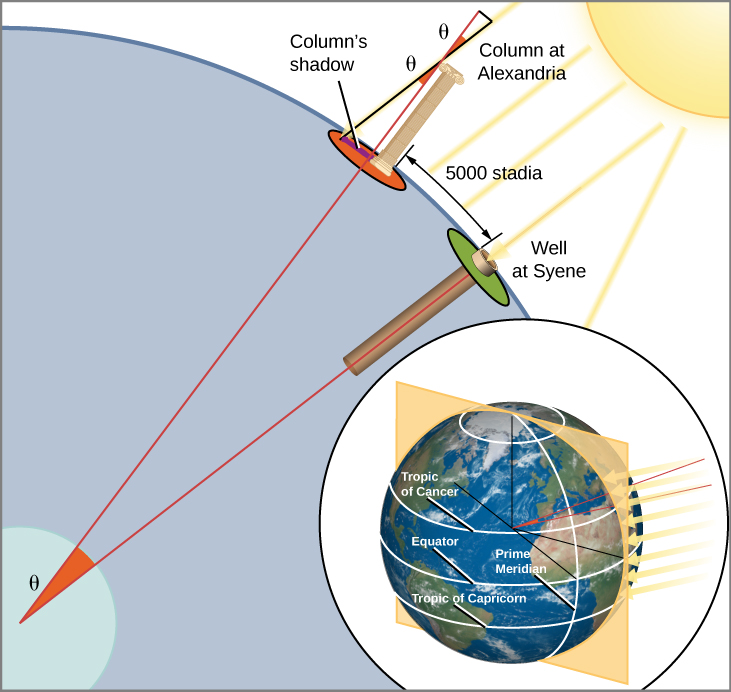
Il est impossible d’évaluer avec exactitude la précision de la mesure d’Ératosthène, parce qu’il y a un doute sur la longueur exact du stade qu’il utilisait comme unité de distance. S’il utilisait le stade grec d’Olympie, son résultat est trop grand d’environ 20 % ; mais s’il utilisait un stade égyptien, sa mesure est exacte à 1 % près (39 375 km mesurés pour 40 007,864 km pour un méridien passant par les pôles). Cela dit, même si sa mesure n’était pas exacte, sa réussite à mesurer la taille de notre planète uniquement à l’aide d’ombres, de rayons du Soleil et du pouvoir de la pensée humain est l’une des plus grandes réalisations intellectuelles de l’histoire.

Le plus grand astronome de l’antiquité était peut-être Hipparque, né à Nicée dans l’actuelle Turquie. Il a construit un observatoire sur l’ile de Rhodes autours de 150 avant JC, pendant l’expansion de l’influence de la République romaine autour de la Méditerranée. Là, il mesura avec la meilleure précision possible la position d’objets célestes. Il compila ainsi le premier catalogue d’étoiles, qui contenait environ 850 éléments. Il a désigné des coordonnées célestes pour chacune de ces étoiles, spécifiant leurs positions dans le ciel de la même manière que nous spécifions la position d’un point sur Terre par sa latitude et sa longitude.

Il divisa aussi les étoiles en magnitudes apparentes selon leur luminosité apparente. Il appela les plus brillantes « étoiles de première magnitude », le groupe suivant en terme de brillance « étoiles de seconde magnitude », et ainsi de suite. Ce système arbitraire, bien que modifié, est toujours utilisé aujourd’hui – même s’il est de moins en moins utile pour les astronomes professionnels.

En observant les étoiles et en comparant ses données avec des observations plus anciennes, Hipparque fit l’une de ses découvertes les plus remarquables : la position dans le ciel du pôle céleste nord avait changé au cours du siècle et demi passé. Hipparque en déduisit, à raison, que ce phénomène ne s’était pas produit seulement pendant cette période d’observation, mais en réalité existait tout le temps. Rappelons ici que le pôle nord céleste est simplement la projection du pôle nord terrestre dans le ciel. Si le pôle nord céleste vacille, alors la Terre elle-même doit vaciller. Aujourd’hui, nous savons qu’en effet, la direction dans laquelle l’axe de la Terre pointe change dans un mouvement lent et régulier, appelé précession. Si vous avez déjà regardé une toupie tourner, vous avez observé un mouvement similaire : l’axe vertical décrit un chemin qui forme un cône (Figure 2.12).

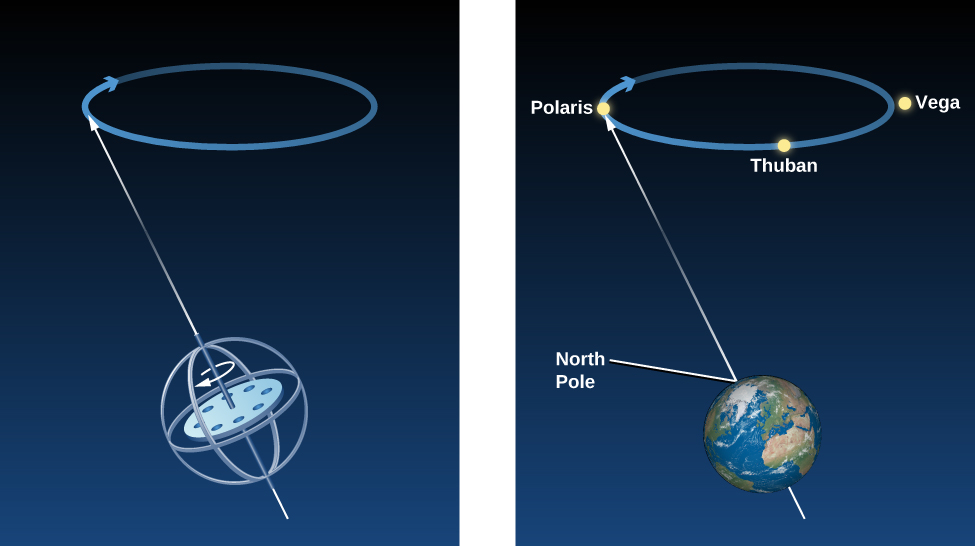
Parce que notre planète n’est pas exactement une sphère mais est un peu plus large à l’équateur, l’attraction du Soleil et de la Lune la font vaciller comme une toupie. Il faut environ 26 000 ans à l’axe de la Terre pour compléter un cercle de précession. En conséquence de ce mouvement, le point pointé par notre axe dans le ciel change au cour du temps. Alors que Alpha de la Petite Ourse (ou Polaris, ou l’Étoile Polaire) est l’étoile la plus proche du pôle nord céleste aujourd’hui (elle en sera le plus proche vers 2100), Véga (dans la constellation de la Lyre) sera l’étoile polaire dans 14 000 ans.

Le dernier grand astronome de la Rome antique était Claude Ptolémée (ou simplement Ptolémée), qui réalisa ses plus grands travaux aux alentours de l’an 140 de notre ère, à Alexandrie en Égypte. Il réalisa une grande compilation de connaissances astronomiques, aujourd’hui connue sous le nom d’Almageste (d’après une arabisation d’un terme grec ancien signifiant « La Grande Composition »). L’Almageste ne contient pas seulement des travaux originaux de Ptolémée, mais aussi une étude des réalisations astronomiques passées, principalement celles d’Hipparque. C’est aujourd’hui notre principale source d’information sur les travaux de ce dernier et d’autres astronomes de la Grèce antique.

La contribution la plus importante de Ptolémée a été sa représentation géométrique du système solaire, capable de prédire la position des planètes pour n’importe quelle date. Hipparque n’avait pas assez de données pour résoudre ce problème lui-même, aussi il a accumulé des observations pour la postérité. Ptolémée a complété ce matériau avec de nouvelles observations et a construit un modèle cosmologique qui a duré plus de mille ans, jusqu’à l’arrivée de Copernic.

Le facteur le plus complexe à expliquer dans le mouvement des planètes est leur errance apparente dans le ciel, qui est le résultat de la combinaison de leur mouvement propre et du mouvement orbital de la Terre. Regarder les planètes depuis notre point de vue sur une Terre en mouvement, c’est un peu comme regarder une course automobile en tant que participant : parfois la voiture d’un concurrent vous dépasse, mais parfois vous les dépassez, ce qui les fait sembler reculer par rapport à vous le temps du dépassement.

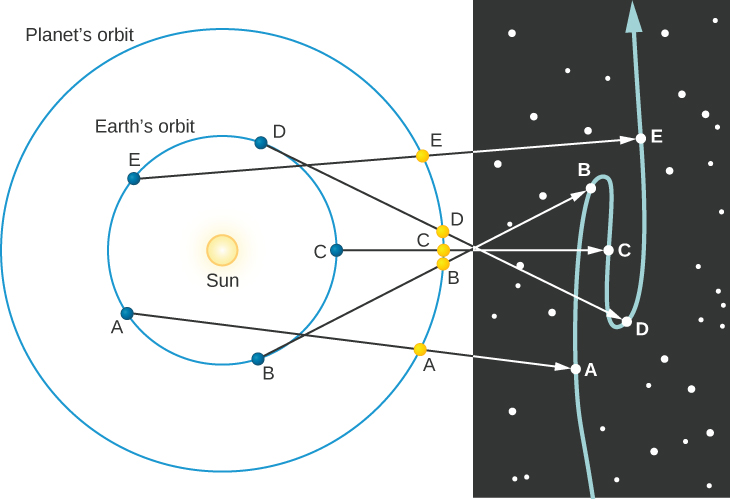
La Figure 2.13 montre le mouvement de la Terre et d’une planète plus éloignée du Soleil – ici, Mars. La Terre voyage autour du Soleil dans la même direction et presque sur le même plan que l’autre planète, mais sa vitesse orbitale est plus élevée. En conséquence, elle dépasse périodiquement la planète, comme une voiture de course sur le côté intérieur d’un virage. La figure montre où se trouve la planète dans le ciel à différents moments. Le chemin de la planète par rapport aux étoiles est présenté à droite de la figure.

Normalement, les planètes se déplacent vers l’est dans le ciel au cours des semaines et des mois, alors qu’elles orbitent autour du Soleil. Mais il arrive que, comme entre les positions B et D de notre exemple en Figure 2.13, elles semblent dériver en arrière et revenir vers l’ouest, lorsque la Terre dépasse la planète. Même si elle se déplace en réalité vers l’est, la Terre, plus rapide, la double et semble, depuis notre position, la laisser sur derrière. Lorsque la Terre atteint la position E sur son orbite, la planète reprends son mouvement apparent vers l’Est dans le ciel. Le mouvement apparent d’une planète vers l’ouest lorsque la Terre passe entre elle et le Soleil est appelé mouvement rétrograde. Un tel mouvement est simple à comprendre de nos jours, maintenant que nous savons que la Terre est l’une des planètes, qu’elle orbite autour du Soleil et qu’elle n’est pas le centre immobile de la Création. Mais Ptolémée a du faire face à un problème bien plus complexe, celui d’expliquer ces mouvements rétrogrades tout en supposant une Terre immobile.

En outre, les Grecs pensaient que les mouvements célestes étaient circulaires. Ptolémée a donc dû construire son modèle en utilisant seulement des cercles. C’est pour ça qu’il a eu besoin de dizaines de cercles, certains tournant autour d’autres cercles, dans une structure complexe qui rend confus le spectateur moderne. Mais nous ne devons pas laisser notre jugement moderne ternir notre admiration pour la réalisation de Ptolémée : à cette époque, un univers complexe centré sur la Terre était parfaitement raisonnable et, à sa manière, assez beau. Cependant, comme l’aurait dit le roi de Castille Alphonse X après s’être fait expliquer le système de mouvement des planètes : « Si le Seigneur Tout-Puissant m’avait consulté avant de commencer sa Création, je lui aurais conseillé quelque chose de plus simple ».

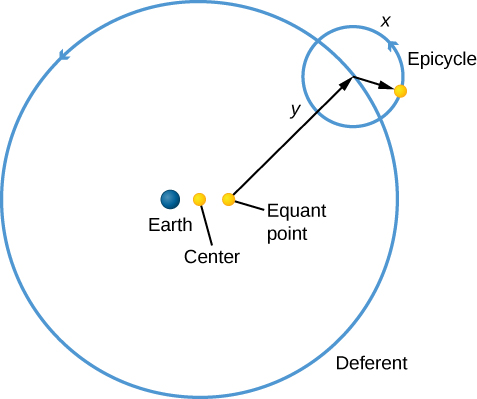
Ptolémée a résolu le problème du mouvement observé des planètes en plaçant chacune d’elle sur une petite orbite appelée épicycle. Le centre de l’épicycle tourne autour de la Terre selon un cercle appelé déférent (Figure 2.14). Lorsque la planète est dans la position x sur la Figure 2.14 de l’orbite épicycle, elle bouge dans la même direction que le centre de l’épicycle ; depuis la Terre, elle semble bouger vers l’est. À l’inverse, lorsqu’elle est dans la position y, elle se déplace autour de la Terre en sens inverse du centre de l’épicycle. En choisissant la bonne combinaison de vitesses et de distances, Ptolémée a réussi à modéliser des planètes qui se déplacent vers l’ouest à la bonne vitesse, sur la bonne distance et pendant la bonne durée. Il a donc réussi à expliquer le mouvement rétrograde avec son modèle.

Cependant, nous verrons dans Orbites et gravité que les planètes, dont la Terre, voyagent autour du Soleil sur des orbites qui sont des ellipses et non des cercles. Leur comportement réel ne peut pas être représenté avec précision par un ensemble de mouvement circulaires uniformes. Pour correspondre aux mouvements observés des planètes, Ptolémée a du centrer les cercles déférents sur un point éloigné de la Terre, et pas sur la Terre elle-même. De plus, il a introduit un mouvement circulaire uniforme autour d’encore un autre axe appelé point équant. Tout ceci a considérablement complexifié son modèle.

Le génie mathématique remarquable de Ptolémée lui a permis de développer un système aussi complexe pour modéliser, avec succès, le mouvement observé des planètes. Il est possible que le but de Ptolémée ne fût pas de concevoir un modèle cosmologique qui représente la réalité, mais seulement un outil mathématique qui lui aurait permis de prédire les positions des planètes à n’importe quelle date. Quoiqu’il en soit, ce modèle – un peu modifié – a finalement été accepté comme faisant autorité dans le monde musulman, puis plus tard en Europe chrétienne.