Les lois du mouvement planétaire

Tycho Brahe naquit dans une famille de la noblesse danoise trois ans après la publication du De Revolutionibus de Copernic. Il s’intéressa très tôt à l’astronomie et, jeune homme, fit des observations astronomiques importantes. Parmi celles-ci, une étude minutieuse de ce que nous savons aujourd’hui être une étoile explosée qui brille dans le ciel nocturne. Sa réputation grandissante lui valu le patronage du roi danois Frédéric II et, à l’âge de 30 ans, Brahe pu fonder un bel observatoire astronomique sur l’île de Hven, dans la mer du Nord (figure 3.2). Brahe était le dernier et le plus grand des observateurs prétélescopiques en Europe.

À Hven, Brahe enregistra en permanence les positions du Soleil, de la Lune et des planètes pendant près de 20 ans. Ses observations approfondies et précises lui ont permis de constater que les positions des planètes variaient par rapport à celles données dans les tableaux publiés, qui étaient basés sur les travaux de Ptolémée. Ces données étaient extrêmement précieuses, mais Brahe n’avait pas la capacité de les analyser et de développer un meilleur modèle que celui que Ptolémée avait publié. Il était d’autant plus inhibé par son caractère extravagant et acariâtre, et il accumula les ennemis parmi les fonctionnaires du gouvernement.

Lorsque son mécène, Frédéric II, meurt en 1597, Brahe perdit sa base politique et décida de quitter le Danemark. Il s’installa à Prague, où il devient l’astronome de la cour de l’empereur Rodolphe de Bohême. C’est là, l’année précédant sa mort, que Brahe trouva un jeune mathématicien très compétent, Johannes Kepler, pour l’aider à analyser ses nombreuses données planétaires.

Johannes Kepler est né dans une famille pauvre de la province allemande du Wurtemberg et a vécu une grande partie de sa vie dans la tourmente de la guerre de Trente Ans (voir figure 3.2). Il fréquente l’université de Tubingen et se destine à une carrière de théologien. Il y apprend les principes du système copernicien et se convertit à l’hypothèse héliocentrique. Finalement, Kepler se rend à Prague pour servir d’assistant à Brahe, qui le met au travail pour essayer de trouver une théorie satisfaisante du mouvement planétaire, compatible avec la longue série d’observations faites à Hven. Brahe hésite à fournir à Kepler beaucoup de matériel à un moment donné, de peur que ce dernier ne découvre lui-même les secrets du mouvement universel, privant ainsi Brahe d’une partie de la gloire. Ce n’est qu’après la mort de Brahe en 1601 que Kepler entre en pleine possession de ces documents inestimables. Leur étude occupe la majeure partie du temps de Kepler pendant plus de 20 ans.

Grâce à son analyse du mouvement des planètes, Kepler élabore une série de principes, aujourd’hui connus sous le nom des trois lois de Kepler, qui décrivent le comportement des planètes en fonction de leur trajectoire dans l’espace. Les deux premières lois du mouvement des planètes ont été publiées en 1609 dans Astronomia Nova. Leur découverte a constitué une étape importante dans le développement de la science moderne.

La trajectoire d’un objet dans l’espace est appelée son orbite. Kepler a d’abord supposé que les orbites des planètes étaient des cercles, mais cela ne lui a pas permis de trouver des orbites qui correspondaient aux observations de Brahe. En travaillant avec les données relatives à Mars, il a fini par découvrir que l’orbite de cette planète avait la forme d’un cercle quelque peu aplati, ou ellipse. Après le cercle, l’ellipse est la plus simple des courbes fermés, appartenant à une famille de courbes connues sous le nom de sections coniques (figure 3.3).

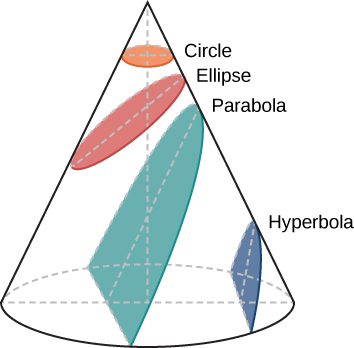
Vous vous souvenez peut-être de vos cours de mathématiques. Dans un cercle, le centre est un point particulier. La distance entre le centre et n’importe quel point du cercle est exactement la même. Dans une ellipse, la somme des distances entre deux points particuliers à l’intérieur de l’ellipse et n’importe quel point de l’ellipse est toujours la même. Ces deux points à l’intérieur de l’ellipse sont appelés ses foyers, un mot inventé à cet effet par Kepler.

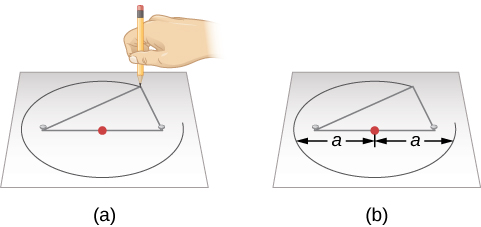
Cette propriété suggère une façon simple de dessiner une ellipse (figure 3.4). Nous enroulons les extrémités d’une boucle de ficelle autour de deux punaises enfoncées dans une feuille de papier sur une planche à dessin, de sorte que la ficelle soit détendue. Si nous poussons un crayon contre la ficelle, ce qui la rend tendue, et que nous faisons ensuite glisser le crayon contre la ficelle tout autour des punaises, la courbe qui en résulte est une ellipse. En tout point où se trouve le crayon, la somme des distances entre le crayon et les deux punaises est une longueur constante - la longueur de la corde. Les punaises se trouvent aux deux foyers de l’ellipse.

Le diamètre le plus large de l’ellipse est appelé son grand axe. La moitié de cette distance, c’est-à-dire la distance entre le centre de l’ellipse et l’une de ses extrémités, constitue le demi-grand axe, qui est généralement utilisé pour préciser la taille de l’ellipse. Par exemple, le demi-grand axe de l’orbite de Mars, qui correspond également à la distance moyenne de la planète par rapport au Soleil, est de 228 millions de kilomètres.

La forme (rondeur) d’une ellipse dépend de la proximité des deux foyers par rapport au grand axe. Le rapport entre la distance entre les foyers et la longueur du grand axe est appelé excentricité de l’ellipse.

Si les foyers (ou les points d’attache) sont déplacés au même endroit, la distance entre les foyers sera nulle. Cela signifie que l’excentricité est nulle et que l’ellipse n’est qu’un cercle ; on peut donc appeler un cercle une ellipse d’excentricité nulle. Dans un cercle, le demi-grand axe serait le rayon.

Ensuite, nous pouvons réaliser des ellipses de différentes élongations (ou longueurs étendues) en variant l’espacement des punaises (tant qu’elles ne sont pas plus éloignées que la longueur de la corde). Plus l’excentricité est grande, plus l’ellipse est allongée, jusqu’à une excentricité maximale de 1,0, lorsque l’ellipse devient "plate", c’est-à-dire à l’opposé d’un cercle.

La taille et la forme d’une ellipse sont entièrement spécifiées par son demi-grand axe et son excentricité. En utilisant les données de Brahe, Kepler a découvert que Mars a une orbite elliptique, avec le Soleil à un foyer (l’autre foyer est vide). L’excentricité de l’orbite de Mars n’est que d’environ 0,1 ; son orbite, dessinée à l’échelle, serait pratiquement indiscernable d’un cercle, mais la différence s’est avérée cruciale pour comprendre les mouvements planétaires.

Kepler a généralisé ce résultat dans sa première loi et a affirmé que les orbites de toutes les planètes sont des ellipses. C’était un moment décisif dans l’histoire de la pensée humaine : il n’était pas nécessaire de n’avoir que des cercles pour avoir un cosmos acceptable. L’univers pouvait être un peu plus complexe que ce que les philosophes grecs avaient voulu.

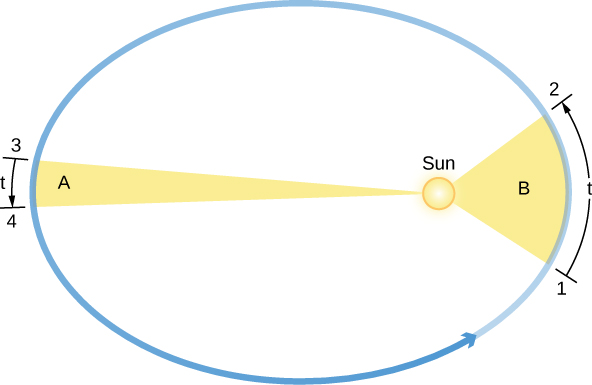
La deuxième loi de Kepler concerne la vitesse à laquelle chaque planète se déplace le long de son ellipse, également appelée vitesse orbitale. En se basant sur les observations de Mars par Brahe, Kepler découvre que la planète accélère lorsqu’elle se rapproche du Soleil et ralentit lorsqu’elle s’en éloigne. Il a exprimé la forme précise de cette relation en imaginant que le Soleil et Mars sont reliés par une ligne droite et élastique. Lorsque Mars est plus proche du Soleil (positions 1 et 2 de la figure 3.5), la ligne élastique n’est pas autant étirée, et la planète se déplace rapidement. Plus loin du Soleil, comme dans les positions 3 et 4, la ligne est beaucoup étirée, et la planète ne se déplace pas aussi rapidement. Lorsque Mars se déplace sur son orbite elliptique autour du Soleil, la ligne élastique balaie des zones de l’ellipse au fur et à mesure de son déplacement (les régions colorées de notre figure). Kepler a découvert qu’à intervalles de temps égaux (t), les zones balayées dans l’espace par cette ligne imaginaire sont toujours égales ; c’est-à-dire que l’aire de la région B de 1 à 2 est la même que celle de la région A de 3 à 4.

Si une planète se déplace sur une orbite circulaire, la ligne élastique est toujours étirée de la même façon et la planète se déplace à une vitesse constante autour de son orbite. Mais, comme Kepler l’a découvert, dans la plupart des orbites, la vitesse d’une planète en orbite autour de son étoile (ou d’une lune en orbite autour de sa planète) a tendance à varier parce que l’orbite est elliptique.

Les deux premières lois du mouvement planétaire de Kepler décrivent la forme de l’orbite d’une planète et permettent de calculer la vitesse de son mouvement en tout point de l’orbite. Kepler est heureux d’avoir découvert ces règles fondamentales, mais elles ne satisfont pas sa quête d’une compréhension complète du mouvement des planètes. Il voulait savoir pourquoi les orbites des planètes étaient espacées comme elles le sont et trouver un modèle mathématique dans leurs mouvements - une "harmonie des sphères" comme il l’appelait. Pendant de nombreuses années, il a travaillé à la découverte de relations mathématiques régissant l’espacement des planètes et le temps que chaque planète mettait à faire le tour du Soleil.

En 1619, Kepler a découvert une relation de base permettant de relier les orbites des planètes à leurs distances relatives par rapport au Soleil. Nous définissons la période orbitale d’une planète ($P$), comme le temps qu’il faut à une planète pour faire une fois le tour du Soleil. Rappelons également que le demi-grand axe d’une planète, $a$, est égal à sa distance moyenne du Soleil. Cette relation, connue aujourd’hui sous le nom de troisième loi de Kepler, indique que la période orbitale d’une planète au carré est proportionnelle au cube du demi-grand axe de son orbite, soit

$P^2\alpha\ a^3$

Lorsque $P$ (la période orbitale) est mesurée en années et que $a$ est exprimé en une quantité appelée unité astronomique (UA), les deux côtés de la formule ne sont pas seulement proportionnels mais égaux. Une UA est la distance moyenne entre la Terre et le Soleil et est approximativement égale à $1,5 × 10^8$ kilomètres. Dans ces unités,

$P^2 = a^3$

La troisième loi de Kepler s’applique à tous les objets en orbite autour du Soleil, y compris la Terre, et fournit un moyen de calculer leurs distances relatives par rapport au Soleil à partir du temps qu’ils mettent à orbiter. Prenons un exemple spécifique pour illustrer l’utilité de la troisième loi de Kepler.

Par exemple, supposons que vous calculez le temps que met Mars à faire le tour du Soleil (en années terrestres). La troisième loi de Kepler peut alors être utilisée pour calculer la distance moyenne de Mars par rapport au Soleil. La période orbitale de Mars (1,88 année terrestre) au carré, ou $P^2$ , est de $1,88^2 = 3,53$, et selon l’équation de la troisième loi de Kepler, elle est égale au cube de son demi-grand axe, ou $a^3$ . Quel nombre doit-on donc cuber pour obtenir 3,53 ? La réponse est 1,52 (puisque $1,52 × 1,52 × 1,52 = 3,53$). Ainsi, le demi-grand axe de Mars, en unités astronomiques, doit être de 1,52 UA. En d’autres termes, pour faire le tour du Soleil en un peu moins de deux ans, Mars doit être éloignée d’environ 50 % de plus du Soleil que ne l’est la Terre.

Les trois lois de Kepler sur le mouvement des planètes peuvent être résumées comme suit :

• Première loi de Kepler : Chaque planète se déplace autour du Soleil sur une orbite qui est une ellipse, avec le Soleil à un foyer de l’ellipse.
• Deuxième loi de Kepler : La ligne droite reliant une planète et le Soleil balaie des surfaces égales dans l’espace à des intervalles de temps égaux.
• La troisième loi de Kepler : Le carré de la période orbitale d’une planète est directement proportionnel au cube du demi-grand axe de son orbite.

Les trois lois de Kepler fournissent une description géométrique précise du mouvement des planètes dans le cadre du système copernicien. Grâce à ces outils, il a été possible de calculer les positions planétaires avec une précision grandement améliorée. Cependant, les lois de Kepler sont purement descriptives : elles ne nous aident pas à comprendre quelles forces de la nature contraignent les planètes à suivre cet ensemble particulier de règles. Cette étape a été laissée à Isaac Newton.