A la fin de cette section, vous serez capable de :
- Décrire les trois lois du mouvement de Newton
- Expliquer comment les trois lois du mouvement de Newton sont liées à la quantité de mouvement
- Définir la masse, le volume et la densité et leur différence
- Définir la quantité de mouvement angulaire
C’est le génie d’Isaac Newton qui a trouvé un cadre conceptuel expliquant complètement les observations et les règles rassemblées par Galilée, Brahe, Kepler et d’autres. Newton est né dans le Lincolnshire, en Angleterre, l’année suivant la mort de Galilée (figure 3.6). Contre l’avis de sa mère, qui souhaitait qu’il reste à la maison pour aider à la ferme familiale, il entre au Trinity College de Cambridge en 1661 et huit ans plus tard, il est nommé professeur de mathématiques. Parmi les contemporains de Newton en Angleterre figurent l’architecte Christopher Wren, les auteurs Aphra Behn et Daniel Defoe, et le compositeur G. F. Haendel.

- Les lois du mouvement de Newton
- Interprétation des lois de Newton
- Masse, volume et densité
- Moment cinétique
Les lois du mouvement de Newton
Jeune homme à l’université, Newton s’est intéressé à la philosophie naturelle, comme on appelait alors la science. Il a élaboré certaines de ses premières idées sur les machines et l’optique pendant les années de peste de 1665 et 1666, lorsque les étudiants ont été renvoyés de l’université. Newton, un homme lunatique et souvent difficile, a continué à travailler sur ses idées en privé, inventant même de nouveaux outils mathématiques pour l’aider à faire face aux complexités impliquées. Finalement, son ami Edmund Halley (présenté dans Comets and Asteroids: Debris of the Solar System) l’a convaincu de rassembler et de publier les résultats de ses remarquables recherches sur le mouvement et la gravité. Le résultat fut un volume qui exposait le système sous-jacent du monde physique, Philosophiae Naturalis Principia Mathematica. Les Principia, comme le livre est généralement connu, ont été publiés aux frais de Halley en 1687.
Au tout début des Principia, Newton propose trois lois qui régiraient les mouvements de tous les objets :
- Première loi de Newton : Chaque objet continuera à être dans un état de repos ou à se déplacer à une vitesse constante en ligne droite à moins qu’il ne soit contraint de changer par une force extérieure.
- Deuxième loi de Newton : Le changement de mouvement d’un corps est proportionnel à et dans la direction de la force qui agit sur lui.
- Troisième loi de Newton : Pour chaque action, il y a une réaction égale et opposée (ou : les actions mutuelles de deux corps l’un sur l’autre sont toujours égales et agissent dans des directions opposées).
Dans le latin original, les trois lois ne contiennent que 59 mots, mais ces quelques mots préparent le terrain pour la science moderne. Examinons-les plus attentivement.
Interprétation des lois de Newton
La première loi de Newton est une reformulation de l’une des découvertes de Galilée, appelée la conservation de la quantité de mouvement. La loi affirme qu’en l’absence de toute influence extérieure, il existe une mesure du mouvement d’un corps, appelée sa quantité de mouvement, qui reste inchangée.
La première loi de Newton est parfois appelée loi d’inertie, où l’inertie est la tendance des objets à continuer à faire ce qu’ils font déjà. En d’autres termes, un objet stationnaire reste en place et un objet en mouvement continue de bouger à moins qu’une force n’intervienne.
Définissons la signification précise de la quantité de mouvement - cela dépend de trois facteurs :
- la vitesse - la vitesse à laquelle un corps se déplace (zéro s’il est immobile),
- la direction de son mouvement
- la masse - une mesure de la quantité de matière dans un corps, dont nous parlerons plus tard.
Les scientifiques utilisent le terme vélocité pour décrire la vitesse et la direction du mouvement. Par exemple, 20 kilomètres à l’heure plein sud est la vélocité, alors que 20 kilomètres à l’heure est la vitesse. La quantité de mouvement peut alors être définie comme la masse d’un objet multipliée par sa vélocité.
Il n’est pas si facile de voir cette règle en action dans le monde de tous les jours en raison des nombreuses forces agissant sur un corps à un moment donné. Une force importante est la friction, qui ralentit généralement les choses. Si vous faites rouler une balle sur le trottoir, elle finit par s’arrêter car le trottoir exerce une force de frottement sur la balle. Mais dans l’espace entre les étoiles, où il y a si peu de matière que les frottements sont insignifiants, les objets peuvent en fait continuer à se déplacer (à dériver) indéfiniment.
La quantité de mouvement d’un corps ne peut changer que sous l’action d’une influence extérieure. La deuxième loi de Newton exprime la force en termes de sa capacité à changer la quantité de mouvement avec le temps. Une force (une poussée ou une traction) a à la fois une intensité et une direction. Lorsqu’une force est appliquée à un corps, la quantité de mouvement change dans la direction de la force appliquée. Cela signifie qu’une force est nécessaire pour modifier la vitesse ou la direction d’un corps, ou les deux, c’est-à-dire pour le mettre en mouvement, l’accélérer, le ralentir, l’arrêter ou changer sa direction.
Comme vous l’avez appris dans Observer le ciel : la naissance de l’astronomie, le taux de variation de la vitesse d’un objet est appelé accélération. Newton a montré que l’accélération d’un corps était proportionnelle à la force qui lui était appliquée. Supposons qu’après une longue période de lecture, vous poussiez un livre d’astronomie loin de vous sur une longue table lisse (nous utilisons une table lisse pour qu’il n’y ai pas de frottements). Si vous poussez le livre régulièrement, il continuera à accélérer tant que vous le pousserez. Plus vous poussez le livre fort, plus son accélération sera importante. Le degré d’accélération d’un objet par une force est également déterminé par la masse de l’objet. Si vous continuiez à pousser un stylo avec la même force avec laquelle vous poussiez le livre, le stylo - ayant moins de masse - serait accéléré à une plus grande vitesse.
La troisième loi de Newton est peut-être la plus profonde des règles qu’il a découvertes. Fondamentalement, c’est une généralisation de la première loi, mais cela nous donne aussi un moyen de définir la masse. Si nous considérons un système de deux ou plusieurs objets isolés des influences extérieures, la première loi de Newton dit que la quantité de mouvement totale des objets doit rester constante. Par conséquent, tout changement de quantité de mouvement au sein du système doit être équilibré par un autre changement égal et opposé afin que la quantité de mouvement de l’ensemble du système ne soit pas modifiée.
Cela signifie que les forces dans la nature ne se produisent pas seules : nous constatons que dans chaque situation, il y a toujours une paire de forces qui sont égales et opposées l’une à l’autre. Si une force est exercée sur un objet, elle doit être exercée par quelque chose d’autre, et l’objet exercera une force égale et opposée sur ce quelque chose. Nous pouvons regarder un exemple simple pour le démontrer.
Supposons qu’un étudiant en astronomie casse-cou - et un skateur passionné - veuille sauter de la fenêtre de son dortoir du deuxième étage sur sa planche (nous ne recommandons pas d’essayer cela !). La force qui le tire vers le bas après avoir sauté (comme nous le verrons dans la section suivante) est la force de gravité entre lui et la Terre. Lui et la Terre doivent tous deux subir le même changement total de quantité de mouvement en raison de l’influence de ces forces mutuelles. Ainsi, l’étudiant et la Terre sont accélérés par l’attraction de l’autre. Cependant, l’étudiant fait beaucoup plus de mouvement. Parce que la Terre a une masse énormément plus grande, elle peut subir le même changement de quantité de mouvement en n’accélérant que d’une très petite quantité. Les choses tombent tout le temps vers la Terre, mais l’accélération de notre planète en conséquence est bien trop faible pour être mesurée.
Un exemple plus évident de la nature mutuelle des forces entre les objets est familier à tous ceux qui jouent au tennis. Le recul que vous ressentez lorsque vous frappez avec votre raquette montre que la balle exerce une force sur elle lors de l’impact, tout comme la raquette sur la balle. De même, lorsque vous tirez avec un fusil, la force poussant la balle hors du canon est égale à la force poussant vers l’arrière sur le fusil et sur votre épaule.
C’est le principe des moteurs à réaction et des fusées : la force qui évacue les gaz d’échappement par l’arrière de la fusée s’accompagne de la force qui pousse la fusée vers l’avant. Les gaz d’échappement n’ont pas besoin de pousser contre l’air ou la Terre ; une fusée fonctionne en fait mieux dans le vide (Figure 3.7).

Pour en savoir plus sur la vie et l’œuvre d’Isaac Newton, consultez cette page chronologique (en anglais) avec des instantanés de sa carrière, produite par la British Broadcasting Corporation (BBC).
Masse, volume et densité
Avant de continuer à discuter des autres travaux de Newton, nous voulons jeter un bref coup d’œil à certains termes qu’il sera important de définir clairement. Nous commençons par la masse, qui est une mesure de la quantité de matière dans un objet.
Le volume d’un objet est la mesure de l’espace physique qu’il occupe. Le volume est mesuré en unités cubiques, telles que les centimètres cubes ou les litres. Le volume est la "taille" d’un objet. Un pièce de monnaie et un ballon gonflé peuvent tous deux avoir la même masse, mais ils ont des volumes très différents. La raison à cela est qu’ils ont également des masses volumiques très différentes, qui est la mesure de la quantité de masse par unité de volume. Plus précisément, la masse volumique est la masse divisée par le volume. Notez que dans le langage courant, nous utilisons souvent «lourd» et «léger» comme indications de masse volumique (plutôt que de poids) comme, par exemple, lorsque nous disons que le fer est lourd ou que la crème fouettée est légère.
Les unités de masse volumique qui seront utilisées dans ce livre sont les grammes par centimètre cube (g/cm3)1. Si un bloc d’un matériau a une masse de 300 grammes et un volume de 100 cm3, sa masse volumique est de 3 g/cm3. Les matériaux familiers couvrent une gamme considérable de densité, des matériaux artificiels tels que la mousse isolante (moins de 0,1 g/cm3) à l’or (19,3 g/cm3). Le tableau 3.1 donne les masses volumiques de certains matériaux familiers. Dans l’univers astronomique, on trouve des masses volumiques bien plus remarquables, depuis la queue d’une comète (10 16 g/cm3) jusqu’à un « cadavre d’étoile » effondré appelé étoile à neutrons (10 15 g/cm3).
| Matériau | masse volumique (g/cm³) |
|---|---|
| or | 19,3 |
| plomb | 11,3 |
| fer | 7,9 |
| terre (en vrac) | 5,5 |
| roche (typique) | 2,5 |
| eau | 1 |
| bois (typique) | 0,8 |
| mousse isolante | 2,5 |
| silicagel | 0,02 |
Tableau 3.1 : masse volumique de matériaux courants
Pour résumer, la masse correspond à la quantité, le volume à la taille et la masse volumique à la densité.
Vous pouvez jouer avec une animation simple démontrant la relation entre les concepts de densité, de masse et de volume, et découvrir pourquoi des objets comme le bois flottent dans l’eau.
- Généralement, nous utilisons des unités métriques standard (ou SI) dans ce livre. L’unité métrique appropriée de densité dans ce système est le kg/m³. Mais pour la plupart des gens, g/cm³ fournit une unité plus significative car la densité de l’eau est exactement de 1 g/cm³, et c’est une information utile pour la comparaison.↩
Moment cinétique
Un concept un peu plus complexe, mais important pour comprendre de nombreux objets astronomiques, est le moment cinétique, qui est une mesure de la rotation d’un corps lorsqu’il tourne autour d’un point fixe (par exemple, une planète en orbite autour du Soleil). Le moment cinétique d’un objet est défini comme le produit de sa masse, de sa vitesse et de sa distance au point fixe autour duquel il tourne.
Si ces trois quantités restent constantes - c’est-à-dire si le mouvement d’un objet particulier a lieu à une vitesse constante à une distance fixe du centre de rotation - alors le moment cinétique est également une constante. La deuxième loi de Kepler est une conséquence de la conservation du moment cinétique. Lorsqu’une planète s’approche du Soleil sur son orbite elliptique et que la distance au centre de rotation diminue, la planète accélère pour conserver le moment cinétique. De même, lorsque la planète est plus éloignée du Soleil, elle se déplace plus lentement.
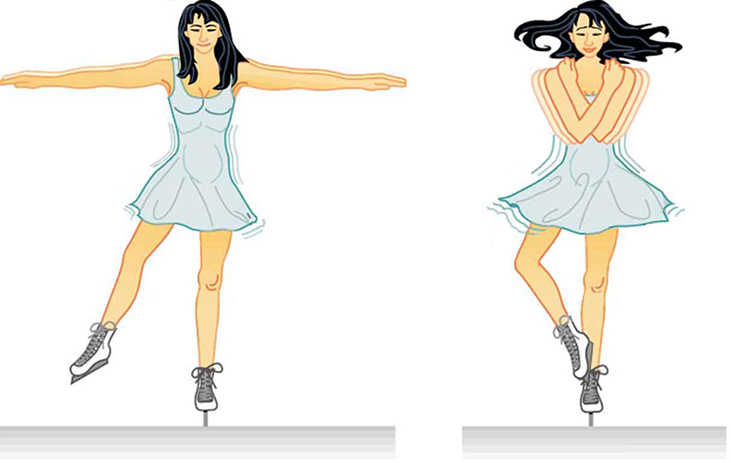
La conservation du moment cinétique est illustrée par les patineurs artistiques, qui rentrent les bras et les jambes pour tourner plus rapidement, et étendent les bras et les jambes pour ralentir (figure 3.8). Vous pouvez le reproduire vous-même sur un tabouret pivotant bien huilé en commençant à tourner lentement avec les bras tendus, puis en tirant les bras vers l’intérieur. Un autre exemple de conservation du moment cinétique est un nuage de poussière qui rétrécit ou une étoile qui s’effondre sur elle-même (les deux sont des situations que vous découvrirez au fur et à mesure de votre lecture). Au fur et à mesure que le matériau se déplace à une distance moindre du centre de rotation, la vitesse du matériau augmente pour conserver le moment cinétique.