Derrière ce nom rallongé se cache en réalité un domaine que vous utilisez régulièrement. La statistique descriptive à une dimension consiste à étudier des données basées sur une seule observation et d’en émettre des conclusions : les notes obtenues par des étudiants, les tailles d’un groupe de personnes ou encore les températures relevées chaque jour pendant une période. Ici, on parle d’une dimension puisque l’on observe qu’une variable, qu’un aspect à la fois. On ne s’intéresse pas à savoir s’il existe un quelconque lien entre deux phénomènes, on ne regarde qu’une chose à la fois : c’est le rôle de la statistique descriptive à une dimension (ou statistique unidimensionnelle).
L’objectif de ce tutoriel est double : vous exposer tout le vocabulaire nécessaire aux études statistiques, et vous introduire les différentes notions de mesures statistiques pour exploiter des données unidimensionnelles. Vous serez alors le roi des statistiques (à une dimension toujours  ).
).
Bien que vous n’ayez pas besoin de grandes connaissances en mathématiques, il est néanmoins utile d’avoir quelques bases pour appréhender correctement ce tutoriel. En particulier, comprendre l’indice de sommation $\Sigma$ est indispensable. Certains points demandent quelques connaissances avancées, mais l’objectif global du tutoriel est qu’un étudiant en fin de lycée ou début de cycle universitaire puisse découvrir cette discipline sans grandes difficultés.
Je remercie tout particulièrement Looping, Anto59290, KFC et Holosmos pour m’avoir donné plusieurs conseils afin d’aboutir à ce tutoriel.
- Vocabulaire
- Les types de variable
- Mesure de tendance centrale
- Mesure de dispersion
- Mesure de forme
- Mesure de concentration
- Représentations graphiques
- Exercice d'application
Vocabulaire
Avant de se lancer directement dans l’exploitation des résultats, nous devons fixer quelques mots de vocabulaire. En effet, nous allons avoir beaucoup d’informations et plusieurs types de variables. Il est donc nécessaire de bien formaliser tout ceci au début. Cette partie est assez dense, mais elle a le mérite de poser les bases et de lever toute ambiguïté quant à la nature des mots employés  . Commençons par l’environnement d’une étude statistique, les Qui ? Quoi ? indispensables à chaque étude statistique.
. Commençons par l’environnement d’une étude statistique, les Qui ? Quoi ? indispensables à chaque étude statistique.
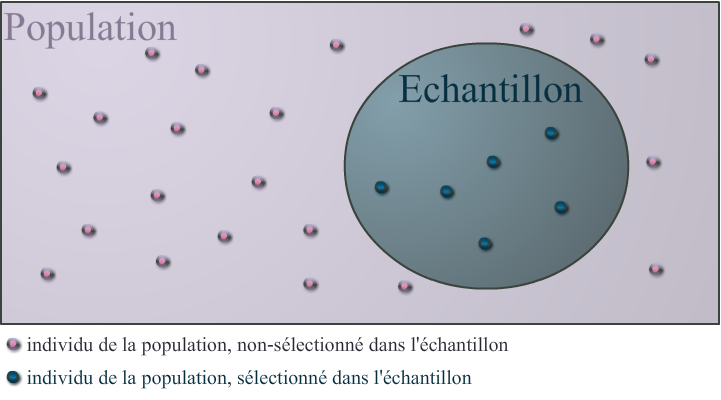
- L’individu est l’unité d’observation. Par exemple, dans un sondage, un individu est une personne ayant répondu au sondage. Mais cela peut aussi être un objet, comme par exemple un comparatif de performance entre plusieurs voitures.
- La population est l’ensemble des individus concernés par l’étude. L’ensemble des entreprises françaises est une population.
- L’échantillon est la partie de la population que l’on étudie. L’ensemble de $1000$ entreprises françaises tirées au hasard constitue un échantillon de la population précédente.
Il ne faut absolument pas confondre échantillon et population ! En statistique descriptive, on décrit un échantillon et non une population ! Ce dernier cas est le rôle de la statistique inférentielle dont le but est d’estimer les caractéristiques d’une population à partir d’un échantillon.
Si j’insiste sur ce point, c’est que l’on a souvent tendance à tirer des conclusions trop hâtives lorsque l’on étudie un échantillon sans en considérer la nature. Comme vous pouvez le remarquer, pour effectuer des études statistiques, il ne suffit pas de savoir faire des calculs, il faut également avoir des connaissances dans le domaine de l’étude !
Pour vous aider, voici un schéma réalisé par Blackline qui résume très bien ce qui a été dit plus haut
À présent, nous allons définir les variables, car c’est ce qui nous intéresse tout particulièrement. Une variable est une caractéristique (un "aspect") d’un individu. Par exemple, la taille d’une personne, la température de l’air à une date donnée ou la vitesse maximale d’une voiture sont des variables. Le principe d’une variable peut se comprendre à l’aide du schéma suivant.

En résumé, une population est constituée d’individus. Tous ces individus possèdent leurs propres caractéristiques (pour des personnes, cela correspond à la taille, l’âge, le nom, …), que l’on regroupe sous forme de variables. Seulement, dans une étude statistique, on ne s’intéresse qu’à une partie de cette population, et cette partie est appelée l’échantillon.
Un premier exemple
On souhaite réaliser un sondage à Paris pour connaître le temps de trajet moyen des utilisateurs des transports en commun pour aller travailler. Pour cela, à chaque personne sondée, on recueille :
- Son âge et sa catégorie socio-professionnelle (CSP)
- Son temps moyen passé dans les transports en commun
On a donc trois variables (l’âge, la CSP et le temps moyen). Essayons de définir correctement l’environnement de l’étude :
- Ici, les individus sont les personnes sondées.
- La population est l’ensemble des personnes utilisant les transports en commun.
- L’échantillon est l’ensemble des personnes ayant répondu favorablement au sondage. Lorsque l’on connait l’endroit et l’heure du sondage, il est utile de le préciser.
Une fois que tout ceci est fixé, nous pouvons commencer à travailler avec nos données. Cela permet notamment de bien fixer les idées quant au sujet de l’étude.
Notez qu’en règle général, en statistique descriptive, le choix de la population peut différer pour un même échantillon mais sous une autre étude. En revanche, ici, il est nécessaire de bien définir notre échantillon, car c’est sur cet échantillon que nous allons travailler et émettre des conclusions après l’étude.
Les types de variable
Il existe deux types de variables, les unes à valeurs numériques, et les autres à valeurs ordinales.
- Les variables quantitatives, qui sont des variables à valeurs numériques, pour lesquelles les opérations arithmétiques ont un sens. Par exemple, un âge, une distance, un volume, etc.
- Les variables qualitatives, où les valeurs possibles sont codées par des modalités (ou catégories). Par exemple, la couleur des yeux, le département, ou tout autre codage où les opérations arithmétiques ne sont pas correctement définies.
Parmi les variables quantitatives, on dispose des variables discrètes et continues. Enfin, parmi les variables qualitatives, on retrouve les variables nominales et ordinales. Nous allons présenter en détail les variables quantitatives plus bas. Pour les variables discrètes, la différence réside dans le fait qu’une variable ordinale est naturellement ordonnée (mention au Baccalauréat, niveau d’appréciation d’un produit, …) alors qu’une variable nominale ne dispose d’aucun ordre (on ne peut pas ranger dans un ordre précis la couleur des yeux, ou la localisation d’une entreprise).
Un moyen de faire la différence entre ces deux types est de remarquer que quantitatif se rapproche de quantité, c’est-à-dire numérique.
Dans le cadre de ce tutoriel, nous n’étudierons que le cas des variables quantitatives. Lorsque l’on étudie une variable qualitative, il y a plusieurs paramètres à prendre en compte, ce qui rend leur manipulation plus délicate.
Il est conseillé de faire des pauses et de lire cette partie plusieurs fois : il y a beaucoup de notions, une multitude de notations et des concepts assez différents de ceux que vous avez l’habitude d’utiliser. Il est tout à fait normal de ne pas tout comprendre à la première lecture, allez-y à votre rythme. 
Les variables quantitatives discrètes
Commençons par le cas le plus simple, celui des variables (quantitatives) discrètes. Il s’agit des variables prenant leurs valeurs dans un ensemble fixé dénombrable. Par conséquent, si $X$ est une variable discrète, elle peut prendre $k$ valeurs différentes :
Où les $a_i$ sont des valeurs numériques, avec $i$ un nombre entier entre $1$ et $k$.
Très souvent, j’utiliserai $i$ en tant qu’indice se situant entre $1$ et $k$. Par exemple, $a_i$ est le $i$-ème élément de l’ensemble $\left \{ a_1, ..., a_k \right \}$.
$k$ est donc le nombre d’éléments de l’ensemble précédent. Par exemple, si l’on reprend le premier exemple, la variable âge est à valeurs dans $\{ 1, 2, ... N, ... \}$ (on veillera à prendre $N$ assez grand mais assez réaliste : il est inutile de prendre $N=1000$ par exemple). Pour chaque valeur $a_i$, on note $n_i$ l’effectif, soit le nombre d’individus dont la variable $X$ a pour valeur $a_i$. Usuellement, on omet volontairement les valeurs qui ne sont pas prises au moins une fois par un individu. Par exemple, j’observe l’âge de $10$ personnes, ce qui me donne la séquence suivante :
On considère alors que les valeurs que peut prendre la variable âge sont $\{22,26,31,45\}$.
Ce qu’il faut bien comprendre, c’est que les valeurs que peut prendre une variable sont uniquement en rapport avec l’échantillon ! En effet, ici, nous avons listé toutes les valeurs présentes dans l’échantillon, mais nous sommes bien d’accord que l’on peut avoir $19$ ou $52$ ans.
Mais si l’on se trompe et que l’on rajoute une valeur en plus, est-ce que cela change tout ?
Dans une étude statistique, cela signifie que l’on ajoute du "bruit", soit des informations non utiles ou non désirées. Par exemple, dans ma séquence d’âges, inscrire $60$ ne serait pas utile puisque aucune des $10$ personnes n’a $60$ ans. C’est pour cette raison que l’on ne se focalise que sur les valeurs observées, sans rajouter d’autres informations. À présent, précisons quelques données élémentaires sur les variables. Pour mieux les comprendre, nous allons rester sur l’exemple précédent des 10 personnes (pour rappel $22,45,22,26,26,31,45,31,31,45$) :
- L’effectif, associé à la valeur $a_i$, et noté $n_i$, est le nombre d’individus dont la variable $X$ vaut $a_i$. Par exemple, l’effectif associé à $22$ est $2$ puisqu’il y a deux individus ayant $22$ ans.
- L’effectif total est le nombre d’individus (ici, il s’agit de $n$). Ici, il y en a $10$.
- La fréquence (associée à une valeur) est le rapport de l’effectif sur l’effectif total. On note $f$ la fréquence et elle est définie, pour la $i$-ème valeur $a_i$ :
La fréquence pour $22$ est donc $\frac{2}{10}=0,2$.
- La fréquence cumulée (ascendante) est la somme des fréquences du début jusqu’à la valeur concernée. On note $F$ la fréquence cumulée et elle est définie, pour la $i$-ème valeur prise par $X$ :
La fréquence cumulée pour $22$ est donc $0,2$, puisque $22$ est la première valeur ordonnée de cette série.
Voici un petit récapitulatif des symboles et lettres que nous utiliserons systématiquement par la suite :
| Nombre de valeurs possibles | Valeur possible | Effectif | Fréquence | Fréquence cumulée |
|---|---|---|---|---|
| $k$ | $a_i$ | $n_i$ | $f_i$ | $F_i$ |
Remarquons ces propriétés immédiates :
Exercice
Pour vous entraîner, commencez par remplir le tableau correspondant à la séquence :
| $X$ | $n$ | $f$ | $F$ |
|---|---|---|---|
| $22$ | $2$ | $0,2$ | $0,2$ |
| $26$ | $2$ | $0,2$ | $0,4$ |
| $31$ | |||
| $45$ | $1$ |
| $X$ | $n$ | $f$ | $F$ |
|---|---|---|---|
| $22$ | $2$ | $0,2$ | $0,2$ |
| $26$ | $2$ | $0,2$ | $0,4$ |
| $31$ | $3$ | $0,3$ | $0,7$ |
| $45$ | $3$ | $0,3$ | $1$ |
Distribution
En théorie des probabilités, la notion de distribution est très importante et revient fréquemment. C’est également le cas en statistiques. Une distribution est un tableau tel que, pour chaque valeur possible $a_i$, on associe sa fréquence $f_i$.
En théorie des probabilités, on parle plutôt de loi de probabilité (loi discrète, continue, …) alors qu’en statistique, on utilise le terme distribution (théorique, empirique, …).
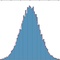
On a ainsi tendance à regrouper les distributions par des fonctions lorsque l’on travaille sur des données théoriques (lois de probabilités) et par des histogrammes (j’expliquerai les histogrammes en détail plus loin) lorsque l’on travaille sur des données concrètes. La distribution d’une loi normale (loi de référence en probabilités et statistiques) est donnée par cette courbe

En particulier, cela signifie que la plupart des observations se situent autour de $\mu$. Je ne rentrerais pas dans les détails sur cette loi, car il me faudrait parler de plusieurs concepts de la théorie des probabilités. L’avantage d’une distribution, c’est que c’est visuellement parlant. En un coup d’œil, cela nous renseigne sur la répartition des différentes valeurs.
Les variables quantitatives continues : le problème d’agrégation
Hormis les variables discrètes, nous rencontrons également un autre type de variable : les variables continues. Lorsque l’on ne connaît pas à l’avance les différentes valeurs que peuvent prendre une variable ou que l’on travaille sur des nombres réels (à virgule), la variable est alors continue. On distingue une particularité sur les variables continues : celles-ci peuvent être agrégées, ce qui change la façon dont nous étudions la variable. Lorsqu’une variable est agrégée, c’est qu’elle a été traitée statistiquement.
Traitée statistiquement ? Qu’est ce que cela veut dire ? 
Il existe des dizaines de procédés de traitement de données. Dans la réalité, on dispose au départ de données dites brutes. Ensuite, en fonction de ce que l’on souhaite en faire, nous allons faire du ménage parmi ces données : supprimer des valeurs aberrantes ou les regrouper par classes. Au final, avec des données agrégées, tout est propre, il n’y a plus qu’à les manipuler  .
.
Dans ce cas, pourquoi est-ce que les variables continues ne sont pas toutes agrégées ?
Et bien deux choses se passent lors de l’agrégation de données :
- Il y a souvent perte de l’information. En effet, à cause du regroupement par classes (que nous allons voir), les valeurs associées aux variables de chaque individu sont rangées "par paquets", et ne sont plus considérés telles quelles.
- Tout dépend du contexte : en fonction de ce que vous souhaitez étudier, vous n’allez pas traiter les données de la même façon.
Les cas agrégé
Dans le cas agrégé, c’est-à-dire où les variables sont rangées par classes, on ordonne d’une manière similaire aux variables discrètes en créant $k$ classes :
Avec $a_1 < a_2 < ... < a_k < a_{k+1}$. Nous allons donc définir les effectifs, fréquences et fréquences cumulées par classes :
| $X$ | $n$ | $f$ | $F$ |
|---|---|---|---|
| $[a_1, a_2[$ | $n_1$ | $f_1$ | $F_1=f_1$ |
| $[a_2, a_3[$ | $n_2$ | $f_2$ | $F_2=f_1+f_2$ |
| $...$ | $...$ | $...$ | $...$ |
| $[a_k, a_{k+1}[$ | $n_k$ | $f_k$ | $1$ |
Dans le cas des variables agrégées, on introduit $c_i$, les milieux des classes où, pour tout $1 \leq i \leq k$ :
Le cas non agrégé
Dans le cas non agrégé, on considère chaque valeur associée aux variables de chaque individu de manière unique : il n’y a plus de regroupement dans des classes. Ainsi, on note $x_1, ... x_n$ les valeurs prises par la variable $X$ pour chaque individu (puisqu’il y a $n$ individus).
Données non agrégées ne veut pas dire mauvaises données ! Il s’agit juste de données non traitées, mais rappelez vous que l’on traite des données dans un but précis. Lorsque l’on ne sait pas dans quel objectif sera utilisé des données, mieux vaut les laisser brutes.
Mesure de tendance centrale
Dans un premier temps, commençons en douceur avec les mesures de tendance centrale. Il s’agit des mesures les plus classiques et celles qui permettent de résumer le plus simplement un échantillon. En particulier, les mesures de tendance centrale permettent d’obtenir des informations "de groupe", c’est-à-dire vers quelles valeurs les variables ont tendance à se concentrer. Définissons une mesure de tendance que vous connaissez tous et que vous utilisez le plus souvent : la moyenne arithmétique !
La moyenne arithmétique
Concrètement, la moyenne (arithmétique) est la mesure permettant de résumer le plus simplement l’échantillon. On la note souvent avec une barre au dessus de la variable.
| Discrète | Continue agrégée | Continue non agrégée |
|---|---|---|
| $\displaystyle \overline{X}=\sum_{i=1}^k f_i a_i$ | $\displaystyle \overline{X}=\sum_{i=1}^k f_i c_i$ | $\displaystyle \overline{X}=\frac{1}{n} \sum_{i=1}^n x_i$ |
Pour rappel, dans le cas continu agrégé, on dispose de $k$ classes dont le milieu de chaque classe est donnée par :
On utilise couramment le terme moyenne pour définir la moyenne arithmétique, mais sachez qu’il existe d’autres moyennes (si vous souhaitez approfondir, je vous laisse vous documenter à ce sujet). Par exemple, pour une variable continue non agrégée, on peut définir plusieurs moyennes :
| Arithmétique | Géométrique | Quadratique | Harmonique | Générale d’ordre $p$ |
|---|---|---|---|---|
| $\displaystyle \overline{X}=\frac{1}{n} \sum_{i=1}^n x_i$ | $\displaystyle G=\left( \prod_{i=1}^n x_i \right)^{\frac{1}{n}}$ | $\displaystyle Q=\sqrt{\frac{1}{n} \sum_{i=1}^n x_i^2}$ | $\displaystyle H=\frac{n}{\sum_{i=1}^n \frac{1}{x_i}}$ | $\displaystyle \mathcal{M}_p=\left(\frac{1}{n} \sum_{i=1}^n x_i^p \right)^{\frac{1}{p}}$ |
Par exemple, on utilise la moyenne géométrique lorsque l’on souhaite calculer une moyenne de taux, ou encore la moyenne harmonique pour déterminer la vitesse moyenne de plusieurs trajets.
Pourquoi définissons-nous la moyenne de cette manière ?
Cette mesure permet de résumer grossièrement un échantillon. Dans l’idée, cela signifie que si j’ajoute un individu dans mon échantillon, celui-ci devrait avoir une valeur proche de la moyenne. Autrement dit, il s’agit de la valeur que tous les individus devraient avoir dans le cas le plus hypothétique possible. Par exemple, dans une classe d’étudiants, si la moyenne pour un examen est de $10$, cela signifie que si tous les étudiants de cette promotion auraient obtenu $10$, la moyenne en serait inchangée.
Mais alors la moyenne peut-être trompeuse ?
Oui ! C’est là un des gros problèmes de la moyenne : en plus d’être sensible aux valeurs extrêmes (c’est-à-dire aux grandes valeurs par rapport aux autres), elle ne mesure pas la dispersion des individus. Par exemple, prenons 2 groupes de 6 étudiants ayant passé le même examen et on donne les notes de chaque groupe :
| Groupe | Notes | Moyenne |
|---|---|---|
| A | $10,10,10,10,10,10$ | $10$ |
| B | $0,0,0,20,20,20$ | $10$ |
Voyez-vous le problème ? Nous avons la même moyenne pour les deux groupes, alors que le premier groupe est complètement homogène, et le second complètement hétérogène. C’est pour cette raison que l’on dit souvent qu’il ne faut pas se fier uniquement à la moyenne car elle est souvent trompeuse. Pour compléter les informations, on utilise ensuite les mesures de dispersions (c’est dans la partie suivante  ) ou encore la médiane, plus fiable que la moyenne, mais aussi plus restrictive.
) ou encore la médiane, plus fiable que la moyenne, mais aussi plus restrictive.
La médiane
Il s’agit de la deuxième mesure que l’on calcule très souvent en statistique. La médiane est la valeur telle qu’il y ait autant d’observations au-dessus qu’en-dessous. Mathématiquement, la médiane est définie comme ceci :
En mathématiques, on cherche souvent à calculer des minimums ou maximums de listes, fonctions ou suites. Par exemple, si $A=\min_{x \in \mathbb{R}} f(x)$ alors $A$ est la plus petite valeur atteinte par $f$ sur $\mathbb{R}$. Maintenant, supposons que je souhaite obtenir non pas la plus petite valeur atteinte par $f$, mais le $x$ qui fait atteindre $f$ à sa plus petite valeur ? C’est là qu’intervient $\text{argmin}$, qui a pour rôle de fournir ce fameux $x$. Pour exemple, les deux équations suivantes sont équivalentes :
Ainsi, la quantité $Med$ est la valeur telle que
Et un bon moyen de connaître le nombre d’observation situées de part et d’autre d’une valeur, c’est de regarder la fréquence cumulée ! En effet, s’il y a autant d’observations au-dessus d’une valeur qu’en-dessous, cela signifie que la fréquence cumulée est égale à $0,5$ au point d’abscisse $Med$. On en déduit que $Med=F^{-1}(0,5)$. Pour bien comprendre l’utilisation de la fonction réciproque, aidez-vous du graphique suivant :
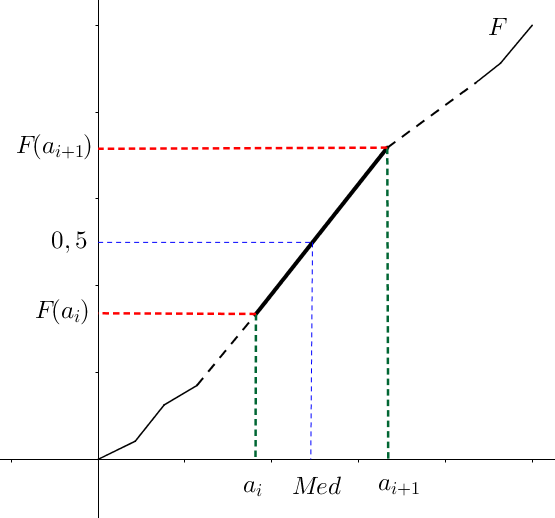
Une des différences par rapport à la moyenne, c’est qu’il n’y a pas de calcul algébrique général ! En effet, en fonction du type de variable, il peut s’agir de "trouver" la valeur, et non de la calculer.
Cas discret
Regardons le tableau suivant :
| $X$ | $F$ |
|---|---|
| $..$ | $..$ |
| $a_i$ | $F_i<0,5$ |
| $a_{i+1}$ | $F_{i+1}>0,5$ |
| $..$ | $..$ |
D’après ce que l’on a dit auparavant, la médiane se situe entre $a_i$ et $a_{i+1}$. Usuellement, on considère alors que, dans ce cas, $Med=a_{i+1}$. En revanche, si j’avais eu $F_i=0,5$ alors on aurait considéré $Med=a_i$.
Le cas continu non agrégé
Pour rappel, non agrégé signifie que l’on dispose de $n$ observations $x_i$ pour la variable $X$. Seulement, on souhaite disposer d’observations rangées dans l’ordre croissant. Pour ce faire, on introduit une bijection $\varphi : \{1, ..., n\} \rightarrow \{1, ..., n\}$ telle que :
Ainsi, on obtient une suite d’observations $(x_{\varphi(i)})$ rangées dans l’ordre croissant. L’intérêt de cette manipulation, c’est que l’on va pouvoir facilement accéder à l’élément "milieu" de cette liste ordonnée, car c’est l’élément le plus au milieu qui nous intéresse pour pouvoir correctement calculer la médiane. Définissons deux cas en fonction de $n$ :
- Si $n$ est impair alors la médiane est la valeur au milieu :
- Si $n$ est pair alors la médiane est la moyenne arithmétique des deux valeurs centrales :
La particularité du cas agrégé
Dans le cas où notre variable est agrégée, la formule est légèrement plus compliquée. En effet, il est rare qu’il existe une fréquence cumulée ayant pour valeur exactement $0,5$. Dans ce cas, nous allons trouver deux fréquences cumulées qui encadrent $0,5$ et effectuer une interpolation linéaire. Supposons que $F(a_i)<0,5$ et $F(a_{i+1}) > 0,5$ (dans le cas où $F(a_i)=0,5, Med$ vaut alors $a_{i+1}$), avec $1 \leq i \leq k$ alors la médiane est :
Démonstration
On cherche à résoudre $Med=F^{-1}(0,5)$. On suppose que $F$ est affine sur l’intervalle $[a_i, a_{i+1}]$. On a donc :
Il reste alors à remplacer $x$ par $0,5$ et on trouve bien la valeur de la médiane. 
Retour sur notre exemple
À présent, je vous propose un exemple (merci à Looping) qui démontre bien l’intérêt de la médiane. Sur une promotion de 20 étudiants, 19 d’entre-eux sont embauchés avec un salaire situé entre $20000$ et $30000$ dollars par an. En revanche, un étudiant est, quant à lui, embauché à un million de dollars par an. Quelle est la moyenne ici ?
L’université en question pourrait alors dire "À la sortie de l’université, nos étudiants ont un salaire moyen de 73750 dollars par an !". Et pourtant, s’agit-il de la réalité ? Si l’on regarde le salaire médian, on s’aperçoit qu’il est entre $20000$ et $30000$ dollars par an ($25000$ dollars par an si l’on prends le milieu des classes). En conclusion, le salaire médian est ici beaucoup plus significatif que le salaire moyen.
Globalement, dès que vous détectez une valeur extrême dans votre échantillon (une valeur bien trop importante par rapport aux autres), méfiez-vous de la moyenne.
Quartiles, déciles et quantiles
Essayons de généraliser la notion de médiane. Par exemple, si maintenant, je souhaite couper non plus en deux mais en quatre ma distribution, de sorte qu’un quart des individus se situent en-dessous d’une certaine valeur, et qu’un quart des individus se situent au-dessus d’une autre valeur (toujours en regardant la fréquence cumulée). Soit $\alpha \in ]0,1[$ alors on note $q_{\alpha}$ le quantile d’ordre $\alpha$, c’est-à-dire que l’on a $\alpha$ % d’observations en dessous de $q_{\alpha}$ et $100-\alpha$ % observations au-dessus de $q_{\alpha}$ :
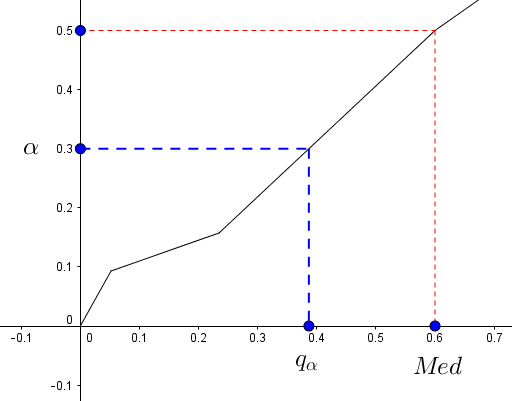
Ici, par exemple, on a pris $\alpha=0,3$, de sorte que $30$ % des individus (au sens de la fréquence cumulée) se situent en-dessous de $q_{\alpha} \approx 0,4$. Dans la suite, on considérera toujours que $0 < \alpha < 1$.
Cas discret
Comme pour la médiane, on regarde au niveau de la fréquence cumulée.
| $X$ | $F$ |
|---|---|
| $..$ | $..$ |
| $a_i$ | $F_i< \alpha$ |
| $a_{i+1}$ | $F_{i+1}>\alpha$ |
| $..$ | $..$ |
D’après ce que l’on a dit auparavant, le quantile $q_{\alpha}$ se situe entre $a_i$ et $a_{i+1}$. On a donc $q_{\alpha}=a_{i+1}$. Si on aurait eu $F_i=\alpha$ alors on aurait considéré $q_{\alpha}=a_i$.
Cas continu non agrégé
On reprend notre bijection $\varphi : \{1, ..., n\} \rightarrow \{1, ..., n\}$. Ici, la tâche est plus délicate et il y a plusieurs manières de définir un quantile d’ordre $\alpha$. On utilisera :
Où $x \mapsto \left \lfloor x \right \rfloor$ est la fonction partie entière. À noter qu’il faut utiliser les quantiles uniquement dans un environnement propice : inutile de déterminer une quantile d’ordre $0,1$ si vous n’avez qu’une vingtaine d’observations.
Toujours ce cas agrégé
C’est exactement le même raisonnement que dans le cas de la médiane, sauf qu’au lieu de s’intéresser à $0,5$, on s’intéresse à $\alpha$. Supposons que $F(a_i)<\alpha$ et $F(a_{i+1}) > \alpha$ (encore une fois, dans le cas où $F(a_i)=\alpha, q_{\alpha}$ vaut alors $a_{i+1}$), avec $1 \leq i \leq k$ alors le quantile d’ordre $\alpha$ est :
La démonstration est la même puisque l’idée consiste encore à effectuer une interpolation linéaire 
Quelques valeurs importantes
En statistique, on utilise très souvent les quantiles pour "partager" un échantillon en plusieurs groupes. Pour cela, les quantiles sont très utiles et on retrouve souvent la notion de quartile ou de décile. On note très souvent $Q1=q_{0,25}$ le premier quartile et $Q3=q_{0,75}$ le troisième quartile (accessoirement, $Q2=Med$) de sorte que l’échantillon soit partagé en quatre groupes. On utilise quelques fois la notion d’écart inter-quartile qui mesure l’écart parmi les $75$ % individus les plus proches de la médiane. Cette mesure est définie par :
On résume dans le tableau ci-dessous quelques valeurs usuelles :
| Nom | Valeurs possibles |
|---|---|
| Quartiles | $\alpha \in \{ 0.25, 0.5, 0.75 \}$ |
| Déciles | $\alpha \in \{ 0.1, 0.2, ..., 0.9 \}$ |
| Centiles | $\alpha \in \{ 0.01, 0.02, ..., 0.99 \}$ |
Mode et classe modale
Le mode est, dans le cas d’une variable discrète ou continu non agrégée, la valeur la plus fréquente (c’est-à-dire la valeur qui est prise le plus grand nombre de fois par les individus). Dans le cas continu agrégée, on n’utilise non pas le mode mais la classe modale (à cause du regroupement par classes) qui est la classe de fréquence la plus élevée.
La classe médiane
Pour une variable continue agrégée, lorsque l’on ne souhaite pas réaliser d’interpolation pour déterminer la médiane (par manque d’informations souvent), on utilise la classe médiane, notée $CMed$ qui est la première classe dont la fréquence cumulée atteint $0,5$. Par exemple, si $F_3=0,4$ et $F_4=0,6$, alors $CMed=[a_4, a_5[$.
De manière générale, la moyenne et les quantiles sont les deux principales mesures nécessaires à l’étude statistique, mais il est toujours utile de garder dans un coin de la tête ces mesures qui peuvent toujours nous aider dans certaines situations.
Mesure de dispersion
Mesurer la dispersion d’un échantillon, c’est quantifier la manière dont les valeurs prises par la variable se comportent entre-elles, selon qu’elle soient proches ou éloignées les unes des autres.
L’étendue
L’étendue est la mesure de dispersion la plus simple. Comme son nom l’indique, cette mesure précise l’écart entre la plus petite et la plus grande valeur, d’où l’étendue de toutes les valeurs. Il s’agit alors simplement d’une différence de deux valeurs, que l’on note $\delta$ :
| Discrète | Continue agrégée | Continue non agrégée |
|---|---|---|
| $\delta=a_k-a_1$ | $\delta=a_{k+1}-a_1$ | $\delta=x_{\varphi(n)}-x_{\varphi(1)}$ |
Où $\varphi$ est toujours cette bijection de $\{1, ..., n\}$ dans $\{1, ..., n\}$ qui ordonne les $(x_i)$ dans l’ordre croissant. Ce calcul s’effectue à vue d’œil : cela nous donne rapidement une idée sur la façon dont les individus se répartissent. Évidemment, cette mesure est très sensible aux valeurs extrêmes.
Revenons au problème de la moyenne. Rappelez-vous, nous avions mis en évidence le problème d’interprétation de la moyenne dans le cas de nos deux groupes de 6 étudiants. L’objectif est donc de construire une mesure permettant de mesurer cette dispersion des individus autour d’une valeur, habituellement la moyenne.
Écart moyen absolu
Créons ensemble cette mesure. Je prends une réalisation $x_i$ d’un individu, et puisque je souhaite mesurer la dispersion autour de la moyenne, le calcul le plus "naturel" pour la mesurer est la distance en valeur absolue, c’est-à-dire $|x_i-\overline{x}|$. Et si l’on somme pour chaque individu, puisque l’on veut étudier la dispersion de l’ensemble des valeurs, on obtient :
Mais je ne veux que cette mesure soit relatif à la taille de l’échantillon, je devrais donc multiplier chaque distance par un poids, ou plutôt considérer que toutes les observations aient autant de chances de se produire (i.e. qui suit une loi uniforme), ce qui me donnerait :
Et c’est ainsi que nous avons crée notre première mesure de dispersion : l’écart moyen absolu !
| Discrète | Continue agrégée | Continue non agrégée |
|---|---|---|
| $\displaystyle EMA= \sum_{i=1}^k f_i\vert a_i-\overline{x}\vert$ | $\displaystyle EMA=\sum_{i=1}^k f_i \vert c_i-\overline{x}\vert $ | $\displaystyle EMA=\frac{1}{n} \sum_{i=1}^n \vert x_i-\overline{x}\vert $ |
Il existe également l’écart médian absolu, où cette fois-ci, on mesure la dispersion autour de la médiane ! Elle se construit de la même manière :
| Discrète | Continue agrégée | Continue non agrégée |
|---|---|---|
| $\displaystyle \sum_{i=1}^k f_i\vert a_i-Med\vert $ | $\displaystyle \sum_{i=1}^k f_i \vert c_i-Med\vert $ | $\displaystyle \frac{1}{n} \sum_{i=1}^n \vert x_i-Med\vert $ |
Seulement, dans les faits, on n’utilise pas souvent l’écart moyen absolu, mais plutôt une autre mesure. Je vous donnerai l’explication après avoir présenté cette autre mesure, ne vous inquiétez pas. 
Variance et écart-type
Intuitivement, la variance mesure la dispersion (quadratique) de la variable autour de sa moyenne. Plus la variance est faible, plus les différentes valeurs prises par les individus sont "proches" de la moyenne. On note $v$ (ou $s^2$) la variance.
| Discrète | Continue agrégée | Continue non agrégée |
|---|---|---|
| $\displaystyle v= \sum_{i=1}^k f_i(a_i-\overline{x})^2$ | $\displaystyle v=\sum_{i=1}^k f_i (c_i-\overline{x})^2$ | $\displaystyle v=\frac{1}{n} \sum_{i=1}^n (x_i-\overline{x})^2$ |
On définit ainsi l’écart-type par : $\sigma=s=\sqrt{v}$. On utilise souvent cette mesure puisque, en plus de se ramener à des plus petites valeurs, elle apparaît dans des calculs de statistique où la variance est très souvent inscrite dans une racine carrée.
Pourquoi utilise-t-on plus souvent la variance, alors qu’elle semble plus compliquée que l’écart moyen absolu ?
Il faut savoir que les mathématiciens adorent les objets "pratiques". En particulier, lorsque l’on travaille avec des fonctions, on aime bien qu’elles soient continues, dérivables voir de classe $C^k$. Et c’est ici l’avantage de la variance : cette dernière est différentiable dans $\mathbb{R}^n$ par somme d’applications différentiables, alors que l’écart moyen absolu ne l’est pas (ou en tout cas, pas en un nombre fini de points) dans $\mathbb{R}^n$ (la dérivée de la valeur absolue n’est pas aussi maniable que celle du polynôme du second degré), ce qui rajoute de la complexité dans les problèmes d’optimisation entre autre (on utilise fréquemment la méthode des moindres carrés ordinaires pour la régression, méthode issue de l’optimisation).
Ainsi, dans toute la suite, on préférera s’intéresser à la variance. Néanmoins, dans certains cas, l’écart moyen absolu peut également se révéler utile, à conserver donc dans un coin de la tête. 
Tout l’intérêt de la variance
Reprenons le tableau des notes des deux groupes d’étudiants :
| Groupe | Notes | Moyenne | Variance | Écart-type |
|---|---|---|---|---|
| A | $10,10,10,10,10,10$ | $10$ | $0$ | $0$ |
| B | $0,0,0,20,20,20$ | $10$ | $100$ | $10$ |
Comme vous pouvez le constater, là où la moyenne ne nous donnait pas plus d’informations, la variance et l’écart-type nous donnent toutes les informations pour comprendre la situation. En effet, le premier groupe est bien homogène car sa variance est nulle alors que le second est très hétérogène puisque sa variance est de $100$.
Retenez qu’une variance nulle signifie aucune variation, donc toutes les observations $x_i$ ont la même valeur (ce qui est rare en pratique).
Exercice
On donne ci-dessous les notes de trois groupes d’étudiants :
Quelle est le groupe le plus hétérogène ?
On commence par calculer les moyenne de chaque groupe, que l’on notera $\overline{G1}, \overline{G2}$ et $\overline{G3}$ :
On remarque que $v_2 > v_3 > v_1$, le groupe le plus hétérogène est donc le groupe $G2$. Ce que l’on remarque, c’est que les groupes $G1$ et $G2$ ont des moyennes assez proches, et pourtant, leur variance est complètement différente. À l’avenir donc, ne vous fiez jamais à la moyenne, et effectuer un calcul de variance quasi-systématiquement dans vos études statistiques.
En conclusion, si l’on devait faire un tableau récapitulatif de toutes nos mesures, et surtout, leurs particularités :
| Mesure | Calcul algébrique | Sensibilité aux valeurs extrêmes | Différentiable | Utilisation |
|---|---|---|---|---|
| Moyenne | Oui | Oui | Oui | Très fréquente |
| Médiane | Non | Non | Non | Fréquente |
| Étendue | Oui | Oui | Non | Peu fréquente |
| Écart moyen absolu | Oui | Oui | Non | Peu fréquente |
| Variance | Oui | Oui | Oui | Très fréquente |
Mesure de forme
Nous avons vu comment résumer un échantillon avec une moyenne et comment mesurer sa dispersion avec la variance. Seulement voilà, il nous reste encore quelques mystères : les individus sont-ils plutôt concentrés à gauche de la moyenne, à droite ? La distribution est-elle uniforme, plate ou courbée ? Toutes ces questions motivent la création de mesures de forme, c’est-à-dire de mesures permettant d’identifier plus précisément la répartition des individus.
Les moments
L’outil qui sera le plus important pour mesurer la forme de la distribution est le moment. Il se définit dans un contexte plus général que la variance. On appelle moment d’ordre $p \in \mathbb{N}^*$ par rapport à $t \in \mathbb{R}$ la quantité suivante :
| Discrète | Continue agrégée | Continue non agrégée |
|---|---|---|
| $\displaystyle M_p^t=\sum_{i=1}^k f_i(a_i-t)^p $ | $\displaystyle M_p^t=\sum_{i=1}^k f_i(c_i-t)^p $ | $\displaystyle M_p^t=\frac{1}{n} \sum_{i=1}^k (x_i-t)^p $ |
Le moment d’ordre $p$ par rapport à $0$ s’appelle le moment simple d’ordre $p$ et sera noté $M_p$. Le moment d’ordre $p$ par rapport à $\overline{X}$ s’appelle le moment centré d’ordre $p$ et sera noté $\mu_p$. On utilise souvent le moment centré.
Démonstration
On ne démontre que dans le cas discret, car on procède de la même manière pour les autres cas. Remarquons que, en écrivant $M_1$, il s’agit de la moyenne de $X$. Pour le second terme :
Enfin, la dernière équation qui est très importante en probabilité et apparaît sous le nom de théorème de König-Huygens :
Mesures d’asymétrie
Commençons par déterminer s’il y a présence ou non d’une asymétrie : nous allons regarder si la distribution est orientée plutôt à gauche de la moyenne, ou à droite. Pour se faire une première idée, on a souvent tendance à regarder la position de la médiane par rapport à la moyenne. En effet, si $Med < \overline{X}$, on s’attends à ce que la distribution soit plutôt oblique à gauche, c’est-à-dire étalée à droite (on parle alors d’asymétrie positive). Si, au contraire, $Med > \overline{X}$, on s’attends à ce que la distribution soit plutôt oblique à droite et étalée à gauche (on parle alors d’asymétrie négative).
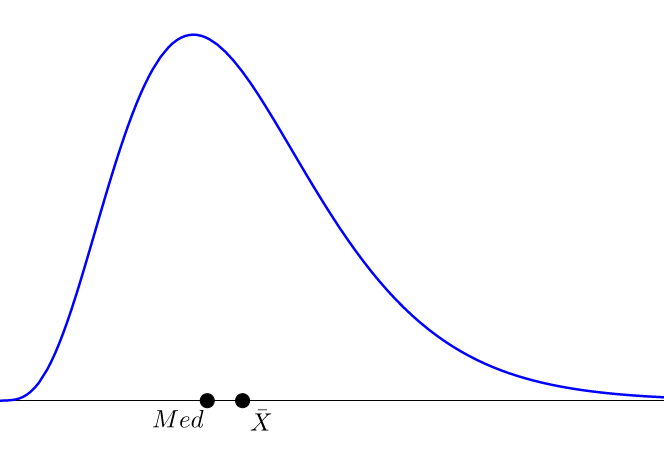
Pour comprendre, le graphe ci-dessus représente une distribution théorique (loi du $\chi^2$) qui présente une asymétrie positive : on a l’inégalité $Med < \overline{X}$, que l’on remarque bien sur le graphique puisque la distribution est étalée vers la droite.
Coefficient de Yule
Introduisons le coefficient de forme le plus intuitif, le coefficient de Yule :
Étudions cette quantité. On sait déjà, d’après les quantiles, que $Q1 \leq Med \leq Q3$. Ainsi, la quantité au dénominateur est toujours positive. Maintenant, regardons le numérateur : le cas où celui-ci s’annule est atteint lorsque $(Q3-Med)-(Med-Q1)=0$ soit
Or, lorsque $Med$ vaut exactement la moitié de la somme des premier et troisième quartiles, cela signifie qu’il y a autant d’observations en-dessous de $Q1$ qu’au-dessus de $Q3$. La distribution est alors parfaitement symétrique. Maintenant, dans le cas où $(Q3-Med)-(Med-Q1)<0$ alors
En particulier, cela signifie que les individus sont plus concentrés vers les fortes valeurs, d’où la distribution est oblique à droite, étalée à gauche. Si l’on récapitule :
- Si $S_Y=0$, alors la distribution est symétrique.
- Si $S_Y<0$, alors la distribution est oblique à droite, étalée à gauche.
- Si $S_Y>0$, alors la distribution est oblique à gauche, étalée à droite.
Coefficient de Fisher d’asymétrie
Le coefficient de Fisher d’asymétrie est fonction du moment centré d’ordre $3$ $\mu_3$ et de l’écart-type $\sigma$ :
Étudions le cas où $\gamma_1=0$. Pour plus de facilité, on traite uniquement le cas continu non agrégé et rappelons que :
Résoudre $\gamma_1=0$ consiste en réalité à résoudre $\mu_3=0$ mais on sait que :
Où $\varphi$ est toujours la bijection telle que la suite $(x_{\varphi(n)})$ soit croissante. Posons $q \in \{1, ..., n\}$. On a donc :
Puis, par identification :
Mais cette dernière égalité est valable pour tout $1 \leq q \leq n$, c’est-à-dire que l’écart par rapport à la moyenne portée par les $q$ premiers individus et l’opposée de celle portée par les $n-q$ autres individus. En balayant de $1$ jusqu’à $n$, puisque cette égalité est conservée, cela traduit une parfaite symétrie de la distribution. Par le même raisonnement, si $\gamma_1 < 0$, on aura :
Et la distribution sera oblique à droite, étalée à gauche. Allez, essayons de synthétiser tout ceci  :
:
- Si $\gamma_1=0$, alors la distribution est symétrique.
- Si $\gamma_1<0$, alors la distribution est oblique à droite, étalée à gauche.
- Si $\gamma_1>0$, alors la distribution est oblique à gauche, étalée à droite.
Pour apprécier la symétrie d’une distribution, on utilise la loi normale : c’est la loi de référence en théorie des probabilités, et l’on a souvent recours à la loi normale dite centrée réduite, d’espérance nulle (centrée) et de variance $1$ (réduite). Il est souvent intéressant de comparer notre distribution par rapport à cette loi, puisque cette dernière est parfaitement symétrique. Pour information, sa densité (i.e. sa loi de probabilité) en tout point $x$ de $\mathbb{R}$ est donné par :
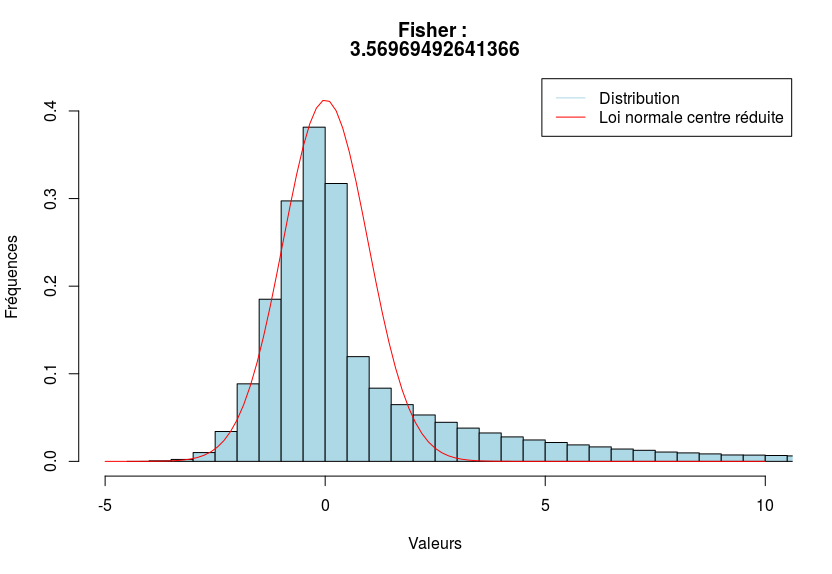
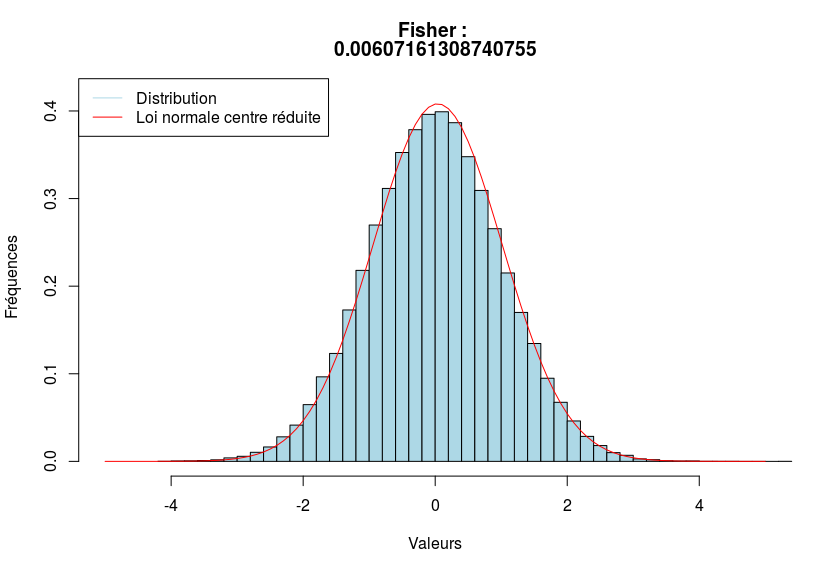
Où $\mu$ est l’espérance et $\sigma^2$ la variance. Par exemple, on dessine, en bleue, une distribution et en rouge, la loi normale centrée réduite.

Ci-dessous, trois exemples visuels afin de voir le coefficient de Fisher en action.

Mesure d’aplatissement avec les kurtosis
À présent, on souhaite également s’intéresser à l’aplatissement de la distribution, soit la concentration relative des observations autour de la valeur centrale.
Comment mesure-t-on objectivement l’aplatissement d’une distribution ?
Il a fallu, à un moment donné, définir mathématiquement ce que signifie aplati. En effet, tout est relatif : on peut trouver une distribution peu aplatie alors qu’en réalité, elle l’est beaucoup. Pour ce faire, on réalise une hypothèse de normalité, on considère que l’on peut estimer la distribution par une loi normale (je vous l’avais dit qu’elle était souvent utilisée  ).
).
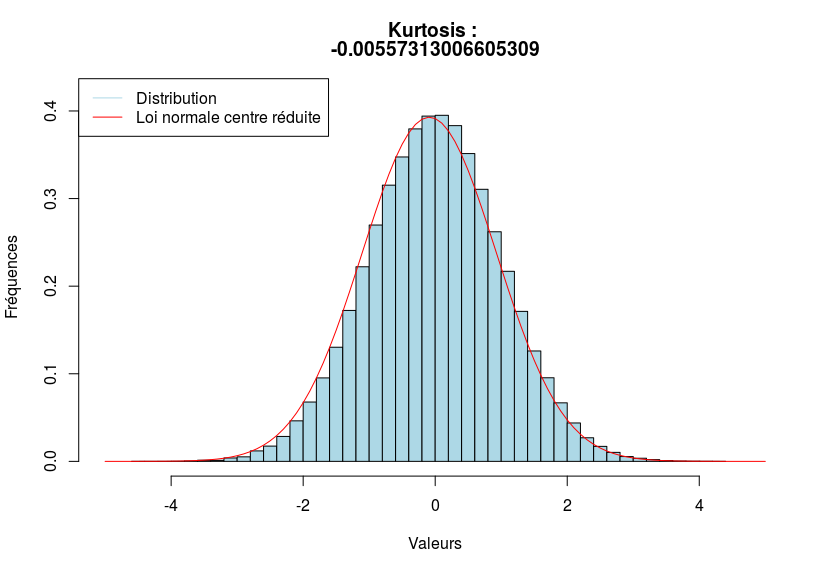
On étudie alors la manière dont la distribution est répartie en fonction de l’hypothèse de normalité. Pour cela, les statisticiens adorent utiliser des mots savants à la place de plat ou concentré  . On dira qu’une distribution est
. On dira qu’une distribution est
- Mésocurtique si les observations sont aussi concentrées que sous l’hypothèse de normalité.
- Platicurtique si les observations sont moins concentrées que sous l’hypothèse de normalité.
- Leptocurtique si les observations sont plus concentrées que sous l’hypothèse de normalité.
On appelle kurtosis non normalisé la quantité $\beta_2$ comme étant le rapport entre le moment centré d’ordre $4$ $\mu_4$ et la variance élevée au carré :
Par exemple, ci-dessous, on donne trois distributions, la première étant platicurtique, la seconde mésocurtique et la dernière, leptocurtique.


Sachez qu’en règle général, on utilise plutôt le kurtosis normalisé. Je ne rentrerais pas dans les détails, puisque les calculs font intervenir les cumulants.
Mesure de concentration
Nous avons presque terminé notre panel de mesures. Seulement je souhaitais vous faire découvrir une dernière catégorie de mesures, appelées mesure de concentration, qui sont souvent utiles notamment lorsqu’il s’agit de comparer des richesses au sein d’un échantillon. Seulement, pour comparer cette richesse, la fréquence cumulée à elle seule ne suffit plus : il nous faut introduire la fréquence cumulée $\tilde{F}$ relative aux $n_ix_i$. En effet, l’objectif sera de comparer $F_i$ et $\tilde{F}_i$. Plus l’écart sera grand, plus la richesse sera répartie de manière inégale.
Lorsque l’on emploie le terme richesse, il peut s’agir de richesse en terme d’argent mais pas uniquement ! Comme nous le verrons dans l’exercice d’application, une richesse peut également désigner une surface d’exploitation ou encore une part.
Il faut garder en tête que richesse signifie plutôt "ce que possède" un individu. Définissons ainsi cette fréquence cumulée $\tilde{F}$.
| Discrète | Continue agrégée | Continue non agrégée |
|---|---|---|
| $\displaystyle \tilde{F}_i=\sum_{k=1}^i \frac{f_k a_k}{M} \text{ avec } M=\sum_{i=1}^k f_i a_i$ | $\displaystyle \tilde{F}_i=\sum_{k=1}^i \frac{f_k c_k}{M} \text{ avec } M=\sum_{i=1}^k f_i c_i$ | $\displaystyle \tilde{F}_i=\sum_{k=1}^i \frac{n_k x_k}{M} \text{ avec } M=\sum_{i=1}^n n_i x_i$ |
Ici, notre masse $M$ représente donc la somme de toutes les valeurs prises par la variable pondérées par les effectifs. N’oubliez pas que dans les cas discret et continue agrégée, on dispose de $k$ classes alors que dans le cas continu non agrégé, nous avons $n$ individus. 
L’indice de Gini et courbe de Lorenz
L’indice de Gini $G$ est défini comme deux fois la surface comprise entre la droite d’équi-répartition et la courbe de concentration.
Je traite uniquement le cas d’une variable continu non agrégée, mais le résultat est similaire pour les deux autres cas : on fera attention à considérer $k$ et non plus $n$.
Pour ce faire, on représente la succession de points $(F_i ; \tilde{F}_i)$ par une fonction $f$ continue de $[0,1]$ dans $[0,1]$, affine par morceaux et telle que, pour tout $0 \leq i \leq n, f(F_i)=\tilde{F_i}$. On appelle alors $f$ la courbe de Lorenz. On veut donc calculer :
Car $x \geq f(x), \forall x \in [0,1]$. C’est ainsi que l’on subdivise l’intervalle $[0,1]$ en $n$ subdivisions :
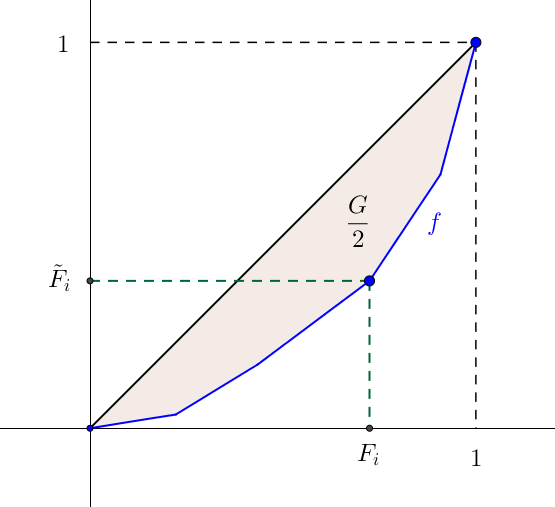
L’idée est, dans un premier temps, de déterminer l’intégrale de $f$ sur $[0,1]$ par la méthode des trapèzes pour ensuite en déduire l’indice de Gini. Pour tout $0 \leq i \leq n$, la surface comprise entre la courbe $f$ et délimitée par les droites d’abscisse $x=F_i$ et $x=F_{i+1}$ est :
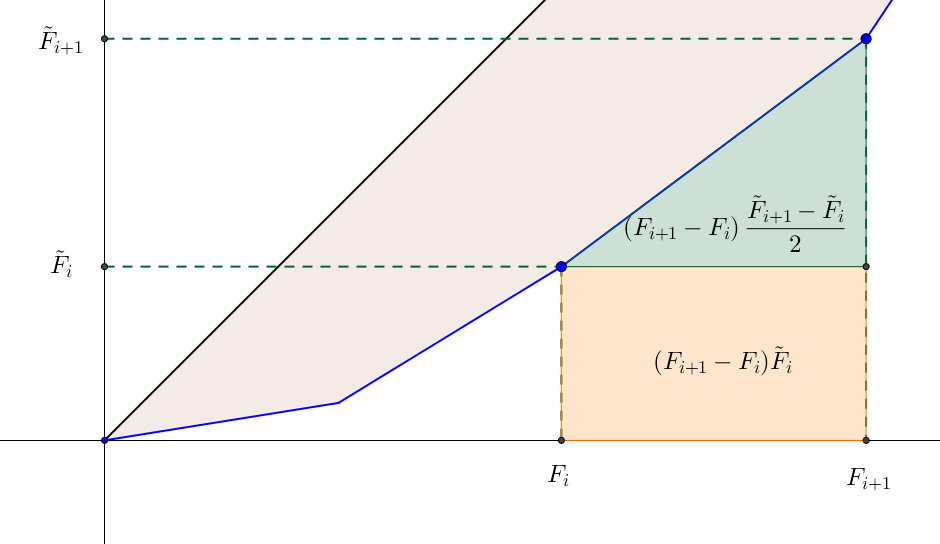
À noter qu’ici, la méthode des trapèzes fournit la valeur exacte puisque $f$ est affine par morceaux. Mais $F_{i+1}-F_i=\frac{n_{i+1}}{n}$ et $f(F_i)=\tilde{F}_i$, pour tout $0 \leq i \leq n$ d’où
Et donc, la surface totale est vue comme la somme des aires :
Or l’aire sous la courbe d’équi-répartition vaut $\frac{1}{2}$, l’indice de Gini étant défini comme le double de cette différence avec l’aire sous la courbe des fréquences cumulées $\tilde{F}_i$ :
Avec $F_0=\tilde{F}_0=0$. Pour résumer, l’indice de Gini s’exprime ainsi de cette manière :
| Discrète | Continue agrégée | Continue non agrégée |
|---|---|---|
| $\displaystyle G=1-\sum_{i=1}^{k} f_i(\tilde{F}_{i}+\tilde{F}_{i-1})$ | $\displaystyle G=1- \sum_{i=1}^{k} f_{i}(\tilde{F}_{i}+\tilde{F}_{i-1})$ | $\displaystyle G=1-\frac{1}{n} \sum_{i=1}^{n} n_i(\tilde{F}_{i}+\tilde{F}_{i-1})$ |
Pour interpréter ce coefficient, il suffit de regarder sa valeur qui se situe entre $0$ et $1$ :
- Si $G=0$, nous sommes face à un cas où la distribution des richesses et parfaitement égalitaire : chaque individu possède la même part de richesse. Dans une entreprise, cela signifie que tous les employés ont exactement le même salaire.
- Si $G=1$, il y a alors une parfaite inégalité : un seul individu possède exactement la richesse de tous les autres individus. Par exemple, dans une entreprise, cela signifierai qu’un employé posséderait exactement les salaires de tous les autres employés, et que ces derniers ne recevraient rien (bien entendu, il s’agit d’un exemple abstrait, ce cas est figure est heureusement impossible dans la réalité).
- Si $0 < G < 1$, il faut alors interpoler par rapport aux deux valeurs précédentes. Plus $G$ est proche de $0$, plus la distribution des richesses est égalitaire. À l’inverse, plus $G$ est proche de $1$, plus la distribution des richesses est inégale.
Représentations graphiques
Dans cette dernière partie, nous allons explorer différentes méthodes pour représenter graphiquement une distribution. Bien sûr, je ne vous présente pas toutes les représentations existantes, il me faudrait un tutoriel en entier pour vous les présenter. En revanche, je vous propose de découvrir les représentations graphiques les plus utilisées, et surtout les plus commodes. 
Diagramme en bâtons
Ce diagramme est sans doute celui que vous utilisez le plus souvent. En plus d’être facile à comprendre, il permet de déterminer rapidement la forme et la répartition d’une distribution. Pour chaque modalité $a_i$ (ou chaque classe $[a_i, a_{i+1}[$), on fait correspondre un rectangle de largeur constante et de hauteur proportionnelle à la fréquence :
Où $c \in \mathbb{R}_+^*$ est une constante. Par exemple, si l’on souhaite afficher les effectifs plutôt que les fréquences, on choisira $c=n$.
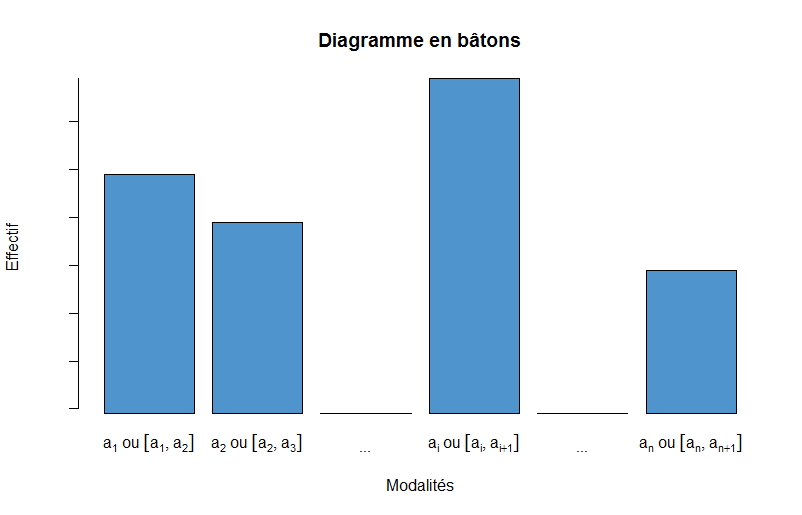
Diagramme en secteurs
Aussi appelé diagramme circulaire, il joue le même rôle que le précédent, à la différence où cette fois-ci, les fréquences ne sont plus affichées selon des rectangles mais par des secteurs d’angles proportionnels à la fréquence. Ainsi, chaque secteur a pour angle (en radians) :
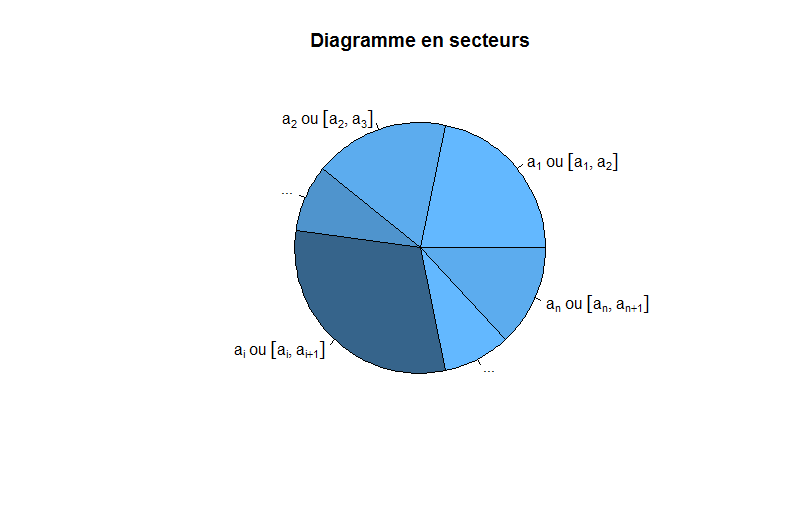
Dans les faits, je vous déconseille d’utiliser cette représentation si les données "ne s’y prêtent pas".
Par exemple, je dispose d’un ensemble de données, puis je décide d’afficher un diagramme en secteurs pour visualiser les proportions. J’obtiens ce diagramme

Comme vous pouvez le remarquer, cette représentation est très mauvaise dans ce cas : près de $75$ % du disque ne représente qu’une seule fréquence, alors que toutes les autres sont représentées sur $25$ % du disque. Comment comparer toutes les autres fréquences ? C’est là qu’interviennent les limitations de cette représentation. Ainsi, n’utilisez le diagramme en secteurs que si
- Il n’y a pas beaucoup de classes ou fréquences à considérer
- Les fréquences sont globalement bien réparties (on ne veut pas qu’une seule classe monopolise tout le diagramme)
Histogramme
On utilise souvent l’histogramme pour des variables continues agrégées. Le principe de construction ressemble à celui du diagramme en bâtons, mais la différence réside dans le fait que la largeur des rectangles n’est plus forcément constante : elle dépend de la longueur des classes. En effet, chaque rectangle aura pour largeur $L_i$ et pour hauteur $h_i$ :
De sorte que la surface $S_i=c \times f_i$ soit proportionnelle à la fréquence, avec $c \in \mathbb{R}_+^*$.

Il n’existe pas de méthodes absolues pour définir le nombre de classes $k$ à utiliser. Néanmoins, on utilise certains critères comme la règle de Sturges permettant de déterminer le nombre de classes $k$ à utiliser pour $n$ individus :
Boîtes à moustache
Derrière ce petit nom sympathique se cache une représentation très intéressante lorsqu’il s’agit de détecter les valeurs aberrantes. L’idée de construction est la suivante :
- On construit une boîte entre $Q1$ et $Q3$ (donc de longueur $EIQ$).
- On détermine à présent les moustaches : l’extrémité de la moustache inférieure $A$ est la plus petite valeur $x_i$ telle que $x_i \geq Q1-1,5 EIQ$.
- L’extrémité de la moustache supérieure $B$ est la plus grande valeur $x_i$ telle que $x_i \leq Q3+1,5 EIQ$.
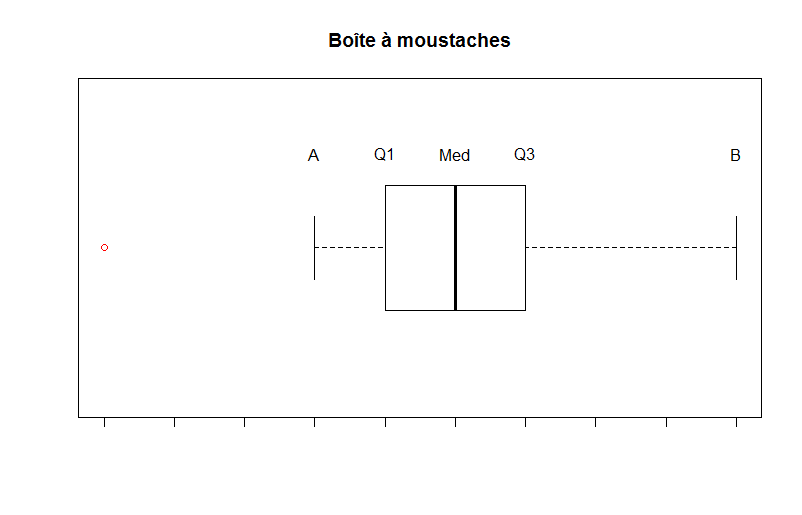
Comme vous pouvez le constater sur cet exemple, le point rouge est un point aberrant, car il est situé en dehors du rectangle et des moustaches sous l’hypothèse de normalité.
Pourquoi utilisons-nous $1,5$ dans les extrémités des moustaches ?
Cela vient du fait que le modèle est basé sur la distribution d’une loi normale. Si une variable suit une loi normale, alors l’intervalle $[A, B]$ devrait contenir $99,3$ % des observations, c’est-à-dire que l’on devrait trouver $0.7$ % d’observations en dehors de l’intervalle $[A, B]$, que l’on considère alors comme des valeurs aberrantes. Pour le créateur de cette représentation, John Tukey, $1,5$ était un bon compromis pour observer assez de points aberrants, sans pour autant en être débordé.
Exercice d'application
Enfin, toute la théorie est terminée  ! Afin de mettre en pratique tout ce que vous avez appris au cours de ce tutoriel, je vous propose ainsi un exercice qui va faire appel à la plupart des notions introduites précédemment. Bien sûr, n’hésitez pas à remonter si vous avez oublié une formule, je vous y encourage
! Afin de mettre en pratique tout ce que vous avez appris au cours de ce tutoriel, je vous propose ainsi un exercice qui va faire appel à la plupart des notions introduites précédemment. Bien sûr, n’hésitez pas à remonter si vous avez oublié une formule, je vous y encourage 
Le sujet
Dans une certaine région, on donne le nombre d’exploitations agricoles par surface agricole utile, exprimée en hectares.
| Surface agricole utile (SAU) | < 5 | 5 à 10 | 10 à 20 | 20 à 50 | 50 à 100 | > 100 |
|---|---|---|---|---|---|---|
| Nombre d’exploitations | 7800 | 9600 | 13200 | 20400 | 7200 | 1800 |
- De quel type de variable s’agit-il ? Représentez graphiquement la distribution et calculez le milieu des classes $c_i$.
- Déterminez la moyenne, la variance et l’écart-type de l’échantillon.
- Calculez la médiane et l’écart inter-quartile. D’après ces deux informations, la distribution semble-t-elle symétrique ?
- Vérifiez votre réponse avec le coefficient de Yule.
- Pourrait-on dire que la distribution est aussi concentrée que sous l’hypothèse de normalité ?
- Déterminez l’indice de Gini. Que peut-on dire de la répartition des richesses dans cet échantillon ?
Correction
En plus d’effectuer les calculs, je vous donne le code R associé pour que vous puissiez vous même essayer de développer un programme sous R.
1) Ici, notre variable est la surface agricole utile (SAU). Il s’agit donc d’une variable quantitative (ici, un nombre réel) et qui est également agrégée, car nous disposons des classes suivantes :
À noter que pour la dernière classe, j’ai moi-même utilisé la valeur $200$ puisque la dernière classe n’est pas correctement définie. On veillera ainsi à prendre une borne cohérente. En calcule alors le milieu de chacune de ces classes :
On représente alors la distribution :
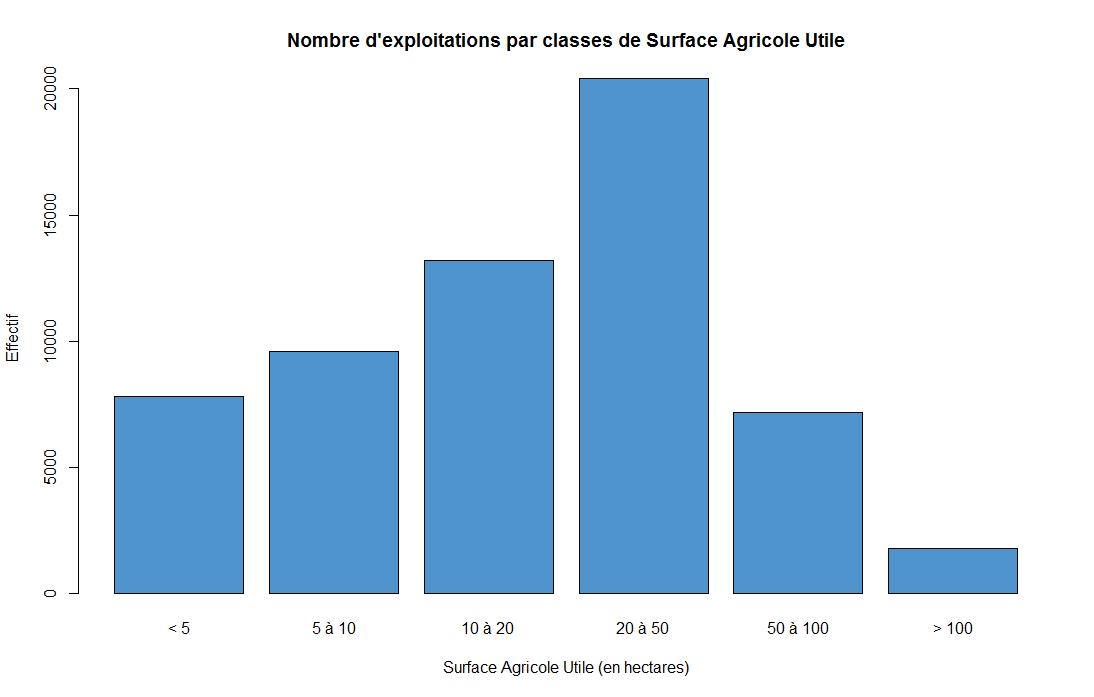
1 2 3 4 5 | nb<-c(7800,9600,13200,20400,7200,1800) # Le nombre d'exploitations par classes
bornes<-c(0,5,10,20,50,100,200) # Les bornes de nos classes
ci<-(bornes[-7]+bornes[-1])/2 # Le milieu des classes
ci
barplot(nb,main="Nombre d'exploitations par classes de Surface Agricole Utile",names.arg=c("< 5","5 à 10","10 à 20","20 à 50","50 à 100","> 100"),col="steelblue3",xlab="Surface Agricole Utile (en hectares)",ylab="Effectif")
|
2) Notons $m$ la moyenne de l’échantillon et $v$ sa variance. Ici, notre effectif total est $n=7800+9600+13200+20400+7200+1800=60000$, ce qui nous permet de calculer les fréquences $f_i$ :
En notant $\sigma$ l’écart-type, on calcule alors $\sigma=\sqrt{v}=30.20367$. Pour récapituler :
1 2 3 4 5 6 7 8 9 | n<-sum(nb) # Le nombre total d'individus f<-nb/n # Les fréquences f m<-sum(ci*nb)/n # La moyenne m v<-sum(f*(ci-m)^2) # La variance v sigma<-sqrt(v) # l'écart-type sigma |
3) Notons $F$ la fréquence cumulée alors :
On remarque alors que $10 < Med < 20$ car $F_2 < 0,5 < F_3$. Pour cela, on applique la formule d’interpolation linéaire :
En notant $Q1$ et $Q3$ le premier et le troisième quartile, on remarque que $5 < Q1 < 10$ et $20 < Q3 < 50$ donc :
On en déduit alors l’écart inter-quartile $EIQ=Q3-Q1 \approx 32,43$. On remarque que $Med < \frac{Q1+Q3}{2} \approx 24,965$, ce qui indique que la distribution serait plutôt oblique à gauche, aplatie à droite.
4) On calcule le coefficient de Yule $S_Y$ de la distribution :
On a $S_Y>0$, ce qui valide notre hypothèse précédente affirmant que la distribution est oblique à gauche. Ce calcul permet de confirmer ce que l’on voit sur le graphique de la distribution.
5) Pour répondre à cette question, il nous faut calculer le kurtosis normalisé de la distribution, que l’on note $\gamma_2$. Pour rappel,
On connait déjà la variance, alors calculons le moment centré d’ordre $4$ $\mu_4$ :
Et donc
En conclusion, la distribution est beaucoup plus concentrée que sous l’hypothèse de normalité.
1 2 3 4 | mu4<-sum(f*(ci-m)^4) # Moment centré d'ordre 4 mu4 kurtosis<-mu4/v^2-3 kurtosis |
6) On note $\tilde{F}$ la fréquence cumulée relative aux $n_i x_i$ ce qui nous donne :
On applique alors la formule pour déterminer le coefficient de Gini :
En somme, cela signifie qu’une certaine partie des exploitations comptabilise, à elle seule, une majeure partie de la SAU. Et cela se remarque très bien sur le graphique de la distribution : seulement une petite quantité d’exploitations dispose plus de 50 hectares de SAU ! Alors d’un grand nombre d’exploitations ($51 000$ exactement) possèdent moins de 50 hectares de SAU. Globalement, on peut conclure qu’il existe une certaine inégalité en terme de SAU. Toutefois, nous ne disposons pas assez d’informations pour parler réellement d’une inégalité : on ne connait ni la production de chaque exploitation, ni la localisation, qui sont des facteurs importants. On se contera alors d’émettre l’hypothèse d’une inégalité moyenne selon nos observations. On fournit, ci-dessous, le graphique représentant cette courbe des richesses.
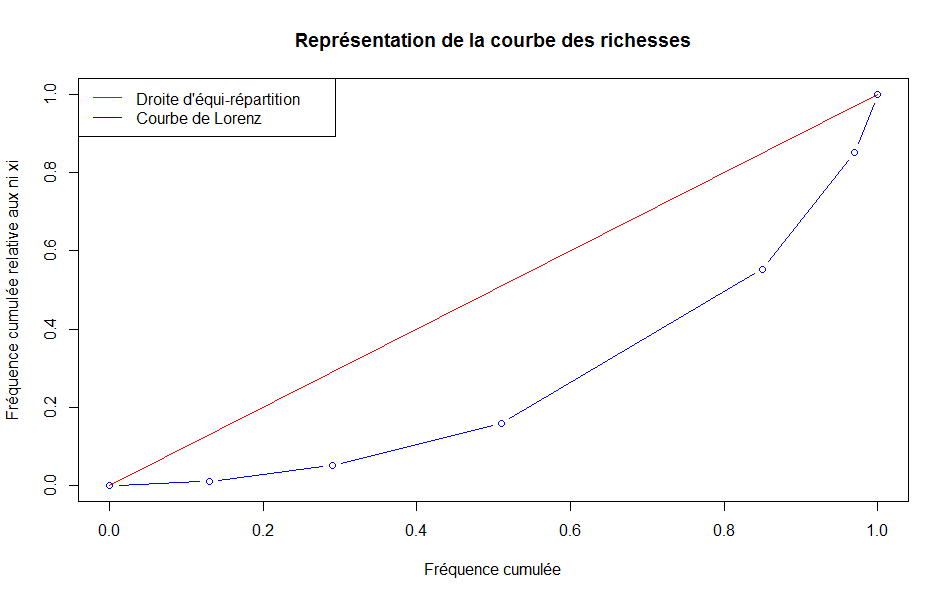
1 2 3 4 5 6 7 8 9 10 11 | Fc<-cumsum(f) # La fréquence cumulée
Fc
fm<-f*ci/sum(f*ci) # Fréquence relative aux nixi
Fm<-cumsum(fm) # Fréquence cumulée relative aux nixi
Fm
IG<-1-sum(f*(c(0,Fm[-6])+Fm)) # Coefficient de Gini
IG
plot(c(0, Fc), c(0, Fm),type="b",col="blue",xlab="Fréquence cumulée",ylab="Fréquence cumulée relative aux ni xi", main="Représentation de la courbe des richesses")
lines(c(0, 1), c(0, 1), col="red")
legend("topleft", legend=c("Droite d'équi-répartition", "Courbe de Lorenz"), col=c("red", "blue"), lty=1)
|
Félicitations pour être arrivé jusqu’ici  .
Même si ce tutoriel ne présente pas toutes les notions de la statistique descriptive à une dimension, vous aurez tout de même une solide base pour explorer le merveilleux monde de la statistique. En résumé de ce cours :
.
Même si ce tutoriel ne présente pas toutes les notions de la statistique descriptive à une dimension, vous aurez tout de même une solide base pour explorer le merveilleux monde de la statistique. En résumé de ce cours :
- Définition d’un vocabulaire rigoureux régulièrement utilisé en statistique
- Liste des types de variables existantes, même si nous avons uniquement étudié les variables quantitatives
- Beaucoup de mesures ont été présentées : tendance centrale, forme des distributions, dispersion autour de la moyenne, ou encore de richesse.
- Plusieurs représentations des données ont été montrées, et notamment celles qui sont particulièrement utilisées
- Pour finir, un exercice d’application pour clôturer ce cours.
Sachez qu’à présent, de nouvelles voies s’offrent à vous :
- La statistique descriptive à deux dimensions, qui s’inscrit dans la continuité de ce tutoriel. Vous l’aurez compris, il s’agit d’étudier non pas une mais deux variables à la fois.
- La statistique descriptive multidimensionnelle : dès que l’on commence à étudier trois variables ou plus, on fait ce que l’on appelle de la statistique descriptive multidimensionnelle. En particulier, on utilise des méthodes d’analyse factorielle (ACP, AFC, …) et de classification pour résumer au mieux l’information de $p$ variables sur $n$ individus.
- Les séries temporelles, où l’on étudie les phénomènes qui dépendent du temps, et notamment ceux disposant de cycle saisonniers.
- La statistique inférentielle, où l’objet des études est d’effectuer des hypothèses sur une population à partir d’un échantillon.
Si vous remarquez la moindre erreur ou tout simplement si vous avez une remarque concernant ce tutoriel, n’hésitez pas à me contacter par message.