Introduction au traitement d'image

Dans ce tutoriel nous allons voir ensemble comment traiter des images avec le langage de programmation Python. Le but n’est pas d’obtenir un logiciel Photoshop-like mais de comprendre le fonctionnement des opérations réalisées. Nous allons couvrir dans ce tuto les opérations les plus courantes du traitement d’images.

Les exemples donnés seront écrit en Python, mais peuvent être réalisés dans n’importe quel autre langage de programmation. Nul besoins de connaître le langage Python pour comprendre l’ensemble du contenu, le code va être très simple et le but est surtout de comprendre les opérations.

Prêts ? C’est parti !

• Manipuler notre image
• Les manipulations du point
• Les manipulations de l'image

Manipuler notre image

SciPy et Numpy

Dans ce tuto nous allons manipuler les images à l’aide de deux bibliothèques Python : SciPy et Numpy. Il est possible dans d’autres langages d’utiliser des bibliothèques équivalentes. SciPy est un ensemble de bibliothèques regroupant de nombreux outils scientifiques pour l’algèbre, les statistiques ou encore … le traitement d’image. Numpy est une extension du langage Python incluse dans la suite SciPy. Pour les installer rien de plus simple, on utilise pip (guide d’installation) avec la commande :

pip install --user numpy scipy

Si vous souhaitez installer l’ensemble des outils de la suite vous pouvez opter pour :

pip install --user numpy scipy matplotlib ipython jupyter pandas sympy nose

Manipuler une image

Maintenant que les outils sont installés nous allons apprendre à manipuler une image. C’est-à-dire la lire et l’enregistrer pour que l’on puisse ensuite faire des modifications. Pour cela rien de plus simple :

1
2
3
4

import scipy.misc
import numpy as np

im = scipy.misc.imread('input.jpg', True)

Quelques remarques sur ce code :

• On commence par importer les bibliothèques que nous avons installées à l’étape précédente.
• On ouvre notre fichier grâce à la fonction imread. Cette fonction ouvre une image depuis un fichier et renvoi un tableau contenant les pixels de notre image. Plus de trente formats sont compatibles avec imread : JPEG, JPEG2000, GIF, PNG, BMP, TIFF… Vous devriez trouver votre bonheur facilement.
• On passe True en paramètre à la fonction pour travailler en nuances de gris. On commence simplement avant d’introduire la couleur. Pour plus de détails : rendez-vous sur la doc.

Maintenant que nous savons lire, apprenons à écrire, pour cela on utilise la fonction imsave, plutôt basique.

1
2
3
4
5
6
7
8

import scipy.misc
import numpy as np

im = scipy.misc.imread('lena.bmp', True)

# Ici, on traite notre image

scipy.misc.imsave('output.png', im)

Il suffit de donner un nom et une extension ainsi que la variable contenant l’image pour l’enregistrement se fasse correctement. Vous noterez que je lis une image au format BMP et que j’enregistre une image au format PNG, la conversion est implicite. Le résultat obtenu est bien une image en nuance de gris.

Les manipulations du point

Dans cette partie nous allons étudier les manipulations effectuées pixel par pixel sur l’image. Ce sont les opérations les plus simples à réaliser, mais permettent déjà des résultats amusants.

La seule valeur que nous ayons pour les pixels est la luminosité. Si vous avez déjà fait un peu de retouche d’image vous pouvez facilement deviner les effets que nous pouvons réaliser :

• Augmentation / diminution de la luminosité
• Augmentation / diminution du contraste
• Seuillage

Jouer avec la luminosité

Pour modifier la luminosité de notre image, rien de plus simple, il suffit de modifier la valeur des pixels. On peut par exemple ajouter une valeur constante sur toute l’image :

1
2

im += 100
im = np.clip(im, 0, 255)

On ajoute dans cet exemple une valeur de 100 à tous les pixels de l’image. On utilise ensuite la fonction clip pour s’assurer que la valeur des pixels soit contenue dans l’intervalle $[0; 255]$. En effet, chaque valeur de luminosité de l’image est codée sur 8 bits et sa valeur est donc limitée. Voici le résultat obtenu :

Comme on peut le constater notre image a bien gagné en luminosité, mais on a aussi perdu de nombreux détails dans les zones les plus claires. En effet les pixels de l’image d’origine qui avaient une valeur de luminance de 200 se retrouvent avec une valeur de 300, puis sont limités à 255 par le clipping. On perd donc en détails dans les hautes lumières à cause de l’écrêtage du signal. Il en va de même si on réduit de manière trop importante la luminosité.

1
2

im -= 125
im = np.clip(im, 0, 255)

Jouer avec le contraste

La modification de luminosité faisait appel à des soustractions et des additions, la modification du contraste va quant à elle fonctionner grâce à des … multiplications. En effet en multipliant les coefficients par une valeur on va réaliser un contrast streching ou étirement de contraste. En sachant cela il est facile de deviner comment procéder. On obtient un résultat de ce type.

1
2

im = np.multiply(im, 1.5)
im = np.clip(im, 0, 255)

De nouveau on utilise le clipping pour rester dans la zone de valeur autorisée, mais de nouveau cela provoque de l’écrêtage qui nous fait perdre de l’information dans les zones lumineuses. On voit bien sur que le contraste global de l’image a été augmenté. Pour éviter la perte d’information du à l’écrêtage après le contrast streching il existe une autre méthode de modification de contraste qui s’appelle l’égalisation d’histogramme. Cette autre méthode sera traitée dans la partie suivante.

Seuillage

Une autre opération rigolote consiste à seuiller notre image. On parle souvent de threshold en anglais. Le principe est d’établir une valeur limite de luminosité, toute valeur en dessous prend une valeur faible, toute valeur supérieure prend une valeur haute. L’image résultant ne contient plus que deux niveaux de valeur. Nous allons pouvoir réaliser cette opération très facilement à l’aide de la fonction where :

1

im = np.where(im > 100, 255, 0)

On passe d’abord notre condition, ici on s’intéresse à tous les pixels dont la luminosité est supérieur à 100 et on passe ensuite les valeurs en cas de condition vraie et fausse.

Si on écrit un pseudo code pour mieux comprendre ce que fait cette fonction, on obtient quelque chose comme ça:

1
2
3
4
5

POUR CHAQUE PIXEL DE L'IMAGE
    SI LA VALEUR DU PIXEL EST SUPÉRIEUR A 100
        ALORS ATTRIBUER LA VALEUR 255 AU PIXEL
    SINON
        ATTRIBUER LA VALEUR 0 AU PIXEL

Le résultat est le suivant.

Rien ne m’oblige à travailler avec les valeurs extrêmes de l’intervalle et je peux par exemple réaliser l’opération suivante :

1
2

im = np.where(im > 100, 200, 100)
scipy.misc.toimage(im, cmin=0, cmax=255).save("output.png")

Notez le changement dans la sauvegarde l’image. La fonction que nous utilisions jusqu’ici pratique un auto-scale des valeurs, c’est à dire qu’elle modifie notre image pour que celle-ci utilise la plus grande plage de valeur possible. Avec cette nouvelle fonction, cet étirement des données est désactivé, ce qui nous permet de nous rendre compte de la modification apportée.

On se sert notamment du seuillage pour segmenter une image, c’est à dire découper une image en plusieurs espaces distinct. Notre approche est très simpliste car elle se base uniquement sur la luminosité (en ignorant les formes, les contours, etc.). Néanmoins le seuillage permet de réussir à séparer deux objets dans des cas particuliers. Prenons par exemple l’image suivante :

Nous pouvons avec im = np.where(im > 115, 250, 0) obtenir ce résultat :

Alors bien sûr cette méthode ne fonctionne pas pour toutes les images, mais permet dans certains cas d’obtenir une segmentation très simple. Ici il ma fallut quelques tentatives pour trouver la bonne valeur . Vous pouvez en utilisant les masks très facilement remplacer le ciel par un autre.

Pour aller plus loin

Si vous souhaitez continuer à creuser ce type d’opérations avec des images, voici quelques pistes :

• Réaliser des sommes pondérées entre deux images. On peut imaginer réaliser une image correspondant à 0,3 Image_A + 0,7 Image_B. Le résultat est alors une sorte de fondu entre deux images : utile pour comparer visuellement deux photos.
• Réaliser des opérateurs binaires entre deux images. Cela permet d’extraire les pixels commun à A ET à B ou de dessiner l’image NON A (l’inverse de A), etc. Ce genre d’opération est par exemple utile pour trouver les pixels différents entre deux images semblables.

Les manipulations de l'image

Dans cette section nous allons traiter de toutes les modification de l’image dans son ensemble (ou dans une zone) et non plus uniquement à des valeurs isolées de pixels. Cette partie est plus complexe aussi bien pour l’algorithmie que pour les maths, mais rien d’impossible !

Agrandissons !

On commence sagement avec les modifications liées à la taille de l’image. On s’intéresse ici aux homothéties, c’est-à-dire les transformations qui conservent le rapport de proportion original (le "format"). Pour agrandir une image d’un facteur 2, rien de plus simple :

1

im = scipy.misc.imresize(im, 2.0, 'nearest')

Vous pouvez voir que je passe un troisième paramètre qui me permet de choisir le mode d’interpolation que je veux choisir. Le mode d’interpolation permet de choisir avec quel algorithme la bibliothèque va agrandir notre image, car oui il existe plusieurs façons d’agrandir une image.

Nearest Neighbor

La méthode nearest neighbor que nous avons utilisé dans l’exemple précédent est la méthode la plus simple d’un point de vue algorithmique. Le résultat est assez mauvais, mais le code s’exécute très rapidement en comparaison des autres techniques. Pour agrandir une image cet algorithme fonctionne la manière suivante :

• Prendre l’image de départ.
• Calculer la taille de l’image de destination (en fonction d’un facteur par exemple).
• Introduire des pixels noirs dans l’image de départ afin d’obtenir une image à la bonne taille, (cliquez ici pour voir un exemple en image).
• Remplir les pixels noirs introduits en recopiant la valeur du pixel le plus proche.

Dans le cas d’un agrandissement d’un facteur 2, c’est assez simple car il suffit d’introduire une ligne et une colonne sur deux de pixels noirs. En revanche dans les autres cas l’algorithme doit décider à quel endroit introduire ces pixels supplémentaires. Comme vous le voyez la méthode reste assez simple et ne comprend de calculs de pixels à proprement parler. Si vous deviez implémenter un agrandissement rapide pour lequel la vitesse prime, comme dans le cas d’un vieux navigateur web ou d’une télévision bas de gamme vous choisiriez cette méthode.

Linear et Bi-linear

On passe à une méthode légèrement plus compliquée, l’interpolation linéaire. Cette fois-ci pour combler le pixel noir l’algorithme ne va pas bêtement recopier un pixel, mais réaliser une moyenne. Le résultat pour un pixel est la moyenne (non-pondérée) de deux voisins (horizontaux ou verticaux). Cette méthode est à peine plus complexe mais nécessite tout de même un peu plus de temps de calcul : accès à deux valeurs, somme, division puis assignation du résultat.

Mais quitte à utiliser les pixels voisins autant pousser la moyenne un peu plus loin, non ? C’est l’interpolation bi-linéaire. Elle se base sur le même principe mais réalise une moyenne sur 4 pixels, le résultat est visuellement meilleur, mais le temps de calcul plus long. Par défaut la bibliothèque utilise la méthode bilinéaire, on peut l’utiliser ainsi :

im = scipy.misc.imresize(im, 2.0)

Pour confirmer ce résultat visuel nous pouvons de nouveau tester avec un facteur plus difficile à traiter.

Comme dit précédemment cet algorithme est un peu plus lent que le précédent. Si je réalise 100 fois l’agrandissement d’une image pour chaque algorithme j’obtiens les résultats suivants :

1
2
3
4

python timing_nearest.py 
function took 1460.185 ms
python timing_bilinear.py
function took 2513.666 ms

On voit que le deuxième algorithme est plus lent, il prend environ 1 seconde de plus pour traiter cent images. Cette "lenteur" n’est pas importante dans beaucoup d’applications mais peut être embêtante en cas de faible puissance de calcul ou d’un besoin de très faible latence.

Alors bien sûr il existe encore d’autres algorithmes d’interpolations, je vous laisse allez voir du côté de wikipédia si vous souhaitez en savoir plus. En approfondissant le sujet, vous vous rendrez compte que certains algorithmes sont meilleurs sur certains types d’images et qu’il n’existe pas de solution parfaite, mais seulement un compromis qualité / temps de calcul.

Égalisation d’histogramme

On en avait parlé dans le chapitre précédent, maintenant voyons comment fonctionne cet algorithme. En traitement d’image nous utilisons souvent les histogrammes qui permettent de savoir comment sont répartis les pixels de l’image dans l’échelle de la luminosité. Ça ressemble à ça :

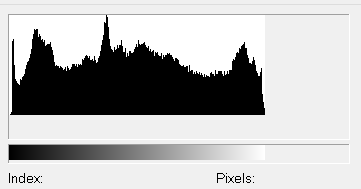
Sur l’axe des abscisses on retrouve l’ensemble des valeurs de luminosité possible et sur l’axe des ordonnées la fréquence rencontrée pour une valeur. L’objectif de l’égalisation d’histogramme est de faire en sorte que le résultat soit plat. En théorie c’est réalisable, dans les faits on ne peut qu’approximer ce résultat. Pour cela on va construire l’histogramme de notre image puis corriger les valeurs des pixels pour changer la distribution de la luminosité sur l’histogramme. Pour ce faire regardons de plus près la méthode histogram de Numpy:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

# Imaginons une image très simple de 4 pixels x 1 pixel
a = [0, 0, 0, 1]

# La fonction renvoi un couple de valeur
hist, bins = np.histogram(a)

# La première compte les fréquences d'apparition de chaque valeur
print(hist)
[3, 0, 0, 0, 0, 0, 0, 0, 0, 1]

# La deuxième contient les valeurs trouvées dans l'image
print(bins)
[ 0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ]

Dans cet exemple nous obtenons donc les valeurs (réparties entre 0 et 1) et un nombre d’apparition comprit entre 0 et 3. On peut passer en paramètres de la fonction histogram le nombre de données que l’on souhaite obtenir ainsi que la place de répartition de celles-ci. Par exemple :

1
2
3
4
5
6
7
8

hist, bins = np.histogram(b, 256, [0,256])
print(hist)
[3, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ..., 0]

print(bins) 
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ... , 255]

`

Essayons d’utiliser ces informations pour améliorer notre image.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

img = scipy.misc.imread('lena_abimee.png', 0)

hist, bins = np.histogram(img.flatten(), 256, [0, 255])

cdf = hist.cumsum()
cdf = 255 * cdf / cdf[-1] 

im2 = interp(im.flatten(), bins, cdf)
im2.reshape(im.shape)

scipy.misc.toimage(img2, cmin=0, cmax=255).save("tmp.png")

Regardons ce code d’un peu plus près :

• On commence par l’ouverture d’image, ici rien n’a changé.
• On calcule ensuite l’histogramme de notre image. On récupère les deux variables découvertes au paragraphe précédent. On précise bien à la fonction que l’on travaille sur une image avec 256 niveaux différents, représentés sur l’intervalle [0;255]
• On calcule ensuite la fonction de distribution cumulative. Cette fonction nous permet de savoir comment sont réparties nos valeurs de pixels sur l’échelle de la luminosité.
• On normalise ensuite ensuite la fonction de distribution pour que ces valeurs soient réparties entre 0 et 255 et non plus entre 0 et 1.
• On applique une fonction d’interpolation sur notre image. Cette fonction d’interpolation va modifier la distribution courante de nos pixels (cdf) pour la faire tendre vers une distribution linéaire (bins). Le but est que notre distribution approche le plus possible d’une distribution linéaire, qui est représenté par un histogramme plat.
• On redonne au tableau unidimensionnel obtenu la forme de notre image de départ.
• On enregistre le résultat

J’ai préparé une image "dégradée" pour qu’on puisse voir si cela fonctionne bien.

Et après

Regardons les histogrammes aussi pour voir si nous avons réussi.

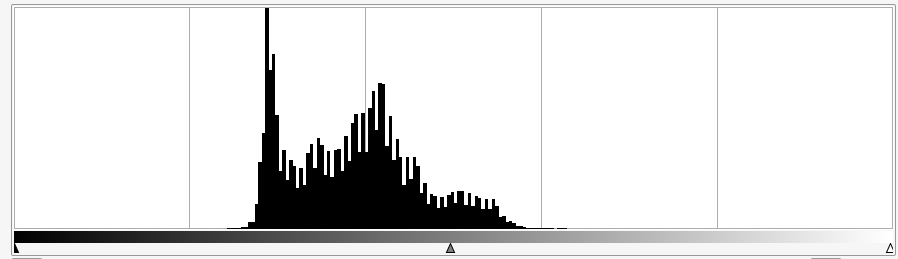
On peut constater qu’avant la modification l’histogramme est très compact et occupe un faible espace sur la largeur : l’image présente peu de valeurs différentes, elle est faiblement contrastée.

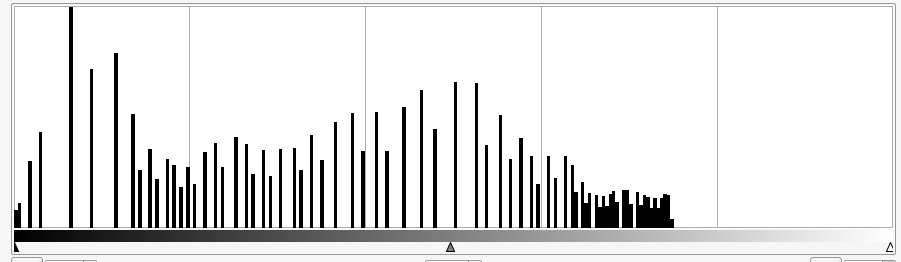
Après modification on obtient un histogramme qui occupe presque toute la largeur. Notez comment l’histogramme ne comporte que quelques pics, c’est typique de cet algorithme. Cela est dû au fait que dans l’image d’origine on travaille avec peu de valeurs différentes, on obtient donc peu de valeurs dans l’image résultat. Elles se retrouvent juste mieux réparties dans la largeur.

Voici pour comparaison l’histogramme de notre image avant dégradation. Pas mal non ?

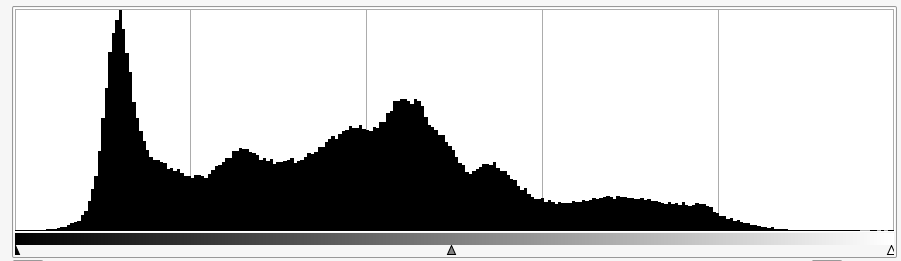
On peut constater que l’histogramme après l’opération et celui de l’image de base sont assez semblables. On a évidement perdu beaucoup d’informations au passage, mais les pics de valeurs se trouvent aux mêmes endroit et l’histogramme à la même forme générale.

Filtres

Les choses sérieuses commencent ! Le but de cette section est d’appliquer un filtre à une image. Un filtre est représenté par une matrice, généralement carrée et de dimensions impaire. On parle par exemple de filtre 3x3 ou 5x5, ce sont les dimensions les plus courantes. Pour appliquer un filtre à une image on effectue un produit terme à terme entre le filtre et une sous matrice de notre image, et on somme les éléments obtenus. Ce résultat devient la nouvelle valeur du pixel. La sous matrice est extraite de l’image sachant que la valeur au centre de la sous matrice correspond au pixel que l’on souhaiter traiter, le "pixel courant". On traite ainsi l’image pixel par pixel. Un petit schéma s’impose.

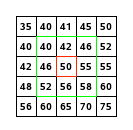
Le schéma marche bien quand on prend un pixel en plein centre de l’image. Mais c’est une autre paire de manche dans les coins ou en bordure de l’image.

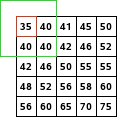
Certains pixels se retrouvent sans valeurs, impossible d’appliquer le filtre. Pour leur donner une valeur on utilise une stratégie de remplissage :

• La technique la plus naïve consiste à remplir avec des pixels blancs ou noir ou d’une valeur moyenne. Cette méthode est très rapide mais provoque souvent des défauts sur le bord de l’image.
• L’enroulement est aussi parfois une stratégie utilisée, cela consiste à procéder comme si l’image était enroulée autour d’elle même. Ainsi si on cherche à accéder à un pixel du bord supérieur qui n’existe pas, on utilise un pixel du bord inférieur de l’image. Cette méthode est très simple à mettre en oeuvre, mais donne des résultat variants en fonction du type d’image.
• On peut procéder par étirement ou par symétrie en recopiant les pixels de la bordure concernée. L’étirement provoque aussi de légers défauts sur les bordures (en fonction du filtre utilisé). La symétrie donne en général le meilleur ratio qualité / temps de calcul

Voyons quel filtre nous allons pouvoir appliquer. Comme beaucoup d’opérations en mathématique notre système de filtre possède un élément neutre, c’est-à-dire un élément qui ne va rien faire du tout (comme le 0 pour une somme). Dans notre cas le filtre neutre est le suivant, avec lui on peut vérifier que tout reste à l’identique

Pour l’appliquer à notre image on utilise le code suivant, sans oublier de rajouter dans vos imports from scipy import ndimage :

1
2

k = np.array([[0,0,1],[0,1,0],[0,0,0]])
im = ndimage.convolve(im, k)

On déclare simplement une matrice 3x3 appelée $k$ (pour kernel) et on applique la convolution entre notre image et le filtre. Voyons en détails comment cela fonctionne avec un bloc de pixels à traiter.

Pour rappel le résultat du filtre pour le pixel au centre du bloc à traiter est la somme des produits termes à termes de deux matrices, ce qui donne dans notre cas :

Notre pixel retrouve bien sa valeur initiale. Si on regarde la documentation de la fonction on voit qu’il est possible de spécifier la stratégie de remplissage pour les bords. Vous pouvez tester les différents modes pour essayer de trouver les défauts provoqués sur les bords. Je vous met ici un exemple de défaut réalisé avec le mode constant et une cval de 0.

Le but du filtrage est quand même de modifier notre image, alors regardons de suite un filtre permettant de flouter (filtre qui réalise une moyenne). Pour une taille de 3x3 le filtre est le suivant.

Le code a utilisé est le suivant :

1
2
3

k = np.array([[1,1,1],[1,1,1],[1,1,1]])
im = ndimage.convolve(im, k)
im = np.divide(im, 9)

Notez que j’applique une division par neuf après la convolution. J’aurais plus aussi écrire ces divisions dans la matrice $k$, mais la lecture en devient plus difficile. On peut aussi réaliser la division avant la convolution, peu importe. Le résultat obtenu est le suivant.

Déroulons ensemble un exemple sur un bloc à traiter constitué d’un pixel blanc au centre, entouré de pixels noirs:

L’intensité lumineuse de notre pixel central a diminuée. Si on appliquait le même calcul sur le reste du bloc (si la zone au alentour est noir) nous verrions que les pixels voisins sont eux devenus gris. Le principe est assez simple, le filtre réalise une moyenne entre les pixels avoisinants, ce qui "gomme les détails", c’est-à-dire qui supprime les informations donnant la sensation de netteté. Il est possible d’augmenter la taille du filtre pour un floutage plus fort. Plus la taille du filtre est grand (pour une même image) plus le temps de calcul est long. C’est dû au nombre d’opérations élémentaires (sommes, multiplications, etc.) qui explose avec les filtres les plus grands.

Il existe plein d’autres filtres de convolution mais à l’inverse de l’élément neutre et du filtre moyenneur difficile de les deviner. Je vais vous montrer quelques filtres amusants et courants en traitement d’image.

Renforcement des contours

Grâce à ce filtre on ajoute à notre image un renforcement des zones contrastées (non unies). Le filtre ne touche pas aux aplats mais renforce les contours de l’image.

On peut s’intéresser au résultat du filtre dans deux zones de notre image :

• Dans une zone unie, un aplat : si on considère que tous les pixels de la zones ont environ la même valeur le résultat de la convolution sera le pixel d’origine non modifié. Soit une zone d’aplat dont les pixels ont pour valeur $x$, on aurait

On peut en conclure que dans une zone d’aplat ce filtre ne modifie pas la valeur des pixels. Dans une zone contrastée, avec un trait vertical plus clair, on aurait :

Dans une zone contrastée notre pixel se retrouve avec une valeur deux fois plus élevée que ça valeur initiale, en augmentant le contraste local cela donnera une sensation visuelle de netteté accrue.

Détection de contours

Dans le même esprit on peut réaliser une détection de contours avec une suppression des zones unies de l’image. Ce genre de filtre peut être intéressant pour de la détection d’objets, de personnes, de formes, etc.

On peut voir que le filtre va faire la différence entre la valeur du pixel courant (multiplié par 8) et les pixels environnants. Le résultat obtenu avec ce filtre est le suivant.

On peut aussi décider de détecter les bords dans une seule direction avec un filtre de ce type.

On peut tout de suite voir la différence dans le fonctionnement du filtre : celui-ci ne considère pas les pixels voisins dans le sens vertical du pixel à traiter. Une importance particulière est aussi donnée à la ligne courante par rapport aux pixels en diagonal. Ce filtre fait partie des filtres de Sobel.

Maintenant que nous avons un peu joué avec les filtres, regardons un peu leur fonctionnement de manière empirique. Intéressons-nous à la somme des coefficients d’un filtre. Pour le filtre neutre ou les filtres moyenneur cette somme est de 1. Coïncidence ? Je ne crois pas. En effet ces deux filtres ont un point en commun, ils ne modifient pas la composante continue de l’image. Autrement dit ils ne changent pas les zones d’aplats. On tire de cette remarque la règle suivante.

Et quand la somme n’est pas de zéro ? Et bien ça dépend mais vous pouvez aussi regarder les filtres précédemment et en déduire une autre règle. On constate en effet que quand la somme des coefficients est nulle on se retrouve avec une image majoritairement noire. C’est en fait car il y a eu suppression de la composante continue de l’image, c’est à dire de sa moyenne de luminosité.

C’est fini pour cette grosse section sur les filtres. Vous pouvez facilement en trouver des listes sur internet ou inventer les vôtres.
On se retrouve dans la conclusion pour quelques infos supplémentaires.

C’est tout pour ce tuto sur le traitement d’image. Pour rappel nous aurons vu les opérations suivantes :

• Ouvrir et charger un fichier
• Réaliser des opérations ponctuelles (ajout de valeur, modification du contraste, etc.)
• Réaliser des opérations sur l’ensemble de l’image (agrandissement, filtres, etc.).
• Enregistrer le fichier

Bien sûr, il ne s’agit là que d’une introduction au traitement d’images et pour chaque opération nous n’avons qu’une approche simple. Le traitement d’image c’est aussi savoir comment enchaîner ces opérations pour arriver à son but : améliorer le côté artistique d’une image, préparer une image à un traitement de reconnaissance de texte, etc.

Et la couleur dans tout ça ?

Vous aurez remarqué que durant tout ce tutoriel nous n’aurons travaillé que sur des images en nuances de gris (et parfois en noir et blanc ou en bichromie). Il est bien évidement possible de traiter les images en couleurs, mais il est courant de se concentrer sur la luminance pour les débutants. Toutes les opérations vues ici s’appliquent à une image couleur, il faut juste traiter différents canaux de données. L’information de couleur est utile dans certains cas comme par exemple la détection d’objets : détecter un panneau de signalisation sur une photo par exemple. Il faut néanmoins savoir que de nombreuses caméras (scientifiques ou de surveillance par exemple) fonctionnent en nuances de gris.

Pour aller plus loin

Si cette petite introduction au traitement d’images vous a plus je vous redirige vers les sujets suivants pour approfondir :

• Le format JPEG
• Les filtres de convolution dans le logiciel GIMP
• Un page web pour tester des filtres de manière interactive
• Fudamentals of image processing (en - PDF)