Répartitions des fréquences

Bonjour à tous,

Pourquoi la répartition des fréquences ne suit pas une courbe en cloche ?

En considérant un spectrogramme, on constate que le milieu de ce dernier est occupé par des IR mais que ces fréquences sont bien moins nombreuses que, par exemple, les rayons X.

Alors que normalement, le milieu d’une distribution est censé avoir le plus grand cardinal :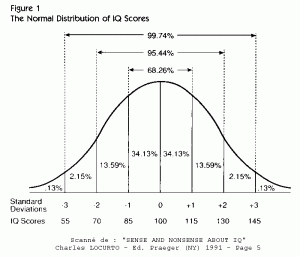

Alors il serait possible que ce soit juste un souci de classification, qui serait effectuée sans tenir compte des diverses propriétés de chaque fréquence. Mais bien entendu, les rayons X n’ont pas les mêmes propriétés que les autres fréquences, et cette classification a bel et bien été réalisée en fonction des propriétés des fréquences observées, non ?

Donc ma question devient (mais garde la même signification) : Pourquoi la répartition des propriétés des fréquences ne suit pas une courbe en cloche ?

Voilà voilà

Salut,

J’ai rien capté à ta question. De quelle courbe tu parles ?

Si je prends juste ce morceau de ta question qui est celui qui est le moins incompréhensible :

En considérant un spectrogramme, on constate que le milieu de ce dernier est occupé par des IR mais que ces fréquences sont bien moins nombreuses que, par exemple, les rayons X.

Tu veux dire que la plage des IR en fréquence est plus petite que celle des RX ? Si oui, il n’y a strictement rien de physique derrière, c’est juste une classification arbitraire. Il n’y a aucune différence physique entre un rayonnement IR et un rayonnement RX, le nom donnée aux différentes plages de fréquences vient juste de l’utilisation/contexte historique dans lesquels on observe ces rayonnements. Par ailleurs, les IR ne sont pas spécialement au milieu, il n’y a d’ailleurs pas de milieu dans ce spectre puisqu’il n’a pas de borne supérieure.

EDIT :

Alors que normalement, le milieu d’une distribution est censé avoir le plus grand cardinal

Une variable aléatoire n’a de manière générale aucune raison d’avoir une valeur moyenne qui coincide avec le maximum de densité de probabilité. C’est le cas pour les distributions gaussiennes qui reviennent souvent dans la nature, mais ce n’est pas une généralité (prends un jet de dé, la valeur moyenne du jet est de 3.5, mais la densité correspondante est nulle, tu ne feras jamais 3.5 en lançant un dé). Tu confonds par ailleurs deux choses qui n’ont rien à voir entre elles, la plage de fréquence d’un certain rayonnement n’a rien à voir avec une densité de probabilité d’une variable aléatoire…

Un peu comme adri1, je n’ai pas compris grand chose à la question.

Tu sembles dire que dans tout phénomène ’naturel’, on a une courbe en cloche (une courbe de gauss). Mais ce postulat est totalement faux.

Quand tu mesures un phénomène, si ce phénomène peut varier de -oo à +oo, alors ok, partir du principe que ce phénomène a toutes les chances de se simplifier via une courbe en cloche (une gaussienne), c’est possible.

Mais à partir du moment où tu mesures un phénomène qui ne peut prendre que des valeurs positives, alors déjà, tu es certain que la fameuse cloche de Gauss n’est plus adaptée. Si tu veux étudier des distributions de fréquence, tu peux éventuellement remplacer chaque fréquence f par g=ln(f). Ainsi g peut prendre des valeurs allant de -oo à +oo, et tu peux regarder si la courbe obtenue après ce changement de variable est une gaussienne.

Mais à partir du moment où tu mesures un phénomène qui ne peut prendre que des valeurs positives, alors déjà, tu es certain que la fameuse cloche de Gauss n’est plus adaptée.

Boarf, ça dépend de combien ta valeur moyenne est loin de 0 (la définition de "loin" dépendant de l’écart-type associé). Prendre une gaussienne pour la taille des hommes ou des femmes d’une population, ça passe. Ça te donne une probabilité non nulle d’avoir une taille négative ou plus grande que 10 m, dans les faits on s’en fout pas mal…

Les infrarouges (quelques fréquences) sont largement moins nombreux que les rayons X (des milliards de milliards de fréquences).

Donc tu n’as pas de distribution uniforme…

Pourquoi la répartition des QIs, ton problème aurait été plus compréhensible avec une image le définissant.

Les infrarouges (quelques fréquences) sont largement moins nombreux que les rayons X (des milliards de milliards de fréquences).

Non mais ça, ça veut rien dire… Le cardinal des fréquences possibles dans ces deux domaines est le même, et c’est le même que le cardinal de $\mathbb R$.

Les IR, c’est en gros de 300 GHz à 400 THz, les RX de 30 PHz à 30 EHz. Les RX couvrent une plus grande gamme en linéaire (mais c’est kiff-kiff en échelle log…), mais encore une fois ça n’a aucune signification profonde, ce ne sont que des limites arbitraires.

Ahah malgré ma question pas claire, vous avez bien réussi à comprendre ce que je demandais, merci !

Par contre @adri1 : es-tu sûr que la classification des fréquences s’est faite indépendamment de leurs propriétés physiques ? Tu dis qu’elles ont toutes les mêmes caractéristiques mais d’après mon prof de réseau, les fréquences très basses sont utilisées par les sous-marins car elles se propagent un peu mieux dans l’eau que les autres. Il a donné un autre exemple : les fréquences ISM présentent des inconvénients dont les fréquences utilisées par les militaires sont dénuées. Il semblerait donc, à en croire les indications de mon prof, que les fréquences aient été placées dans des catégories en fonction de leurs propriétés physiques.

D’où effectivement ma question : pourquoi y a-t-il plus de fréquences se propageant "facilement" dans l’eau (i.e. : fréquences basses) que de fréquences appartenant au visible pour l’humain ? ===> Je pensais que la répartition gaussienne s’appliquerait.

Il y a, comme je l’ai dit, des contextes d’utilisation différents pour les différentes gammes de fréquence, mais il n’y a pas de différence fondamentale entre les différentes gammes. Le seul truc physique qu’il y a, c’est l’énergie transportée par photon qui est proportionnelle à la fréquence. Les RX sont plus énergétiques que les UV, mais la limite entre les deux est arbitraire. Les noms servent juste à pouvoir dire rapidement "on est dans cette gamme énergétique", mais il n’y a pas de raison particulière à la largeur et le nombre de domaines autre qu’historique.

Quant à la propagation dans l’eau, ça vient plus des fréquences que la flotte absorbe (donc les propriétés des molécules d’eaux et de leur liaisons) que de propriétés intrinsèques des rayonnements.

Ta dernière question sur le "pourquoi" n’a par ailleurs aucun sens. Il n’y a pas de raison qu’il ait plus ou moins de longueurs d’ondes visibles par l’oeil humain que de fréquences peu absorbées par l’eau. C’est aussi absurde comme question que de demander pourquoi il y a quatre pieds à une chaise, mais trois pattes à un transistor.

@adri1 Euh, les transistors n’ont pas que 3 pattes, tu oublies le substrat ! (OK, il est quasiment jamais accessible, mais techniquement il n’y a pas que 3 pattes)

C’est vraiment pas un point important du message…

Je vais reformuler le message de adri1 avec mes mots :

On classe les fréquences en fréquences visibles / fréquences audibles / etc etc en se basant sur les particularités de l’oeil et de l’oreille humaine. Si les hiboux faisaient la même classification, mais avec leurs critères à eux, il est probable que les seuils seraient différents. Et si les dauphins devaient classifier les fréquences, on aurait encore une autre classification.

Il y a les fréquences dans l’absolu, et il y a la classification des fréquences, faite par les humains.