Courbature de la terre

Bonjour,

Si la terre est une sphère, ainsi que souvent prétendu, je ne peux m’empêcher de me faire la réflexion suivante.

Si on se place en 2 dimensions, l’équation d’un cercle est $x^2+y^2=r^2$. Dans le cas de la terre, il semblerait que $r=$ 6371 km. Soit $a$ la hauteur d’une personne (disont 1.75 m), on a donc:

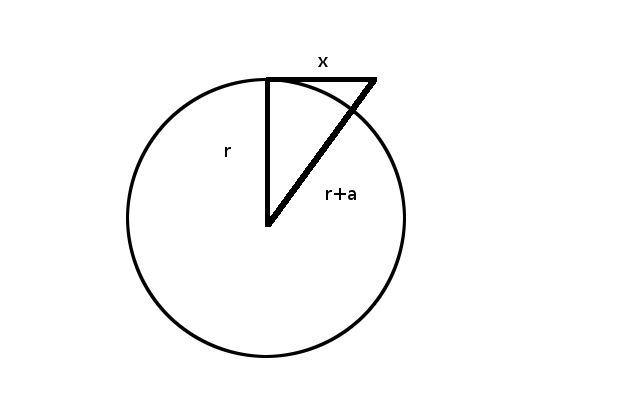
On a donc, selon pythagore, $(r+a)^2=x^2+r^2$, autrement dit, $x=\sqrt{a^2+2\,r\,a}$. Si on remplace avec les données que j’ai donné, on trouve 2,5 km environ (2524.08 m). Or sur un bateau, à la mer (oui, parce qu’il faut que ça soit plat), je peux encore apppercevoir la plage à 5 km de distance.

Alors … Ou est le problème? M’aurait-on menti?

Salut,

C’est rigolo, chez moi $\sqrt{2\times 6371\times 10^3 \times 1.75 + 1.75^2}\approx 4.7\mathrm{km}$, ça a l’air de mieux coller avec tes observations.

Par ailleurs, tu fais une hypothèse foireuse lorsque tu pars du principe que la mer, c’est plat. Elle le serait au repos, mais la présence de courants fait que tu peux facilement gagner localement 1 mètre par rapport au niveau de la mer moyen (c’est le cas au niveau de l’arrivé du gulf stream par exemple). Ajoute à ça le fait que lorsque tu es sur ton bateau, tu es surélevé par rapport à l’eau, tu peux facilement multiplier ta taille par 2 et donc multiplier la distance maximale à laquelle tu peux voir la plage par $\sqrt{2}\approx 1.4$, ce qui nous mène à 8 km dans le cas présent.

PS: on dit courbure, pas courbature.

Tu t’es trompé dans ton application numérique. J’ai trouvé un lien traitant du même problème (distance de l’horizon), et ils annoncent un peu moins de 5 km. Et leur calcul est juste bien sûr.

Et je renforce ce que dit adr1. Dès que tu es un peu plus haut, tu vois beaucoup plus loin. Par exemple, il est possible de voir par beau temps la côte anglaise depuis les falaises du côté de Calais, à plus de 30 km.

Et je renforce ce que dit adr1. Dès que tu es un peu plus haut, tu vois beaucoup plus loin.

Attention, ce que je dis c’est qu’être un peu plus haut te permet de voir un tout petit peu plus loin. L’horizon est à une distance $x=\sqrt{2ra}$ (le $a^2$ sera toujours négligeable devant le $ra$ puisque $a\ll r$, à moins d’aller dans l’espace). Si tu multiplies ta hauteur par un facteur $b$, tu ne multiplies la distance de l’horizon que par un facteur $\sqrt{b}$.

Oui. La Terre est en fait un disque reposant sur quatre éléphants, eux-même disposés sur une tortue géante.

Par exemple, il est possible de voir par beaucoup temps la côte anglaise depuis les falaises du côté de Calais, à plus de 30 km.

Et en jouant un peu avec la réfraction atmosphérique, on peut voir bien plus loin : À l’oeil nu, on peut voir la Corse depuis la France, les pyrénées depuis Marseille, et — avec un téléscope — certains on déjà vu les alpes depuis les pyrénées (443 Km, actuel record du monde).

C’est rigolo, chez moi $\sqrt{2\times 6371\times 10^3 \times 1.75 + 1.75^2}\approx 4.7\mathrm{km}$, ça a l’air de mieux coller avec tes observations.

En effet. J’ai dû oublier la multiplication par 2.

Par ailleurs, tu fais une hypothèse foireuse lorsque tu pars du principe que la mer, c’est plat. Elle le serait au repos, mais la présence de courants fait que tu peux facilement gagner localement 1 mètre par rapport au niveau de la mer moyen (c’est le cas au niveau de l’arrivé du gulf stream par exemple). Ajoute à ça le fait que lorsque tu es sur ton bateau, tu es surélevé par rapport à l’eau, tu peux facilement multiplier ta taille par 2 et donc multiplier la distance maximale à laquelle tu peux voir la plage par $\sqrt{2}\approx 1.4$, ce qui nous mène à 8 km dans le cas présent.

… Même si c’était la méditerannée, en l’occurence ?

Je crois pas, non.

Par exemple, il est possible de voir par beaucoup temps la côte anglaise depuis les falaises du côté de Calais, à plus de 30 km.

Faut voir d’où, mais ça peut se jouer (voir expliquation d’Adr1).

Vous êtes bien conscient d’invoquer un phénomène physique très complexe (et hypothétique) pour expliquer quelque chose qui peut s’expliquer plus simplement, non ? Et en plus, là, on a la preuve en photo.

Désolé mais ceci est une légende, il n’a jamais fait (assez) beau à Calais pour pouvoir vérifier cette affirmation (oui cette intervention était utile)

Quand tu es sur un tout petit bateau, disons que tes yeux sont à 2 mètres au-dessus du niveau de la mer. Tu regardes vers la plage. Disons pour simplifier que la plage est également à 2 mètres au-dessus du niveau de la mer (le début de la plage est au niveau de la mer, mais la partie que tu vois en premier est un peu sur-élevée). Le schéma que tu as fait au début est donc incomplet.

Tu as dessiné un triangle rectangle, mais en fait, il faut dessiner 2 triangles rectangles. La distance bateau plage est le double de ce que tu as dessiné.

Le regard part d’un point à 2mètres au dessus de la mer. Il se dirige vers l’horizon, la droite en question est tangente à la surface de la mer. Et la droite en question se prolonge, et au-delà du point de tangence, se trouve le point visé.

Et en plus, il y a les questions de réfraction de la lumière, non négligeables dans un tel environnement. La réfraction est complexe, mais pas hypothétique du tout.

PS : En fait, au début, je voulais réagir sur le mot "courbature" qui m’a beaucoup amusé, et j’ai failli oublié de le mentionner.

Une petite recherche wikipédia confirme pourtant.

Vous êtes bien conscient d’invoquer un phénomène physique très complexe (et hypothétique) pour expliquer quelque chose qui peut s’expliquer plus simplement, non ? Et en plus, là, on a la preuve en photo.

Peux-tu détailler ? J’ai peur des courbatures au cerveau.

Juste pour être sûr, quand tu dis "explication plus simple", tu parles de l’explication "la Terre est en fait plate" ? Si c’est le cas, il y aurait le problème inverse, c’est-à-dire que dans le cas général on ne peut plus voir la cote au-delà de 5 km (8km si on prend en compte le surélèvement dont parle @dri1). Si la Terre est plate, il n’y a aucune raison que la cote disparaisse au-delà de cette distance.

(Et je ne parle même pas du fait qu’on voit d’abord le sommet d’un phare à l’horizon avant d’en voir la base, ou des innombrables autres arguments immédiats qui réfutent la possibilité d’une Terre plate.)

… Même si c’était la méditerannée, en l’occurence ?

Apparemment le niveau de la Méditerranée varie de 30 cm autour de l’ellipsoïde de référence. Je ne saurais pas dire si c’est grâce aux courants, à la forme locale du géoïde, ou les deux. Dans tous les cas, c’est pas grand chose, la hauteur de ton bateau sera probablement plus importante.

Par exemple, il est possible de voir par beaucoup temps la côte anglaise depuis les falaises du côté de Calais, à plus de 30 km.

Faut voir d’où, mais ça peut se jouer (voir expliquation d’Adr1).

Si on ne s’occupe pas d’avoir les bonnes conditions météo, avoir l’horizon à $x=30$ km demande d’être à une hauteur de $a \approx \dfrac{x^2}{2r}\approx 70\mathrm{m}$. C’est bien le bon ordre de grandeur de hauteur des falaises de Calais.

Sinon, il y a un truc qui me désole un peu sur ce sujet, c’est le nombre de personnes qui jugent intelligent de troller/provoquer l’OP juste parce qu’il pose une question reliée à la courbure de la Terre qui ne lui donnait pas la bonne distance d’horizon. Il y a deux options : l’OP est sceptique sur le caractère sphérique de la Terre, se foutre de sa gueule au lieu de répondre sérieusement va pas aider à épancher son scepticisme (ni celui de potentiels futurs lecteurs); l’autre option est qu’il est ici pour troller, répondre comme vous le faîtes lui donne ce qu’il attend.