Bonjour!
J’ai dû demander à quelqu’un de plutôt calé en stats (enfin, du moins bien plus que moi) pour effectuer une régression non-linéaire sur des données que j’ai généré. Il m’a aussi mis des intervalles de confiance (d’après ce que j’ai compris ce sont des IC à 95%). Le résultat graphique le voilà:
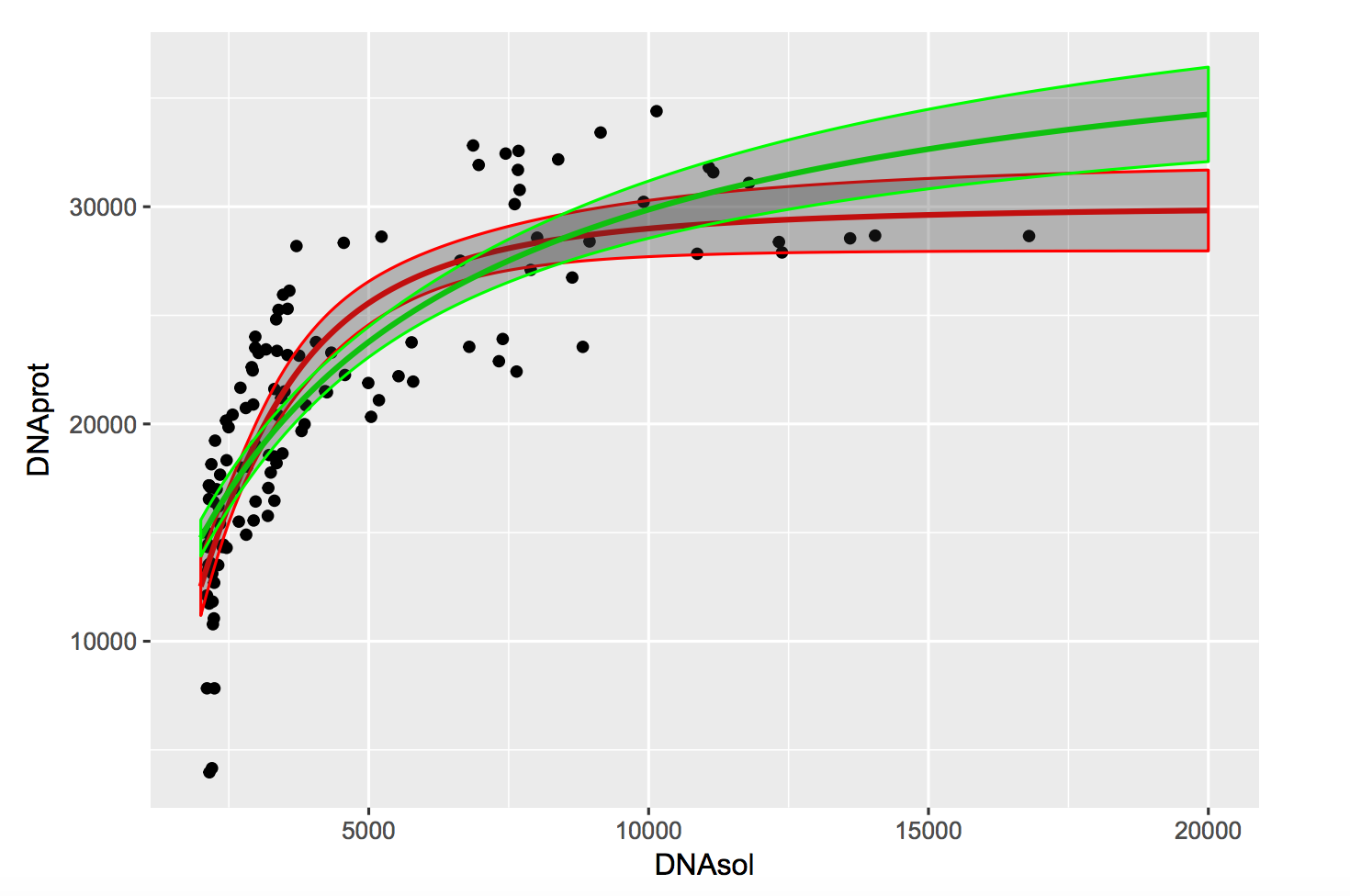
Y a deux courbes avec deux IC (apparemment à 95%) car ce sont deux modèles différents pour comparer lequel était le meilleur (rouge bien mieux).
Une question que je me demande c’est: pourquoi dans les deux cas des régressions les intervalles de confiances ne contiennent pas 95% des données (les points, ou alors je vois mal…) ? Peut-être que ça ne doit pas être le cas, je sais pas…  Pour info, ça a été fait avec des fonctions en R.
Pour info, ça a été fait avec des fonctions en R.
Si vous avez des idées, merci de partager vos connaissances là-dessus 

