Mathématiquement, faut pas oublier que tout ce fatras, c’est les "solutions de la résolution de l’équation de Schrödinger non-relativiste et indépendante du temps". Voilà voilà voilà, bonne soirée …
Bon, sérieusement. Ce que je ne sais pas, c’est ce que représente l’axe des y. Parce que soit c’est $\Psi$ (c’est à mon avis le cas vu que t’as du négatif), soit c’est $|\Psi|^2$, et ça signifie pas la même chose. Qu’entends tu part "probabilité", et qu’est ce qui te fais dire que c’est "multiplié par $r^2$" ?
Bon, en attendant, je suis obligé de revenir avec ma solution de l’équation de Shroedinger: ça représente la probabilité de trouver l’électron à une distance $r$ du noyau. Ton graphe pour $n=1; l=0$ dit exactement ça: l’électron d’une orbitale atomique $1s$ a plus de chance d’être trouvé proche qu’éloigné du noyau.
Autre question, mais pourquoi diable une 2s est aussi différente qu’une 1s ?
Parce que c’est pas la même couche électronique (= pas le même nombre quantique $n$). En gros, si tu superpose tes deux graphes, tu te rend compte que ça colle plus ou moins avec ce que tu sais déjà du modèle de Rutherford, c’est à dire que les électrons sont sur des "orbites" plus ou moins éloignés du noyaux. Là, tu "vois" que ton électron à une plus forte probabilité de ce trouver éloigné du noyau comparativement avec la $1s$.
Finalement, je me demandais pourquoi est-ce qu’on représente simplement la partie radiale R et pas la partie angulaire 
Parce que la partie angulaire est difficile à représenter (faut la voir dans les 3 dimensions de l’espace), et pas réellement intéressant. En fait, la partie angulaire, c’est ce que tu vois quand tu observe l’orbitale en 3 dimensions classique. C’est ce qui "impose" que la $p_z$ soit orienté selon l’axe des $z$, quoi 
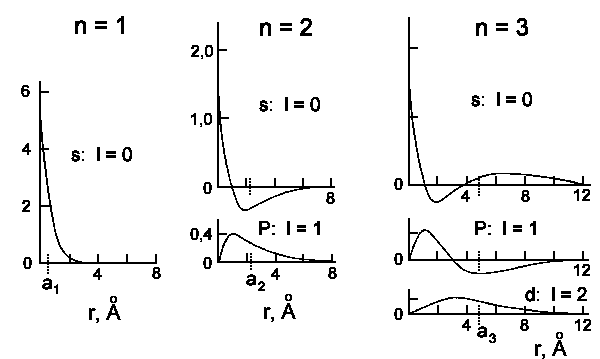




 Alors il y a une raison simple sur "pourquoi l’orbital est plus étendu si n est grand ?" : plus n est grand plus il y a d’énergie et donc plus l’électron peut s’éloigner du noyau (comme dans le cas classique). Après pourquoi la géométrie est si différente il y a peut être une interprétation physique … mais je ne sais pas trop.
Alors il y a une raison simple sur "pourquoi l’orbital est plus étendu si n est grand ?" : plus n est grand plus il y a d’énergie et donc plus l’électron peut s’éloigner du noyau (comme dans le cas classique). Après pourquoi la géométrie est si différente il y a peut être une interprétation physique … mais je ne sais pas trop.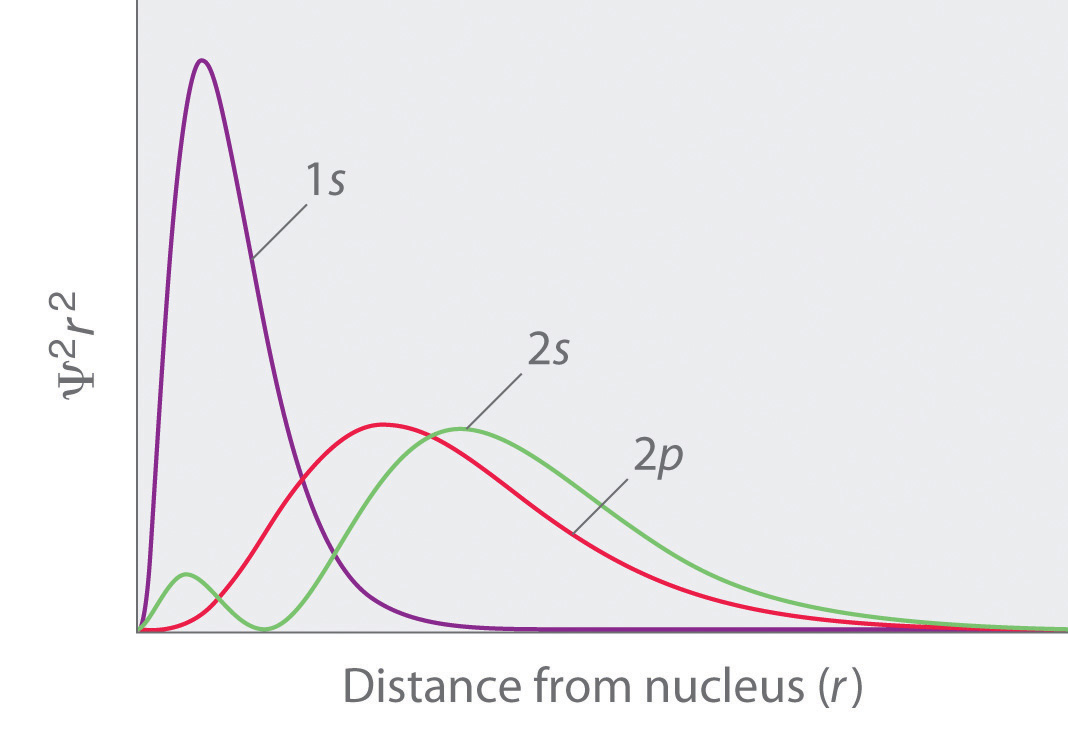

 #FinDuHS
#FinDuHS