Bonjour à tous,
J’ai un exercice sur la molécule d’ammoniac NH3. On nous dit que le potentiel peut-être approché par le schéma ci-dessous:
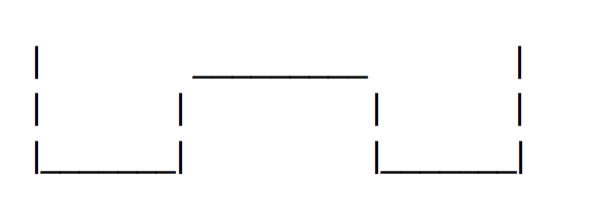
Je suppose que le double puit vient du fait que l’azote a ce fameux effet parapluie.
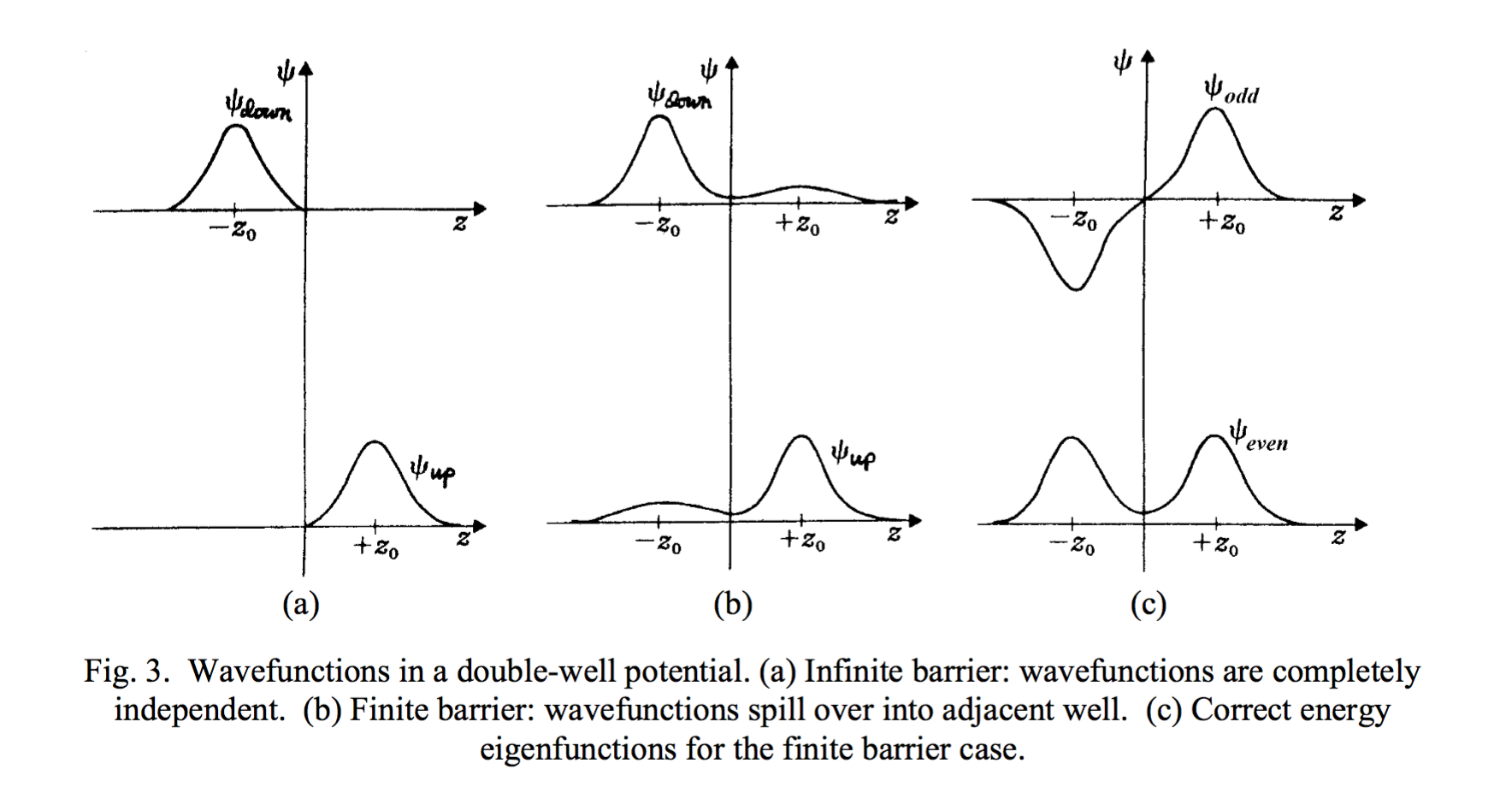
Je dois dessiner la fonction d’onde du niveau d’énergie le plus bas en justifiant. Déjà là, je bloque. Je dirais que une sinusoïde ayant un un minimum dans la partie A, un maximum au milieu de B et un minimum au milieu de C (se référer au schéma ci-dessous). Je suis pas du tout sûr (jamais eu de molécule aussi complexe en quantique et ça me perturbe  ).
).
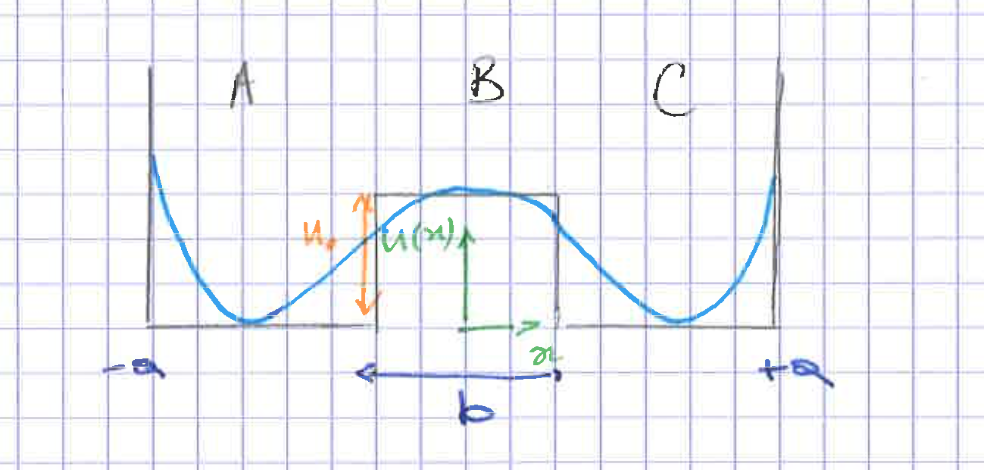
Puis, je dois résoudre analytique le problème. Je suppose qu’il suffit de décomposer le problème en trois régions A, B et C (ou dois-je aussi prendre l’extérieur de la "boîte" ?) Il s’agit simplement de l’équation de Schrödinger indépendante du temps: $ - \frac{{{\hbar ^2}}}{{2\mu }}\frac{{{d^2}\psi (x)}}{{d{x^2}}} + U(x)\psi (x) = E\psi (x)$ avec $U(x)$ nul en A et C et de valeur de la hauteur de la barrière et B. Après, on résous en faisant attention aux conditions de bords et on trouvera - je suppose - des fonctions sinusoïdales et exponentielles.
Ensuite, il me demande de donner la méthode pour résoudre avec une perturbation ce problème. Quelle perturbation vous pensez (il précise rien mais il faut bien un champ magnétique ou électrique pour qu’il y ait perturbation ?) ? Expliquer comment on ferait avec le principe variationnel en choisissant une bonne fonction de départ (trial function) et dire quelle méthode devrait être plus efficace. Je suppose qu’on peut choisir une combinaison linéaire de 2 ou 3 cosinus/sinus 
Par curiosité, est-ce qu’on aurait de l’effet tunnel ici ? Il précise pas si à l’extérieur les potentiels sont infinis.
Merci d’avance!