Salut, J’ai besoin d’aide car là je bloque vraiment..
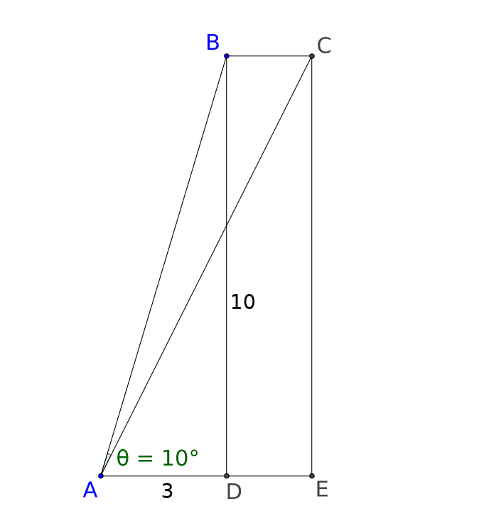
J’ai besoin de calculer l’angle en bleu en fonction de θ.
Pour cela, il me faut calculer la distance en bleu et ensuite considérer le triangle rectangle. Pour info, les 2 traits en bleu sont les mêmes (ils sont égaux).
Donc pour ma part, j’ai calculé la distance en jaune grâce au triangle rectangle à droite. Il me faudrait maintenant la distance en bleu. Elle me permettrait d’avoir la distance en rose et par conséquent, d’avoir l’angle en bleu qui dépend de θ. Mais pas moyen de trouver la distance en bleue 
De l’aide ?
+0
-0



 J’obtiens la moitié à vrai dire.
J’obtiens la moitié à vrai dire.