Bonjour à tous,
J’ai une question qui me trotte dans la tête depuis que j’ai refait des exercices sur la Chimie de Coordination. En voulant aller plus loin j’ai vue une grosse contradiction entre mes cours et internet.
- $X$ nombre d’élèctrons dans les 3 orbitales $t_{2g}$
- $Y$ nombre d’élèctrons dans les 3 orbitales $e_g$
- $n$ nombre d’élèctrons apparié
- $\Delta_0$ energie d’éclatement du champ cristallin
- $P$ energie d’appariement
Mon soucis se situe autour de $n$ je ne sais pas comment le calculer.
Je ne sais pas si $n$ prend en compte TOUT LES DNL, même avant appariement en bas spin, ou seulement les DNL créer par des ligands en champs fort.
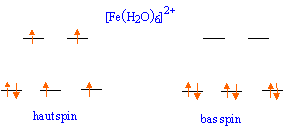
Par exemple ici, je compte :
- $n = 0$ pour le premier cas et $n = 2$ pour le deuxième ?
- $n = 1$ pour le premier cas et $n = 3$ pour le deuxième ?
Merci pour le temps de lecture accordé les copains
+0
-0

