Mécanique des fluides: fontaine

Le problème exposé dans ce sujet a été résolu.

Bonjour,

J’ai du mal à avoir comment résoudre ce problème.

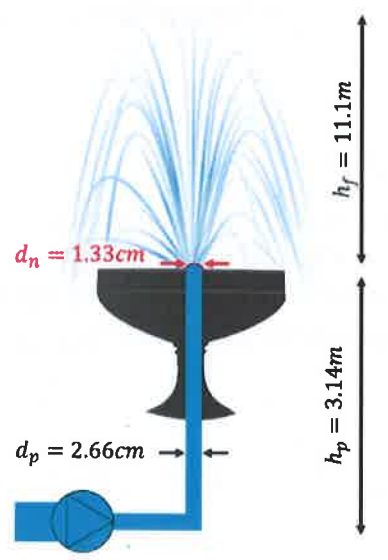
Une fontaine conçue pour pulvériser une colonne d’eau à 11,1 m dans l’air possède un embout 1.33 cm de diamètre au niveau du sol. La pompe à eau est à 3,14 m sous le sol. Le tuyau à la buse a un diamètre de 2,66 cm. Trouver la pression de la pompe nécessaire si la fontaine doit fonctionner comme prévu. (Supposons un écoulement laminaire non visqueux)

Fontaine

Je pensais partir sur l’équation de Bernoulli avec mon repère centré au sous-sol au niveau de la pompe.

$${P_{pump}} + \frac{1}{2}{\rho _w}v_1^2 = {P_{atm}} + {\rho _w}g{h_p} + \frac{1}{2}{\rho _w}v_2^2$$

La vitesse à la sortie, $v_2$, peut être trouvée avec Torricelli ${v_2} = \sqrt {2g{h_p}} $. Je pense ne pas avoir assez d’informations pour calculer $v_1$… Sauf si je peux appliquer le théorème de continuité (mais je suis pas certain vu la géométrie du problème). De plus, j’aurai pas $h_f$ ce qui est étrange.

Merci d’avance.

+0 -0

L’expression de la vitesse $v_{2}$ n’est pas correcte, pour déterminer $v_{2}$, il faut que tu ré-écrives à nouveau l’équation de bernouilli entre la sortie et le sommet de la colonne d’eau (l’eau y a alors une vitesse nulle, étant donné qu’il s’agit du sommet de la colonne). On obtient alors :

$P_{atm}+\frac{1}{2}\rho_{w}v_{2}^{2}+\rho_{w} g h_{p}=P_{atm}+\rho_{w}g(h_{p}+h_{f})$

Ce qui nous permet alors de trouver

$v_{2}=\sqrt{2gh_{f}}$

Ensuite les vitesses $v_{1}$ et $v_{2}$ sont liées par la conservation du volume, j’ai alors $v_{1}d_{p}^{2}=v_{2}d_{n}^{2}$.

En injectant les deux résultats précédents dans l’équation que tu avais initialement on obtient alors

$P_{pompe}=P_{atm}+\rho_{w}*g*(h_{p}+h_{f}(1-(\frac{d_{n}}{d_{p}})^{4}))$

+0 -0
Connectez-vous pour pouvoir poster un message.
Connexion

Pas encore membre ?

Créez un compte en une minute pour profiter pleinement de toutes les fonctionnalités de Zeste de Savoir. Ici, tout est gratuit et sans publicité.
Créer un compte