Bonjour,
J’ai une question sur cet exercice n’ayant pas la correction. Un courant électrique $I$ de densité homogène va en direction $Ox$ et couvre tout l’axe (Infini). La largeur du ruban est L (très mince). Un électron se trouve à la distance d, très faible, par rapport à l’axe de symétrie du ruban. Le champ magnétique généré par le courant exerce une force attractive $F_z$. On sait que l’énergie cinétique de l’électron vaut $E_c$.
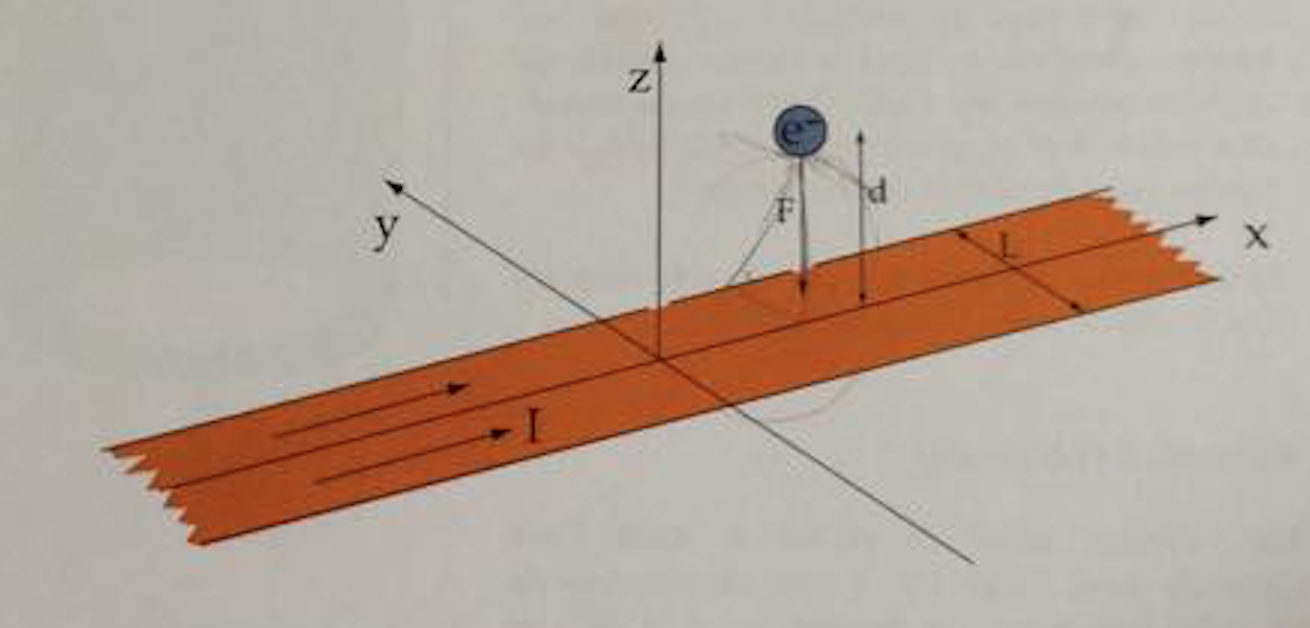
a) Calculez le champ magnétique à la position de l’électron (Module et composante).
J’ai pris le champ magnétique d’un fil infini. Par symétrie, je trouve que B est suivant l’axe -Oy.
$dB = \frac{{{\mu _0}Idy}}{{2\pi L\sqrt {{d^2} + {y^2}} }}dy$ (dI = I/L dy, densité de courant linéaire). Faut projeter (là je suis pas certain..): $d{B_y} = dB\cos \alpha = \frac{{{\mu _0}Iddy}}{{2\pi L({d^2} + {y^2})}}$ Je trouve après intégration, ${B_y} = \int\limits_0^L {\frac{{{\mu _0}Iddy}}{{2\pi L({d^2} + {y^2})}} = } \frac{{{\mu _0}I}}{{2\pi L}}{\mathop{\rm Arctan}\nolimits} (L/d)$.
b) Trouvez la vitesse de l’électron (module et composantes) et donnez toutes les composantes possibles de la vitesse …
Là, j’attends de voir si c’est bon au niveau du point a) mais je vois pas trop comment faire le b) (Avec la force de Laplace?). J’aurais peut être égalé Laplace et Lorentz..(?) Edit: En y réfléchissant, je me demande quelle est la nature de la trajectoire. $d$ étant beaucoup plus petit que $L/2$, ça ne peut pas être circulaire selon moi. Je vois plutôt une spirale!
