Bonjour,
Je ne comprends pas très bien les structures cristallines 3D compactes. J’ai bien compris la cubique simple et face centrées mais pas les compactes. J’arrive pas à trouver tellement d’informations dessus, particulièrement pour la cubique compacte. J’ai du mal à visualiser comment sont disposés les atomes et quel type de composés cristallisent là-dedans. J’ai entendu que c’était les plus optimal (74%) mais du coup c’est peut-être simplement théorique (?).
Si quelqu’un à une illustration, ça m’intéresse et aussi les nombres de coordinations 
Merci!
+0
-0

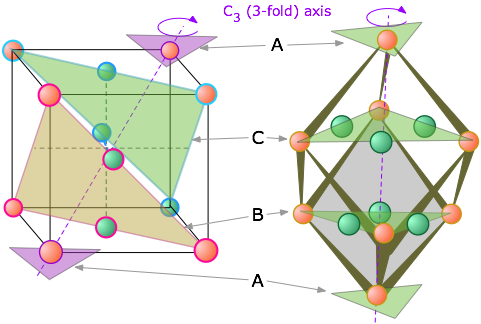
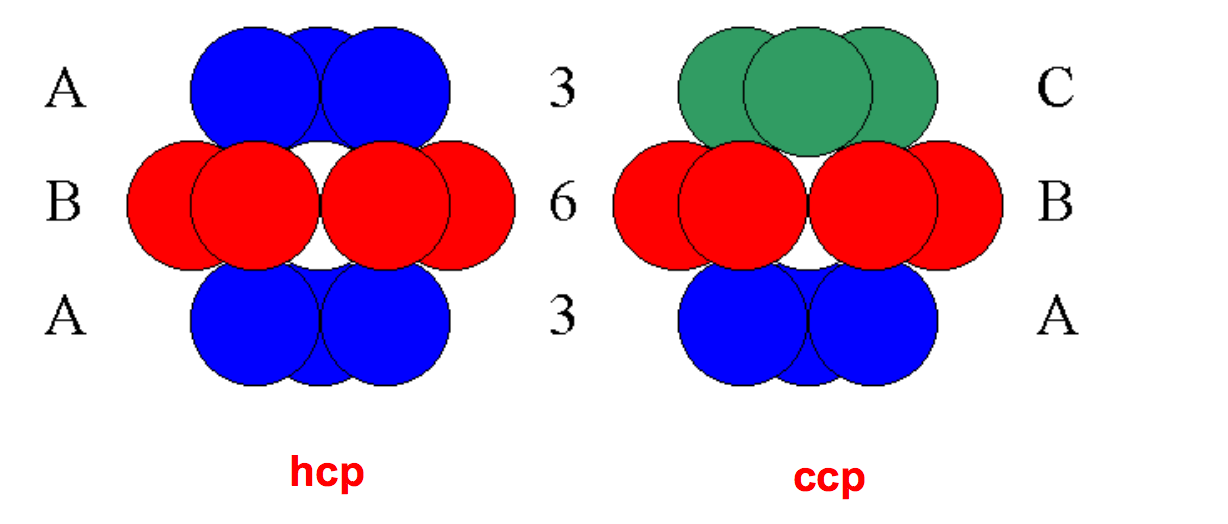 où hcp c’est l’hexagonale et l’autre la cubique. Je vois pas du tout avec cette image, la tienne est bien mieux
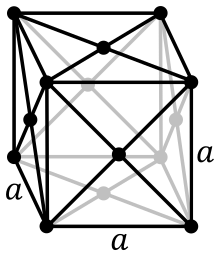
où hcp c’est l’hexagonale et l’autre la cubique. Je vois pas du tout avec cette image, la tienne est bien mieux  Si ça te dis quelque chose, je veux bien! Pour la maille hexagonale avec l’image ci-dessous j’aurais jamais deviné!
Si ça te dis quelque chose, je veux bien! Pour la maille hexagonale avec l’image ci-dessous j’aurais jamais deviné!