Bonjour à tous,
Je dois faire un algorithme/script sur Matlab pour tester la convergence de ces deux suites: % ${x_n} = a{x_{n - 1}} + b{x_{n - 2}}$ et ${y_n} = \frac{{a{y_{n - 1}} + b{y_{n - 2}}}}{{{y_{n - 1}}}}$ avec différents paramètres $a$ et $b$ et $x_{n-1}$ $x_{n-2}$ les deux premiers éléments de $x_n$ (idem pour y). On choisit de rentrer les coefficient $a$ et $b$ sous forme de vecteur coeff = [a, b] et les deux premières valeurs x = [ ${x_{n - 1}}$, ${x_{n - 2}}$ ]
Dans ma fonction testBoundaries, je regarde la convergence des suites (suivant la suite appelée). isBound =3 si j'ai un Sup et un Inf. isBound = 0 si elle diverge.
J'ai un problème avec une des suites que je teste, c'est la suiteY (cf. seriesFunY) avec les paramètres coeff=[0.5,-0.2] et x0=[1,0]. Elle me dit qu'elle converge alors qu'elle diverge grossièrement (clair suivant le plot effectué). Pour X ça fonctionne bien.
Voici les codes importants pour comprendre ce que je dis:
seriesFunY:
1 2 3 4 5 6 7 | function yn = seriesFunY(y2, y1, a, b)
switch nargin
case 4
yn = (a*y2 + b*y1)/y2; %scalar
case 2
yn = (y1(1)*y2(1)+y1(2)*y2(2))/y2(1);%vector
end
|
CalcSeries
1 2 3 4 5 6 7 8 9 10 | function x = calcSeries(seriesFun, coeff, x0, N)
x=zeros(1,N);
x(1)=x0(2);
x(2)=x0(1);
for i=3:N
x0=[x(i-1),x(i-2)];
x(i) = seriesFun(x0, coeff);
end
plot(x,'--')
end
|
-> Sert à calculer les N premiers termes de la suite.
callCalcSeries:
1 2 3 4 5 | x0=[1,0]; coeff=[0.5,-0.2]; N=100000; seriesFun=@seriesFunY; x=calcSeries(seriesFun,coeff,x0,N); |
(J'appelle la suite Y avec les paramètres comme dit avant)
TestBoudaries:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 | function [isBound,lowerbound,upperbound]= testBoundaries(seriesFun,p,errorThreshold,maxsteps)%hm2c
x(2)=p.a; %initialise x(1) et x(2)
x(1)=p.b;
i=2;
while i<maxsteps && abs(x(i)-x(i-1))>errorThreshold
x(i+1)=seriesFun(x(i),x(i-1),p.c,p.d);%call the function seriesFunX or Y
i=i+1;
end
switch nargout
case 1
if abs(x(i)-x(i-1))<errorThreshold && x(i)~=Inf && x(i)~=-Inf %Inf-Inf=0 and is < errorThreshold
isBound=3;
else if abs(x(i)-x(i-1))>errorThreshold%if it diverges not to +/- Inf the difference is > errorThreshold and it has no bound
isBound=0;
else if x(i)==Inf
isBound=1;%the case with no bound is already done so we verify only this condition to see if it has a lowerbound
else if x(i)==-Inf
isBound=2;%also only this condition has to be verified
end
end
end
end
case 3
if abs(x(i)-x(i-1))<errorThreshold && x(i)~=Inf && x(i)~=-Inf %Inf-Inf=0 and is < errorThreshold
isBound=3;
upperbound=max(x);
lowerbound=min(x);
else if abs(x(i)-x(i-1))>errorThreshold%if it diverges not to +/- Inf the difference is > errorThreshold and it has no bound
isBound=0;
upperbound=NaN;
lowerbound=NaN;
else if x(i)==Inf
isBound=1;%the case with no bound is already done so we verify only this condition to see if it has a lowerbound
upperbound=NaN;
lowerbound=min(x);
else if x(i)==-Inf
isBound=2;%also only this condition has to be verified
upperbound=max(x);
lowerbound=NaN;
end
end
end
end
end
|
Qui teste si elle est bornée. Le problème doit sûrement venir d'ici.
CallTestBoundaries: (pour appeler la fonction testBoundaries)
1 2 3 4 5 6 7 8 9 10 | x0=[1,0]; coeff=[0.5,-0.2]; p.a=x0(1);%initialize x(1),x(2) and the coeff in a structure p to have only one input p.b=x0(2); p.c=coeff(1); p.d=coeff(2); seriesFun=@seriesFunY; errorThreshold=10^-6; maxsteps=10^6; [isBound,lowerbound,upperbound]=testBoundaries(seriesFun,p,errorThreshold,maxsteps) |
J'aimerais aussi essayer de faire un cas pour des suites plus exotiques avec des cas isBound = 2 si la suite possède juste une borne supérieure mais pas inférieure (diverge en - infini et converge vers une certaine valeur en +infini par exemple). Je sais pas si c'est vraiment possible. Ca doit être beaucoup plus compliqué ?
Merci d'avance!


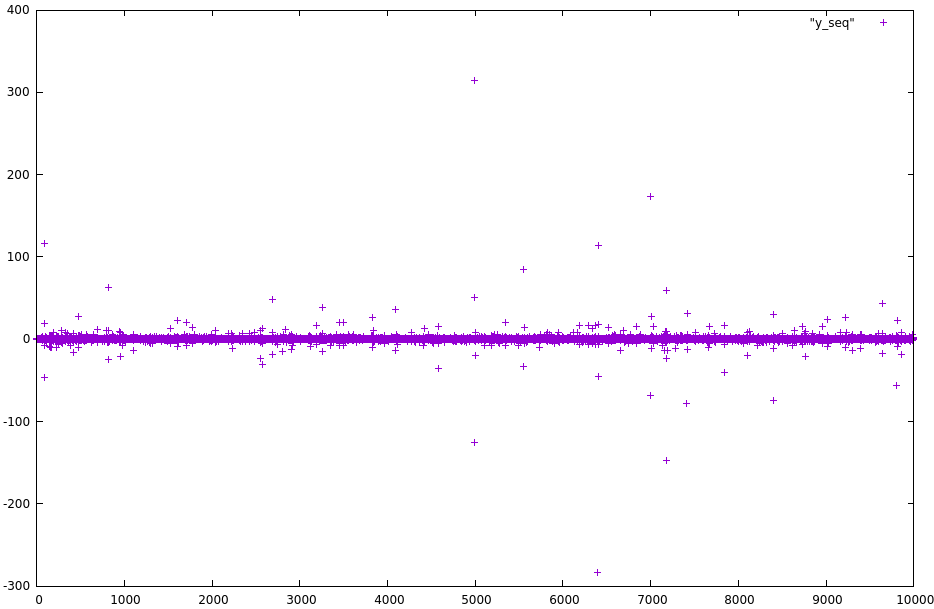
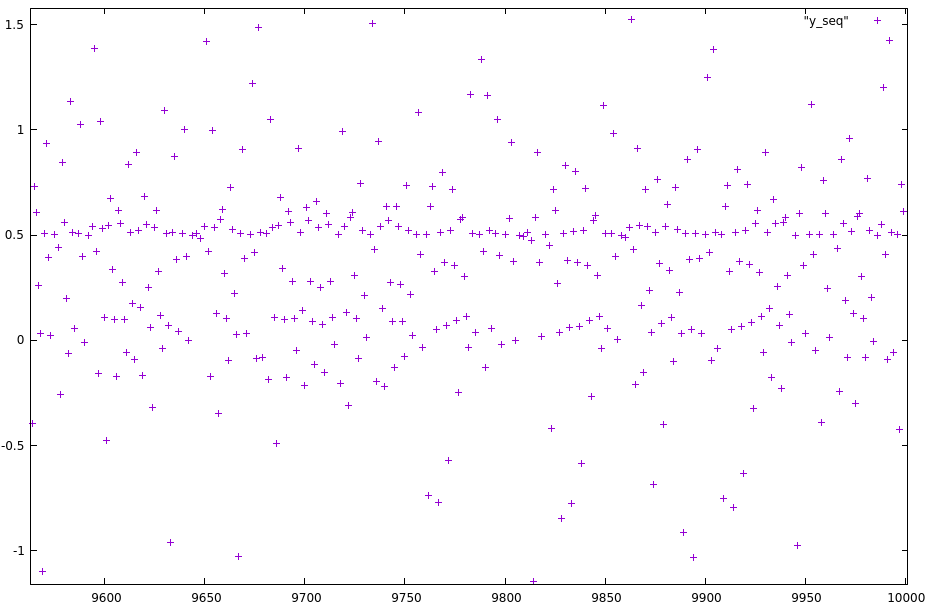
 Je suppose testBoudaries…
Je pensais mettre quelque chose comme ceci:
Je suppose testBoudaries…
Je pensais mettre quelque chose comme ceci: 