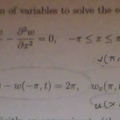Hello,
Je bloque sur un de mes DMs.
Utiliser la méthode de séparation des variables pour résoudre l’équation suivante
$$ \dfrac{\delta w}{\delta t} - \dfrac{\delta^2 w}{\delta x^2} = 0, \qquad -\pi \leq x \leq \pi $$ sujette aux conditions
$$ w(x, 0) = 0, \qquad w(\pi, t) - w(-\pi, t) = 2\pi, \qquad w_x(\pi, t) - w_x(-\pi, t) = 0 $$
Je ne vois pas du tout comment commencer. J'ai bien essaye
Soit $w(x, t) = X(x)T(t)$, en utilisant les conditions, on obtient :
- $w(x, 0) = X(x)T(0) = 0$
Donc $X(x) = 0$ ou $T(0) = 0$. Comme $X(x) = 0$ est la solution triviale de l’équation, nous allons prendre $T(0) = 0$.
- $w(\pi, t) - w(-\pi, t) = X(\pi)T(t) - X(-\pi)T(t) = T(t)[X(\pi) - X(-\pi)] = 2\pi$
Donc $T(t)$ doit être constante et ainsi $T(t) = 0$.
Dans tout les cas, la solution est $w(x, t) = 0$.
Ma conclusion est que $w$ n'est pas de la forme $X(x)T(t)$.
Quelqu’un pourrait m'indiquer la ou je me trompe ?
Merci d'avance.
+0
-0

 .
.