Bonjour,
Aujourd'hui, j'avais un peu de temps libre au boulot, du coup j'ai créé un petit programme marrant, basé sur des mathématiques de collège (voire de lycée avec le modulo). Pour ceux d'entre vous qui savent bien programmer (ce qui n'est pas mon cas) ou qui font des maths à un niveau supérieur, ca ne va pas être marrant. Pour les autres, on peut passer une demie-heure ensemble 
Je ne sais pas trop si j'aurais du poster sur le forum science ou programmation. Déplacez le sujet au besoin.
J'en vois certains venir, je vais présenter tout ca de manière très informelle. Je ne pense pas qu'il soit nécessaire de dire qu'on travaille dans R2, etc.
Le principe
Le principe sera de créer une image. Cette image sera constituée d'un cercle, et de segments dans ce cercle. Ces segments, reliants deux points du cercle, s'appellent des cordes. Ces cordes seront choisies à partir de deux paramètres : le nombre de points sur le cercle et un facteur multiplicatif. Vous verez que bien souvent, vous pourrez obtenir de "jolies" images.
Le nombre de points sur le cercle
Il va vous falloir les coordonnées de tous ces points. Le plus simple, c'est d'utiliser un cercle unité. Les points devront être équidistants. Ici, il faudra utiliser un peu de trigonométrie.
Le facteur multiplicatif
C'est ce facteur qui va définir les cordes à tracer. Si on numérote les points de 1 à N, et que l'on considère un point $i$, avec le facteur multiplicatif $f$, il faudra tracer une corde allant du point $i$ au point $i*f$
Une autre information ici. Si l'indice du point final est plus grand que N, c'est à dire qu'il n'y a aucun point avec cet indice, alors il vous faudra retrancher N jusqu'à obtenir un indice existant. Par exemple, si vous avez dix points sur le cercle, et que vous avez un indice multiplicatif qui vaut 3, il vous faudra tracer les cordes allant du point 1 au point 3, du point 2 au point 6, du point 3 au point 9.
La suivante devrait aller du point 4 au point 12, mais il n'y a pas de point 12. Du coup, on va aller au point 12-10=2. Suivant le même principe, il devrait y avoir une corde du point 7 au point 21, mais ce point n'existe pas. Il faudra donc retrancher 10. Mais le point 11 n'existe pas non plus. Du coup, il faut soustraire 10 une fois de plus, et tracer une corde aller du point 7 au point 1.
Cette opération s'appelle "prendre le modulo". On dira que 21 modulo 10 vaut 1. Quand vous allez programmer le code, écrire cette fonction pourrait être un bon exercice, mais elle sera très probablement déjà existante dans le langage que vous choisirez.
Le programme
Je ne suis absolument pas un expert en programmation, et ce que je propose est seulement une suggestion.
- Il faut lire les deux paramètres donnés en entrée
- Ensuite, il faut créer une liste/un tableau/peu importe où vous allez mettre les coordonnées de tous les points, après les avoir calculées
- Il vous faudra aussi créer une autre liste/un autre tableau ou vous allez mettre toutes les cordes à tracer.
- La dernière étape sera de tracer ces cordes
- Si vous le voulez, vous pouvez ajouter le cercle, pour rendre le tout plus joli.
Quelques exemples
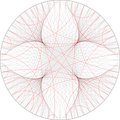
100 points avec un facteur 2
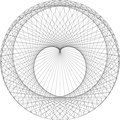
100 points avec un facteur 10
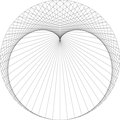
Et un bonus pour la Saint Valentin, 200 points avec un facteur 68
Le faire avec des arcs de cercle ?
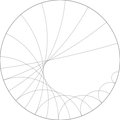
ρττ a eu l'ídée, quelques posts plus bas, de remplacer les cordes par des arcs de cercle. Il s'est imposé une condition, c'est que ces arcs de cercles devaient être perpendiculaires au cercle extérieur. Et les résultats sont aussi très jolis.
Pour y arriver, je vais vous l'expliquer pas à pas.
On va commencer par représenter le problème, sur un (beau) dessin.
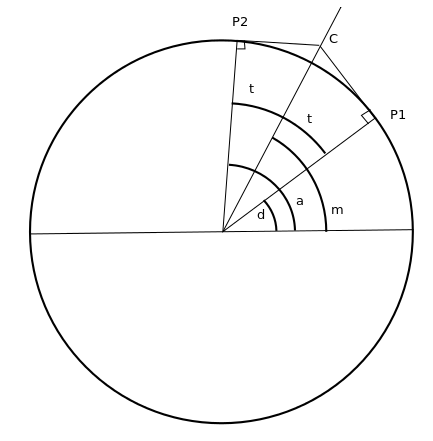
Que voit-on ici ? Tout d'abord, les deux angles correspondant aux points de départ (d) et d'arrivée (a). Ensuite, un angle, correspondant à l'angle de la bissectrice (m). Les angles t sont les angles (égaux) entre la bissectrice et les angles de départ et d'arrivée.
Ensuite, il y a trois points : C, le centre de l'arc de cercle que l'on veut tracer, et P1 et P2, les points entre lesquels il faut tracer l'arc de cercle.
Il va falloir utiliser la trigonométrie pour calculer :
- La distance entre C et le centre du cercle initial
- Le rayon de l'arc de cercle
En plus de ça, il vous faudra faire quelques opérations sur les angles pour déterminer entre quels angles tracer l'arc de cercle. Un dernier point sur lequel il faudra faire attention est de définir la bissectrice pour un angle saillant, et tracer l'arc de cercle pour un angle saillant aussi.
Et voici ce que ça peu donner (image prise d'un poste de ρττ un peu plus bas)
Conclusion
Si vous avez des questions, n'hésitez pas, et n'hésitez pas non plus à poster vos résultats !