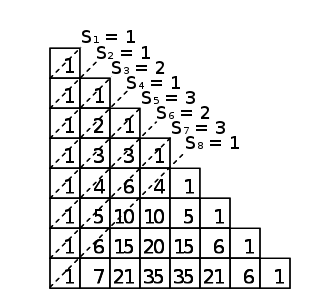
Je reprends pour la construction du triangle modulo 2.
Premièrement, on se place dans $\mathbb{Z}/p\mathbb{Z}$ avec $p$ premier et on fait la même construction que le triangle de Pascal. Ici, ce qui nous intéresse est $p=2$.
On compte les lignes du triangle en partant de $0$. Aucun $0$ ne peut apparaitre avant la ligne $p$ en utilisant la formule $\frac{(a+b)!}{a!b!}$ avec $0 \leq a+b < p$. À la ligne $p$, on va se retrouver avec quelque chose de la forme $1,0,\dots,0,1$ toujours en utilisant la même formule (avec $p+1$ nombres).
Ainsi, le triangle va se répéter deux fois jusqu'à la ligne $2p$. À cette ligne, on retrouvera la ligne $2$ avec des $0$ intercalés entre les nombres (chacun des deux triangles répliqués produira $1,0,\dots,0,1$, avec les deux $1$ du milieu qui se somment pour donner $2$). On va avoir un truc de la forme $1,0,\dots,0,2,0,\dots,0,1$. Les lignes suivantes sont encore le début du triangle répliqué (dont les coefficients sont multipliés par $1$ ou $2$), puis à la ligne $3p$ on se retrouve avec la ligne $3$ et des zéros intercalés. Ainsi de suite jusqu'à la ligne $p^2$ qui sera de la forme $1,0,\dots,0,1$. On réitère le raisonnement sur $2p^2$, jusqu'à $p^3$ et ainsi de suite.
On voit alors apparaitre une figure similaire au triangle de Sierpiński, avec des zones remplies de zéros (des triangles dont la pointe est en bas si on a dessiné le triangle de haut en bas). Les seuls zéros sont ceux qui sont dans ces zones.
On se place avec $p=2$. On nomme $u_n$ la somme comme tu l'as dit (et en fait on commence maintenant la numérotation des lignes à $1$). On considère la diagonale $2^n + k$ avec $0 \leq k \leq 2^n$. On coupe le triangle juste après la ligne $2^n$. La première partie de la diagonale est en-dessous de la ligne de découpe et est une copie de la diagonale $k$. La deuxième partie au-dessus ne se retrouve pas dans les termes précédents de $u$, mais on remarque que dans le cas particulier $p=2$, les triangles tronqués aux puissances de $2$ sont symétriques, et donc on retrouve en fait la diagonale $2^n - k$. Ainsi, on a $u_{2^n + k} = u_k + u_{2^n - k}$.