Dans bien des problèmes un peu complexe
complexes
de part leurs activités différentes elles peuvent
de par
avec a priori b2<a2
a priori
la configuration géographique des clients pourraient
pourrait
C'est pourquoi d'autres approches tentent de combler ces lacunes comme la complexité en moyenne, la complexité amortie ou la complexité lisse.
Plutôt : "C'est pourquoi d'autres approches, comme la complexité en moyenne, la complexité amortie ou la complexité lisse, tentent de combler ces lacunes."
les instances pathologiques sont souvent exclus
exclues
d'une mesure vis a vis d'une situation
vis-à-vis
et pour Π continue
continu
puisse obtenir le nombre exact d'opérations nécessaire
nécessaires
à la résolution de chacune des instances de l'ensemble S
C'est qui $S$ ? Le sous-ensemble des instances pratiques ?
perd tout intérêt en considérant que la mesure de probabilité
"en sachant" ?
Par exemple si l'on génère de manière aléatoire des tableaux à trier
Tu donnes un exemple artificiel, c'est ça ?
Comme le calcul exact est rendu impossible mais aussi inutile
Pourquoi inutile ?
on préférera une approche empirique
Je donnerais un exemple. Notamment, je ne comprends pas trop ce que signifie "en phase d'exploitation".
C'est bien sur impossible logistiquement parlant
sûr
pas tout à fait souhaitable à bien des égards et le premier serait que l'on cherche
pas tout à fait souhaitable à bien des égards, notamment parce que l'on cherche
plutôt une caractérisation a priori
a priori
et non pas à posteriori par l'efficacité
a posteriori
car moins sensible aux valeurs extrêmes
car elle est moins sensible aux valeurs extrêmes que la moyenne
Celui-ci est constituée d'une capacité
constitué
d'une capacité c mémoire
"de mémoire" ?
t<c
Je chipote, mais le nombre d'éléments n'est pas vraiment comparable à la mémoire: élément $\neq$ case mémoire.
Il en découle qu'on peut très bien avoir $t < c$ mais ne pas pouvoir ajouter d'élément dans le tableau. C'est le cas si $c - t < M$, où $M$ désigne la mémoire nécessaire pour stocker un élément.
Mais c'est vraiment pour chercher la petite bête. 
t<c,
Peut-être plutôt un " :".
c'est-à-dire asymptotiquement en O(1).
Je mettrais un point-virgule.
les éléments déjà présents sont copiés de l'ancien emplacement au nouveau
Le "au" me parait bizarre.
et que l'on agrandit le tableau que
n'agrandit
Or, d'une part, on peut retarder le besoin
Le "or" me semble inapproprié. Plutôt un "mais", parce que la suite explique qu'ajouter un élément au tableau peut se faire des fois en temps constant.
prendre en compte le fait que ce sont certaines opérations coûteuses qui permettent
Le "ce … qui" fait un peu lourd. Simplement : "prendre en compte le fait que certaines opérations coûteuses permettent".
La première politique consiste à simplement ajouter un à la capacité
La première politique consiste à simplement ajouter 1 à la capacité
Ou : incrémenter la capacité
La seconde politique se donne un peu plus de marge en donnant ajouter trois à la capacité
Pas très français. 
la taille de la capacité par deux chaque fois
Je ne suis pas sûr : "à chaque fois" ?
Il est évident que la première politique est optimale en terme de capacité:
Espace.
Il est évident que la première politique est optimale en terme de capacité: aucun espace mémoire n'est jamais inutilisé.
J'ai eu du mal à comprendre cette phrase avant de me rendre compte que les abscisses représentaient le nombre d'éléments dans le tableau. Tu devrais le préciser, même si ça parait évident.
Par contre, elle possède un coût moyen important puisque le pire des cas possibles.
Je pense qu'il manque un verbe après le "puisque".
à 2,8 mais augmente de facto la capacité moyenne
de facto
la capacité moyenne, passant de 5,5 à 6,6
laquelle passe de
le nombre moyen d'opération à 2,5 tout en augmenter légèrement la capacité moyenne
augmentant
si l'on refaisait le tracé sur une série plus longue d'insertions
Plutôt : "une série d'insertions plus longue".
les politiques additives sont peu scalables
J'expliquerais un peu ce terme. En note par exemple.
on n'utilise que ces dernières qui permettent un
dernières, puisqu'elles permettent
Cependant, leur but est d'apporter plus de robustesse à l'algorithme qui réagira mieux en limitant l'impact des opérations coûteuses sur la grande majorité des instances.
Cependant, leur but est d'apporter plus de robustesse à l'algorithme, qui réagira mieux puisque limitera l'impact des opérations coûteuses sur la grande majorité des instances.
maintenir une partition d'un ensemble en classes qui sont disjointes
Je ne comprends pas. C'est quoi une classe ? Que signifie "maintenir une partition" ?
Find, qui détermine la classe à laquelle appartient d'un élément en renvoyant son « représentant ».
; plutôt que .
Sans plus d'information
informations
l'implémentation est libre
Cela signifie qu'il en existe plusieurs ?
Sans plus d'information, l'implémentation est libre mais va entrainer des complexités différentes. C'est ainsi qu'une implémentation triviale utilisant des listes chaînées pour la représentation des classes aura une complexité amortie en O(m+nlog n) lorsque l'on effectue m appels successifs à Union puis Find sur n éléments.
Complexités différentes -> C'est ainsi -> un seul exemple de complexité.
Une solution est alors d'utiliser des arbres, qui
La virgule ne me semble pas nécessaire.
La fonction d'Ackermann est une fonction qui croit tellement vite que l'on peut considérer que son inverse vaut quatre quelle que soit la valeur de n.
C'est pas plutôt "inférieure à 4" ?
En effet, la fonction d'Ackermann au point (4,4)
Au point ? On ne lui donne pas des réels ?
Et si l'on renvoie le lecteur à la littérature pour plus de renseignement sur Union-Find
renseignements
Et si l'on renvoie le lecteur à la littérature pour plus de renseignement sur Union-Find et la démonstration de la complexité amortie associée, l'exemple est donné pour prendre conscience de l'écart entre ce que prédit la complexité dans le pire des cas et le comportement en pratique, représenté par la complexité amortie.
Je ne comprends pas la logique de la phrase.
la complexité dans le pire des cas reste la même ou augmente même
Plutôt : "reste la même, voire augmente".
Si la complexité en moyenne a été introduite pour palier certaines limitations
pallier à
contrairement aux études théoriques effectuées jusque là
jusque-là
sur un ensemble d'instances en les perturbants
perturbant
Cela permet de définir une espérance sur le nombre d'opérations, exprimée par
Peut-être pourrais-tu aérer en plaçant la phrase mathématique dans un nouveau paragraphe, au centre :
$$\forall x \in \mathbf R, x = x$$
Et là tu repars.
Alors la complexité lisse d'un algorithme sur Πn est donnée par
Dans la suite de la phrase, tu écris $\pi \in \Omega_{n}$. Ne serait-ce pas $\pi \in \Pi_{n}$ ?
Supposons que l'on puisse métriser l'espace
Le verbe "métriser" existe-t-il vraiment ?
d(Kσ1π,π)≤d(Kσ2π) presque sûrement
d(Kσ2π, π)
d(Pσπ,π) tend vers 0
P, c'est un opérateur de perturbation ?
De plus, je mettrais "$0$" plutôt que "0".
ce qui signifie alors que P est équivalent à l'identité : Kπ=π.
Il faut changer un P en K, ou un K en P.
on remarque que lorsque σ tend vers 0
$0$ ?
on retrouve la complexité dans le pire des cas
Là encore, il y a des $\Omega_{n}$.
Exemple de perturbation Considérons que
Il manque quelque chose. Un point, un retour à la ligne, un double-points…
s'il existe des constantes n0, σ0, c, k1 et k2 telles que pour tout n>n0 et 0≤σ≤σ0 alors
Le "alors" est étrange.
De plus, il semblerait que ce soit $K$ et non $P$ dans l'exposant.
Soit X une variable aléatoire réelle, presque surement positive
"sûrement". C'est la note sur l'inégalité de Markov.
qui possède une complexité lisse polynomiale, on obtient:
Espace.
De plus, juste après, il ne me semble pas que tu aies défini $\delta$.
À contrario, les problèmes utilisant des modèles mathématiques font souvent appels
A contrario
appel
Notons par ailleurs que l'algorithme du Simplexe
J'indiquerais entre parenthèses que tu fais référence au problème d'optimisation linéaire. D'ailleurs, tu n'as pas mis de majuscule à "simplexe" la première fois.
La complexité algorithmique asymptotique possèdent
possède
Prenons l'exemple d'un algorithme A et B, de complexité dans le pire des cas TA(n)=50x2+50x+5000
$x = n$ ?
La figure suivante présente le tracé des deux complexités exactes en fonction de la taille du problème
Même remarque que précédemment, sur le nom des courbes (f et g "au lieu de" A et B).
De plus, ce n'est pas vraiment la complexité, mais plutôt le nombre d'opérations, non ?
Si l'OGA indique que B est meilleur que B, la réalité n'est pas tout à fait aussi clair
Ca doit être cool d'être meilleur que soi-même. 
claire
l'algorithme A est meilleur que l'algorithme B
Euh, A c'est f, non ? Et f est au-dessus de g sur [0, 53]. Or les ordonnées représentent le nombre d'opérations. Donc B est meilleur que A, non ?
et que si je sais a priori que la majorité des instances
a priori
et des termes d'ordres inferieurs fortement pondérés
inférieurs
et augmentent le limite inférieure à partir de laquelle
la
Pire, même une étude précise, pourra être
Virgule en trop.
voire les structures de données elles-même
elles-mêmes
plus encore d'une implémentation d'un algorithme A à l'implémentation d'un algorithme B.
$A$ et $B$.
es facteurs qui propagent un peu plus cette incertitude sont bien évidemment l'abstraction matérielle, l'abstraction des implémentations de briques logicielles d'un niveau de granularité plus faible, comme des opérations sur les structures de données voire les structures de données elles-même dont on ne dispose pas toujours de l'implémentation, et évidemment, les optimisations matérielles et logicielles qui vont réarranger les opérations voire les remplacer par d'autres pour des gains généralement variables d'une implémentation à l'autre et plus encore d'une implémentation d'un algorithme A à l'implémentation d'un algorithme B.
La phrase est plutôt longue.
comme en témoigne l'exemple typique de l'algorithme du simplexe
"Simplexe" ?
On peut ensuite formuler le problème d'optimisation de manière très générale:
Espace.
Soit Ω, un espace dit des variables de décisions
décision ?
Soit f:Ω→Y, alors
La virgule fait bizarre. Je ferais : "Soit Ω, un espace dit des variables de décisions, X⊂Ω une partie de l'espace de décision souvent appelé espace admissible, Y un espace totalement ordonné appelé espace objectif, souvent R, et f:Ω→Y. Alors".
le problème de minimisation consiste à minimiser f sur X
Et si le minimum n'existe pas ?
L'ensemble X est obtenue par l'application de contraintes
obtenu
autrement dit le cercle de rayon l
Le disque.
Par ailleurs, la contrainte de la laisse attachée au pilier sur la position du chien est non linéaire.
Le "par ailleurs" me semble inadapté. Plutôt un "alors".
Un exemple de chose qu'on voudrait optimiser ici (i.e. un exemple de fonction $f$) ?
dont on cite quelques-unes des plus importante:
importantes :
Existence de solution :
Je le mettrais en gras.
La question peut faire sourire, mais il existe bien des problèmes où l'existence même d'une solution n'est pas facilement démontrable !
Tu pourrais au moins nous fournir une petite note là-dessus ! 
Un problème facile aura une preuve d'existence sans condition de solution
La phrase est bizarre. Plutôt : "Un problème facile aura une preuve d'existence de solution sans condition".
n'auront pas ces preuves d'existence ou alors, sous des conditions
n'auront pas ces preuves d'existence, ou alors sous des conditions
Problème multi-modal
En gras ?
plusieurs éléments de X donnent la valeur optimale pour f
minimale, non ? Ou alors il faut généraliser plus haut.
est obtenue autant par x=5 que
obtenu
un problème très difficile que seuls les méthodes
seules
l'existence de plusieurs modes est caractéristique de problèmes plus difficiles que les problèmes n'ayant qu'un mode
Mode = solution ? Ce qui est plus difficile, c'est de les trouver toutes, pas le simple fait qu'elles existent, si ?
problèmes multi-objectifs qui sont de facto multi-modaux
de facto
Pourquoi ? Je peux avoir plusieurs objectif et une unique solution les satisfaisant tous, non ? D'ailleurs, tu dis juste après : "il n'existe pas en général une solution".
pour ces problèmes sont une fois encore des techniques de types algorithmes génétiques
type
En général les méthodes adoptées pour résoudre ces problèmes sont des suites itératives xn dont on espère beaucoup de propriétés
Exemple ? Tu parles plus bas de la méthode de Newton, tu pourrais développer un peu. Notamment faire le lien avec le fait de vouloir minimiser une fonction. Concrètement, je ne vois pas ce qu'une suite vient faire là. J'ai ma petite idée, vu que je connais un peu la méthode de Newton, mais sans ça on ne voit pas le rapport avec $f$.
sont des suites itératives xn
$(x_{n})$ ?
converge-t-on nécessaire en un nombre fini d'étapes
nécessairement
la difficulté intrinsèque d'un problème était lié
liée
Durant des années on a pensé que la difficulté intrinsèque d'un problème était lié majoritairement à la caractéristique de linéarité ou non, les problèmes linéaires étant les problèmes faciles à résoudre.
Je reformulerais, parce que tu ne dis pas assez clairement que linéarité = simplicité. Plutôt : "La linéarité influe sur la difficulté intrinsèque d'un problème, les problèmes linéaires étant les problèmes faciles à résoudre, et durant des années on a pensé qu'elle constituait le facteur majoritaire. Cependant,".
en particulier voir Analyse fonctionnelle : théorie et applications de Haïm Brezis
Je pense qu'il faut formater le titre : guillemets, italique… je ne sais pas.
c'est-à-dire les contraintes s'appliquant à Ω dont il résulte
Je ne comprends pas le "dont il résulte". Tu parles de $X$ ? Je dirais plutôt "dont il est une partie".
Clarifions. L'exemple
Plutôt un ":" ?
L'exemple de programme d'optimisation linéaire permet d'obtenir un domaine X sous la forme d'un polytope, donc convexe par définition.
Pourquoi parler de convexité tout à coup ?
Dans l'exemple du chien et de la laisse, le domaine X est un cercle
Disque du coup, non ?
Ainsi, en étudiant la topologie du domaine X
Le "ainsi" ne se tient pas. Tu n'as fait que dire que les domaines pour la guerre et le chien étaient convexes, pas que cela rendait le problème plus simple.
couplée aux propriétés de f
Je rajouterais entre parenthèses : "telles que la linéarité".
la frontière serait plutôt l'optimisation convexe et l'optimisation non-convexe
On parle bien de la convexité de $X$, l'espace admissible ?
http://zestedesavoir.com/media/galleries/1822/ab4b7132-3148-427b-96cf-83dd9aeb6a6d.png.960x960_q85.png
Une petite légende pour dire qu'à gauche c'est convexe, mais pas à droite.
de résoudre les problèmes sur domaines
sur des domaines
comme l'existence d'une uniquement solution
telles que
unique
Pourquoi a-t-on l'existence et l'unicité ? Un disque ouvert (convexe) dans $\mathbf C$ n'a pas de maximum (en module), si ? Et un disque fermé en a plusieurs.
À contrario, les problèmes non convexes
A contrario
non-convexes ?
les problèmes non convexes sont fondamentalement difficiles
J'imagine que c'est pas évident d'expliquer pourquoi ?
qu'il n'existe pas d'algorithme qui peuvent
qui puisse
mais l'on ne dispose pas de preuve pour cela
mais que
Convexe versus non-convexe
versus
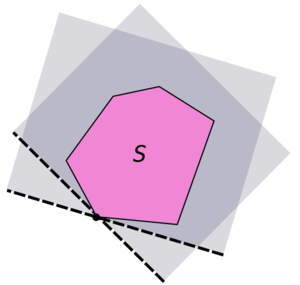
Soit E un espace normé, A et B deux convexes de E non vides et disjoints. On suppose A ouvert. Alors il existe un hyperplan fermé séparant A et B.
$E$, $A$… ?
En particulier, il est possible de séparer un singleton de la frontière d'un convexe avec le reste du convexe.
Je ne comprends pas trop le schéma là. Celui de droite est un contre-exemple ?
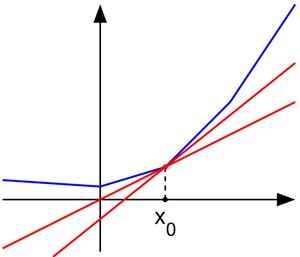
la notion d'hyperplan d'appui, et de fil en aiguille,
la notion d'hyperplan d'appui et, de fil en aiguille,
mais plutôt de donner quelques pistes de recherches
recherche
comme illustré sur la figure plus haut
Ca répond à ma question précédente du coup. Mais peut-être un peu tardivement. 
Je mettrais la partie droite du schéma sous cette phrase.
La figure suivante, représentant les hyperplans d'appui est posée comme une fleur…
En somme, on aurait plutôt :
Une version plus faible, ne supposant pas l'ouverture de A, permet d'obtenir le même résultat de séparation, mais par un hyperplan qui n'est pas nécessairement fermé. En particulier, il est possible de séparer un singleton de la frontière d'un convexe avec le reste du convexe.
Dès lors, on peut définir la notion d'hyperplan d'appui, et de fil en aiguille, définir le sous-différentiel en un point de la frontière du convexe comme l'ensemble des coefficients des pentes des hyperplans d'appui en ce point. Il ne s'agit pas d'entrer plus dans les détails, cet article concernant avant tout la complexité algorithmique, mais plutôt de donner quelques pistes de recherches pour le lecteur désireux d'en savoir plus.
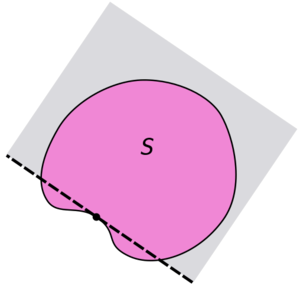
Au contraire, sur des espaces non-convexes, on peut trouver des points de la frontière pour lesquels le sous-différentiel n'existe pas, tout simplement car il n'existe pas d'hyperplan d'appui, comme illustré sur la figure suivante.
l'optimisation multi-objectif est particulièrement parlante
multi-objectifs
Dans un tel cas, la particularité est que l'on cherche l'ensemble des points de la frontière
Pourquoi juste sur la frontière ?
on cherche l'ensemble des points de la frontière du domaine qui réalise un équilibre de Pareto.
réalisent ? Je ne sais pas trop s'il est question de l'ensemble ou des points pris individuellement.
D'ailleurs, j'ignore ce qu'est un équilibre de Pareto.
Sur l'animation suivante, il s'agit de toute la frontière visible de l'espace objectif.
Je mettrais entre parenthèses "noir + couleur-que-je-ne-sais-pas-nommer". Ca me semble important comme précision parce qu'on ne comprend pas la suite si on ne voit pas ce qu'est exactement cette frontière.
http://zestedesavoir.com/media/galleries/1822/c3a699e5-ef9f-43ae-ac54-a4b7d69b03d2.gif
Il est écrit $F$ alors que tu as mis $f$ dans le texte.
Pourquoi $\omega_{1}$ ne va pas jusqu'à $1$ ?
Je ne comprends pas ce que sont les droites qui bougent.
Pourquoi $f_{1}$ et $f_{2}$ sont comprises entre $0$ et $1$ ?
dans lesquels les algorithmes habituels vont être piégés, comme c'est le cas de l'algorithme de Newton
Il faudrait vraiment que tu développes cet exemple (cf plus haut).
Comme nous l'avons vu, la notion pertinente pour caractériser la difficulté d'un problème est la notion de convexité
"une notion pertinente" plutôt, non ? Après, il ne me semble pas qu'on ait vu que la convexité impliquait la simplicité. Tu as donné un exemple illustrant le fait que la non-convexité impliquait la difficulté, mais tu n'as pas dit grand chose sur la convexité, c'est qui est normal, vu que tu as écrit : "Il ne s'agit pas d'entrer plus dans les détails, cet article concernant avant tout la complexité algorithmique, mais plutôt de donner quelques pistes de recherches pour le lecteur désireux d'en savoir plus.". Du coup, aurais-tu une source précise concernant le lien entre simplicité intrinsèque et convexité (une source sur les hyperplans d'appui j'imagine) ?
et non non pas celle de complexité des algorithmes pour le résoudre
Non, non, non, non, je ne veux pas t'oublier !
Cependant, comme suggéré, on peut tout de même raffiner en étudiant la nature du domaine de notre problème.
Je mettrais un truc du genre : "en étudiant les caratéristiques du domaine de notre problème, en sus de la convexité". Sinon, tu pourrais perdre certains lecteurs qui se demanderaient "mais c'est bien ce qu'on a fait juste avant, non ?".
Ainsi, si l'optimisation continue est
Pourquoi "ainsi" ? Plutôt "par exemple", non ?
si l'optimisation continue est en générale plus facile que l'optimisation combinatoire
Je ne connais personnellement pas ces termes.
On aimerait donc caractériser la robustesse d'un algorithme par rapport au problème qu'il résout
Je ne comprends pas le "donc".
De plus, ne cherche-t-on pas plutôt à caractériser la difficulté d'un problème, indépendamment des algorithmes le résolvant ? Il manque sûrement une petite phrase de transition.
Par varier on entend principalement donner des résultats empiriques temporels qui varient peu
C'est plutôt un truc du genre "Par varier peu on entend principalement donner des résultats empiriques temporels qui varient peu", non ? Mais c'est moche. Plutôt, tout simplement : "On entend principalement donner des résultats empiriques temporels qui varient peu".
autrement dit, une variance faible.
La phrase ne se tient pas. Il manque un "avec", non ?
Dans le cas de l'optimisation, on peut citer quelques exemples:
Espace.
Invariance par une transformation de la fonction objectif.
En gras ?
fonction objectif
Je ne crois pas que tu aies employé ce terme précédemment. J'imagine que c'est la fonction à minimiser ?
"fonction-objectif" ?
Plus la transformation préservant l'invariance à des propriétés
a
pour la transformation de la fonction objectif par une fonction strictement monotone
C'est un peu lourd, non ? Plutôt "pour la transformation par une fonction strictement monotone".
espace de recherche
Il s'agit bien de $X$ ici ?
On comprendra donc que ces propriétés d'invariance offertes par les algorithmes sont hautement désirables puisqu'elles permettent d'obtenir une généralisation des résultats empiriques à toutes les instances de la même classe par rapport à la relation d'invariance.
Il faudrait des exemples concrets (genre avec une guerre ou un chien) de transformation de la fonction objectif et de l'espace de recherche. Là, je ne vois pas du tout comment ça marche en pratique.
comme le montre le contre-exemple de l'algorithme du Simplexe
Toujours la question de la majuscule.
l'opérateur de perturbation est une transformation particulière, aléatoire notamment
Pourquoi "notamment" ?
on s'intéresse aux pires des cas obtenu par perturbation
"obtenus" ou "au pire"
et donc plus ou moins de manière corrélée à proposer peu de paramètres et des paramètres à domaine restreint
et donc plus ou moins, de manière corrélée, à proposer peu de paramètres et des paramètres à domaine restreint
On parle alors de métaheuristiques
Guillemets ? Ou italique.
Méta pour la variété des problèmes que ces méthodes
Guillemets autour de "Méta".
et heuristiques, car elles n'offrent, en général, pas de garantie
Guillemets autour de "heuristiques".
et se contente d'une solution approchée
contentent
auquel cas, les autres méthodes deviendraient obsolètes
La virgule est en trop je pense.
à moins d'exploiter l'information disponible au niveau d'un problème particulier, il n'existe pas de métaheuristique qui soit intrinsèquement meilleure qu'une autre
Mais du coup, une telle métaheuristique sera moins efficace sur les autres problèmes et s'éloignera un peu de son caractère de métaheuristique, non ?
http://zestedesavoir.com/media/galleries/1822/5d0b4109-e8b4-41a5-b9e2-9d4209696557.png.960x960_q85.png
Une légende me semble nécessaire. On comprend, mais quand même. 
Par ailleurs, les métaheuristiques étaient des méthodes approchées
Pourquoi l'imparfait ?
algorithme évolutionnaire possède souvent un nombre très importants
important
Un point plutôt qu'une virgule.
Dès lors, pour en tirer le meilleur sur une situation pratique, la phase d'exploitation, il faut calibrer l'algorithme, la phase de conception.
Je mettrais "la phase de …" entre parenthèses.
Et l'on se retrouve de fait avec un compromis à faire:
Espace.
des meilleurs paramètres versus la qualité des
versus
on obtient déjà un espace de configuration de taille
J'ai pas compris comment tu obtenais ce calcul.
pour rapidement trouver des paramètres de bonnes qualités
bonne qualité
La facilité à être optimiser provient surtout
optimisé
on parle de méthode en ligne
Italique ?
Dès lors, l'utilisateur final n'a plus à ce soucié de ce paramètre
se soucier
On ne peut pas en tirer beaucoup d'information
informations
On ne peut pas en tirer beaucoup d'information que la classe de complexité d'un algorithme
Il y a un problème dans la phrase là. Il manque un "plus" après "beaucoup", non ?
On ne peut pas en tirer beaucoup d'information que la classe de complexité d'un algorithme, et ainsi les conséquences sur la dynamique des performances en fonction de la taille du problème.
Le "ainsi" me paraît bizarre. Ca se comprend mais je ferais plutôt comme ça : "On ne peut pas en tirer beaucoup plus d'informations que la classe de complexité d'un algorithme et que les conséquences sur la dynamique des performances en fonction de la taille du problème.".
J'insiste sur le mot dynamique
Guillemets ?
J'insiste sur le mot dynamique comme pour dire
Le "comme" fait bizarre.
les lacunes de leur prédécesseur
"prédécesseure" ?
elles sont un pas en avant vers une meilleure caractérisation en amont
"elles constituent" ?
À contrario, les problèmes non convexes seront généralement très difficiles
A contrario
non-convexes
et les algorithmes non efficaces, voire dans le pire des cas, aucun algorithme efficace ne peut exister
Qu'entends-tu par "efficace" ?
Enfin, avec la multiplication des problèmes non-convexes, des techniques satisfaisantes en pratique ont vu le jour
J'imagine que tu parles des métaheuristiques ?
ont fait emerger de nouveaux besoins
émerger
déplacer l'étude de l'efficacité du couple problème-méthode, de la méthode vers le problème
La virgule me semble en trop.
pour le plus grand nombre de connaitre à minima
a minima
les avancés de ces travaux et la classification des problèmes
avancées
References
Références
Crédits illustrations
des illustrations ?
L'ensemble des images jusqu'à « Une question de domaine » ont été crées
a été créé
et placées dans le domaine public.
et est placé
et celles de la section « Convexe versus non-convexe »
versus
L'animation de la section » Convexe versus non-convexe »
versus
Aucune modification n'a été effectué sur l'oeuvre.
effectuée
Aucune modification n'a été effectué sur l'oeuvre.
effectuée