Hercule Poireau1 est invité aux vœux de nouvelle année par l’ambassadeur de Belgique au Royaume-Uni. Pour faire patienter ses invités avant et pendant le discours, l’ambassadeur fournit à chacun de ses invités un plateau de quinze (trois lignes de cinq) chocolats belges, une invention d’un grand créateur : des rochers en chocolat fourrés à la noisette.
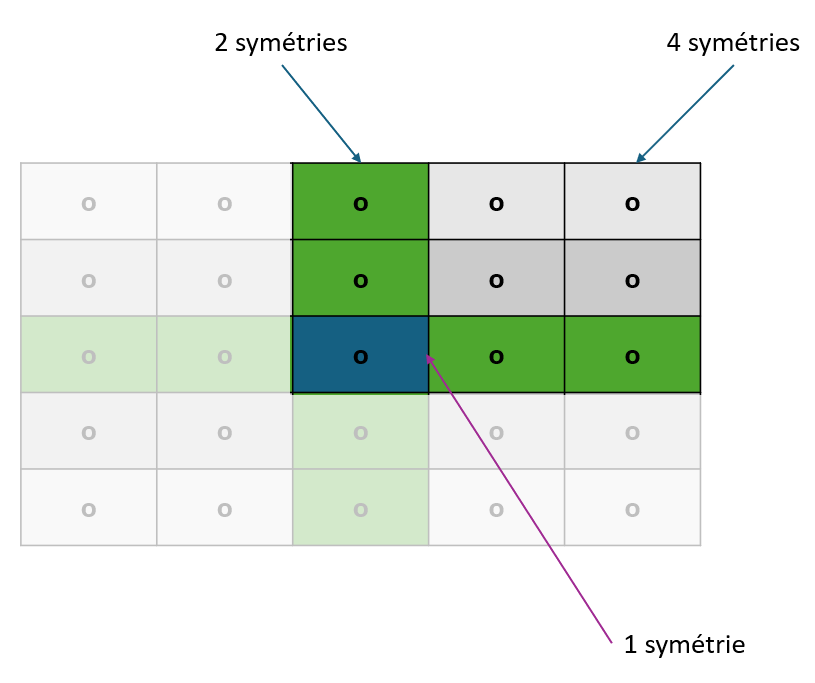
Hercule Poireau se régale d’avance à l’idée de savourer ces délices. Mais, alors qu’il admire les superbes chocolats, une question lui tricote le cervelet : lui qui est féru d’ordre et de méthode, arrivera-t-il à manger ses chocolats, un par un, de façon à ce que le motif (après éventuel arrangement) soit toujours symétrique selon les deux axes ? Devra-t-il rogner sur ses principes et ne se contenter d’une simple et peu satisfaisante symétrie centrale ?
Vérifiez si Hercule Poireau pourra satisfaire son envie de chocolat et son besoin pathologique de symétries. Si oui, aidez-le en lui proposant l’intégralité des rangements possibles pour chaque nombre de chocolat restant.
Une fois le discours de l’ambassadeur terminé, Hercule Poireau se pose une autre question : cette histoire de symétrie est-elle possible pour toutes les taille de plateaux de chocolats ?
L’exercice avec un plateau de 5 x 3 est assez léger pour être traité par force brute par n’importe quel ordinateur actuel en un temps négligeable.
Solution pour les symétries XY
Symétries XY pour 15 rochers (1 variante)
●●●●●
●●●●●
●●●●●
Symétries XY pour 14 rochers (1 variante)
●●●●●
●●○●●
●●●●●
Symétries XY pour 13 rochers (3 variantes)
●●○●● ●●●●● ●●●●●
●●●●● ○●●●○ ●○●○●
●●○●● ●●●●● ●●●●●
Symétries XY pour 12 rochers (3 variantes)
●●○●● ●●●●● ●●●●●
●●○●● ○●○●○ ●○○○●
●●○●● ●●●●● ●●●●●
Symétries XY pour 11 rochers (5 variantes)
○●●●○ ●○●○● ●●○●● ●●○●● ●●●●●
●●●●● ●●●●● ○●●●○ ●○●○● ○○●○○
○●●●○ ●○●○● ●●○●● ●●○●● ●●●●●
Symétries XY pour 10 rochers (5 variantes)
○●●●○ ●○●○● ●●○●● ●●○●● ●●●●●
●●○●● ●●○●● ○●○●○ ●○○○● ○○○○○
○●●●○ ●○●○● ●●○●● ●●○●● ●●●●●
Symétries XY pour 9 rochers (7 variantes)
○●○●○ ○●●●○ ○●●●○ ●○○○● ●○●○● ●○●○● ●●○●●
●●●●● ○●●●○ ●○●○● ●●●●● ○●●●○ ●○●○● ○○●○○
○●○●○ ○●●●○ ○●●●○ ●○○○● ●○●○● ●○●○● ●●○●●
Symétries XY pour 8 rochers (7 variantes)
○●○●○ ○●●●○ ○●●●○ ●○○○● ●○●○● ●○●○● ●●○●●
●●○●● ○●○●○ ●○○○● ●●○●● ○●○●○ ●○○○● ○○○○○
○●○●○ ○●●●○ ○●●●○ ●○○○● ●○●○● ●○●○● ●●○●●
Symétries XY pour 7 rochers (7 variantes)
○○●○○ ○●○●○ ○●○●○ ○●●●○ ●○○○● ●○○○● ●○●○●
●●●●● ○●●●○ ●○●○● ○○●○○ ○●●●○ ●○●○● ○○●○○
○○●○○ ○●○●○ ○●○●○ ○●●●○ ●○○○● ●○○○● ●○●○●
Symétries XY pour 6 rochers (7 variantes)
○○●○○ ○●○●○ ○●○●○ ○●●●○ ●○○○● ●○○○● ●○●○●
●●○●● ○●○●○ ●○○○● ○○○○○ ○●○●○ ●○○○● ○○○○○
○○●○○ ○●○●○ ○●○●○ ○●●●○ ●○○○● ●○○○● ●○●○●
Symétries XY pour 5 rochers (5 variantes)
○○○○○ ○○●○○ ○○●○○ ○●○●○ ●○○○●
●●●●● ○●●●○ ●○●○● ○○●○○ ○○●○○
○○○○○ ○○●○○ ○○●○○ ○●○●○ ●○○○●
Symétries XY pour 4 rochers (5 variantes)
○○○○○ ○○●○○ ○○●○○ ○●○●○ ●○○○●
●●○●● ○●○●○ ●○○○● ○○○○○ ○○○○○
○○○○○ ○○●○○ ○○●○○ ○●○●○ ●○○○●
Symétries XY pour 3 rochers (3 variantes)
○○○○○ ○○○○○ ○○●○○
○●●●○ ●○●○● ○○●○○
○○○○○ ○○○○○ ○○●○○
Symétries XY pour 2 rochers (3 variantes)
○○○○○ ○○○○○ ○○●○○
○●○●○ ●○○○● ○○○○○
○○○○○ ○○○○○ ○○●○○
Symétries XY pour 1 rochers (1 variante)
○○○○○
○○●○○
○○○○○
Symétries XY pour 0 rochers (1 variante)
○○○○○
○○○○○
○○○○○
Solution pour les symétries centrales
Symétries centrales pour 15 rochers (1 variante)
●●●●●
●●●●●
●●●●●
Symétries centrales pour 14 rochers (1 variante)
●●●●●
●●○●●
●●●●●
Symétries centrales pour 13 rochers (7 variantes)
○●●●● ●○●●● ●●○●● ●●●○● ●●●●○ ●●●●● ●●●●●
●●●●● ●●●●● ●●●●● ●●●●● ●●●●● ○●●●○ ●○●○●
●●●●○ ●●●○● ●●○●● ●○●●● ○●●●● ●●●●● ●●●●●
Symétries centrales pour 12 rochers (7 variantes)
○●●●● ●○●●● ●●○●● ●●●○● ●●●●○ ●●●●● ●●●●●
●●○●● ●●○●● ●●○●● ●●○●● ●●○●● ○●○●○ ●○○○●
●●●●○ ●●●○● ●●○●● ●○●●● ○●●●● ●●●●● ●●●●●
Symétries centrales pour 11 rochers (21 variantes)
○○●●● ○●○●● ○●●○● ○●●●○ ○●●●● ○●●●● ●○○●● ●○●○● ●○●●○ ●○●●● ●○●●● ●●○○● ●●○●○ ●●○●● ●●○●● ●●●○○ ●●●○● ●●●○● ●●●●○ ●●●●○ ●●●●●
●●●●● ●●●●● ●●●●● ●●●●● ○●●●○ ●○●○● ●●●●● ●●●●● ●●●●● ○●●●○ ●○●○● ●●●●● ●●●●● ○●●●○ ●○●○● ●●●●● ○●●●○ ●○●○● ○●●●○ ●○●○● ○○●○○
●●●○○ ●●○●○ ●○●●○ ○●●●○ ●●●●○ ●●●●○ ●●○○● ●○●○● ○●●○● ●●●○● ●●●○● ●○○●● ○●○●● ●●○●● ●●○●● ○○●●● ●○●●● ●○●●● ○●●●● ○●●●● ●●●●●
Symétries centrales pour 10 rochers (21 variantes)
○○●●● ○●○●● ○●●○● ○●●●○ ○●●●● ○●●●● ●○○●● ●○●○● ●○●●○ ●○●●● ●○●●● ●●○○● ●●○●○ ●●○●● ●●○●● ●●●○○ ●●●○● ●●●○● ●●●●○ ●●●●○ ●●●●●
●●○●● ●●○●● ●●○●● ●●○●● ○●○●○ ●○○○● ●●○●● ●●○●● ●●○●● ○●○●○ ●○○○● ●●○●● ●●○●● ○●○●○ ●○○○● ●●○●● ○●○●○ ●○○○● ○●○●○ ●○○○● ○○○○○
●●●○○ ●●○●○ ●○●●○ ○●●●○ ●●●●○ ●●●●○ ●●○○● ●○●○● ○●●○● ●●●○● ●●●○● ●○○●● ○●○●● ●●○●● ●●○●● ○○●●● ●○●●● ●○●●● ○●●●● ○●●●● ●●●●●
Symétries centrales pour 9 rochers (35 variantes)
○○○●● ○○●○● ○○●●○ ○○●●● ○○●●● ○●○○● ○●○●○ ○●○●● ○●○●● ○●●○○ ○●●○● ○●●○● ○●●●○ ○●●●○ ○●●●● ●○○○● ●○○●○ ●○○●● ●○○●● ●○●○○ ●○●○● ●○●○● ●○●●○ ●○●●○ ●○●●● ●●○○○ ●●○○● ●●○○● ●●○●○ ●●○●○ ●●○●● ●●●○○ ●●●○○ ●●●○● ●●●●○
●●●●● ●●●●● ●●●●● ○●●●○ ●○●○● ●●●●● ●●●●● ○●●●○ ●○●○● ●●●●● ○●●●○ ●○●○● ○●●●○ ●○●○● ○○●○○ ●●●●● ●●●●● ○●●●○ ●○●○● ●●●●● ○●●●○ ●○●○● ○●●●○ ●○●○● ○○●○○ ●●●●● ○●●●○ ●○●○● ○●●●○ ●○●○● ○○●○○ ○●●●○ ●○●○● ○○●○○ ○○●○○
●●○○○ ●○●○○ ○●●○○ ●●●○○ ●●●○○ ●○○●○ ○●○●○ ●●○●○ ●●○●○ ○○●●○ ●○●●○ ●○●●○ ○●●●○ ○●●●○ ●●●●○ ●○○○● ○●○○● ●●○○● ●●○○● ○○●○● ●○●○● ●○●○● ○●●○● ○●●○● ●●●○● ○○○●● ●○○●● ●○○●● ○●○●● ○●○●● ●●○●● ○○●●● ○○●●● ●○●●● ○●●●●
Symétries centrales pour 8 rochers (35 variantes)
○○○●● ○○●○● ○○●●○ ○○●●● ○○●●● ○●○○● ○●○●○ ○●○●● ○●○●● ○●●○○ ○●●○● ○●●○● ○●●●○ ○●●●○ ○●●●● ●○○○● ●○○●○ ●○○●● ●○○●● ●○●○○ ●○●○● ●○●○● ●○●●○ ●○●●○ ●○●●● ●●○○○ ●●○○● ●●○○● ●●○●○ ●●○●○ ●●○●● ●●●○○ ●●●○○ ●●●○● ●●●●○
●●○●● ●●○●● ●●○●● ○●○●○ ●○○○● ●●○●● ●●○●● ○●○●○ ●○○○● ●●○●● ○●○●○ ●○○○● ○●○●○ ●○○○● ○○○○○ ●●○●● ●●○●● ○●○●○ ●○○○● ●●○●● ○●○●○ ●○○○● ○●○●○ ●○○○● ○○○○○ ●●○●● ○●○●○ ●○○○● ○●○●○ ●○○○● ○○○○○ ○●○●○ ●○○○● ○○○○○ ○○○○○
●●○○○ ●○●○○ ○●●○○ ●●●○○ ●●●○○ ●○○●○ ○●○●○ ●●○●○ ●●○●○ ○○●●○ ●○●●○ ●○●●○ ○●●●○ ○●●●○ ●●●●○ ●○○○● ○●○○● ●●○○● ●●○○● ○○●○● ●○●○● ●○●○● ○●●○● ○●●○● ●●●○● ○○○●● ●○○●● ●○○●● ○●○●● ○●○●● ●●○●● ○○●●● ○○●●● ●○●●● ○●●●●
Symétries centrales pour 7 rochers (35 variantes)
○○○○● ○○○●○ ○○○●● ○○○●● ○○●○○ ○○●○● ○○●○● ○○●●○ ○○●●○ ○○●●● ○●○○○ ○●○○● ○●○○● ○●○●○ ○●○●○ ○●○●● ○●●○○ ○●●○○ ○●●○● ○●●●○ ●○○○○ ●○○○● ●○○○● ●○○●○ ●○○●○ ●○○●● ●○●○○ ●○●○○ ●○●○● ●○●●○ ●●○○○ ●●○○○ ●●○○● ●●○●○ ●●●○○
●●●●● ●●●●● ○●●●○ ●○●○● ●●●●● ○●●●○ ●○●○● ○●●●○ ●○●○● ○○●○○ ●●●●● ○●●●○ ●○●○● ○●●●○ ●○●○● ○○●○○ ○●●●○ ●○●○● ○○●○○ ○○●○○ ●●●●● ○●●●○ ●○●○● ○●●●○ ●○●○● ○○●○○ ○●●●○ ●○●○● ○○●○○ ○○●○○ ○●●●○ ●○●○● ○○●○○ ○○●○○ ○○●○○
●○○○○ ○●○○○ ●●○○○ ●●○○○ ○○●○○ ●○●○○ ●○●○○ ○●●○○ ○●●○○ ●●●○○ ○○○●○ ●○○●○ ●○○●○ ○●○●○ ○●○●○ ●●○●○ ○○●●○ ○○●●○ ●○●●○ ○●●●○ ○○○○● ●○○○● ●○○○● ○●○○● ○●○○● ●●○○● ○○●○● ○○●○● ●○●○● ○●●○● ○○○●● ○○○●● ●○○●● ○●○●● ○○●●●
Symétries centrales pour 6 rochers (35 variantes)
○○○○● ○○○●○ ○○○●● ○○○●● ○○●○○ ○○●○● ○○●○● ○○●●○ ○○●●○ ○○●●● ○●○○○ ○●○○● ○●○○● ○●○●○ ○●○●○ ○●○●● ○●●○○ ○●●○○ ○●●○● ○●●●○ ●○○○○ ●○○○● ●○○○● ●○○●○ ●○○●○ ●○○●● ●○●○○ ●○●○○ ●○●○● ●○●●○ ●●○○○ ●●○○○ ●●○○● ●●○●○ ●●●○○
●●○●● ●●○●● ○●○●○ ●○○○● ●●○●● ○●○●○ ●○○○● ○●○●○ ●○○○● ○○○○○ ●●○●● ○●○●○ ●○○○● ○●○●○ ●○○○● ○○○○○ ○●○●○ ●○○○● ○○○○○ ○○○○○ ●●○●● ○●○●○ ●○○○● ○●○●○ ●○○○● ○○○○○ ○●○●○ ●○○○● ○○○○○ ○○○○○ ○●○●○ ●○○○● ○○○○○ ○○○○○ ○○○○○
●○○○○ ○●○○○ ●●○○○ ●●○○○ ○○●○○ ●○●○○ ●○●○○ ○●●○○ ○●●○○ ●●●○○ ○○○●○ ●○○●○ ●○○●○ ○●○●○ ○●○●○ ●●○●○ ○○●●○ ○○●●○ ●○●●○ ○●●●○ ○○○○● ●○○○● ●○○○● ○●○○● ○●○○● ●●○○● ○○●○● ○○●○● ●○●○● ○●●○● ○○○●● ○○○●● ●○○●● ○●○●● ○○●●●
Symétries centrales pour 5 rochers (21 variantes)
○○○○○ ○○○○● ○○○○● ○○○●○ ○○○●○ ○○○●● ○○●○○ ○○●○○ ○○●○● ○○●●○ ○●○○○ ○●○○○ ○●○○● ○●○●○ ○●●○○ ●○○○○ ●○○○○ ●○○○● ●○○●○ ●○●○○ ●●○○○
●●●●● ○●●●○ ●○●○● ○●●●○ ●○●○● ○○●○○ ○●●●○ ●○●○● ○○●○○ ○○●○○ ○●●●○ ●○●○● ○○●○○ ○○●○○ ○○●○○ ○●●●○ ●○●○● ○○●○○ ○○●○○ ○○●○○ ○○●○○
○○○○○ ●○○○○ ●○○○○ ○●○○○ ○●○○○ ●●○○○ ○○●○○ ○○●○○ ●○●○○ ○●●○○ ○○○●○ ○○○●○ ●○○●○ ○●○●○ ○○●●○ ○○○○● ○○○○● ●○○○● ○●○○● ○○●○● ○○○●●
Symétries centrales pour 4 rochers (21 variantes)
○○○○○ ○○○○● ○○○○● ○○○●○ ○○○●○ ○○○●● ○○●○○ ○○●○○ ○○●○● ○○●●○ ○●○○○ ○●○○○ ○●○○● ○●○●○ ○●●○○ ●○○○○ ●○○○○ ●○○○● ●○○●○ ●○●○○ ●●○○○
●●○●● ○●○●○ ●○○○● ○●○●○ ●○○○● ○○○○○ ○●○●○ ●○○○● ○○○○○ ○○○○○ ○●○●○ ●○○○● ○○○○○ ○○○○○ ○○○○○ ○●○●○ ●○○○● ○○○○○ ○○○○○ ○○○○○ ○○○○○
○○○○○ ●○○○○ ●○○○○ ○●○○○ ○●○○○ ●●○○○ ○○●○○ ○○●○○ ●○●○○ ○●●○○ ○○○●○ ○○○●○ ●○○●○ ○●○●○ ○○●●○ ○○○○● ○○○○● ●○○○● ○●○○● ○○●○● ○○○●●
Symétries centrales pour 3 rochers (7 variantes)
○○○○○ ○○○○○ ○○○○● ○○○●○ ○○●○○ ○●○○○ ●○○○○
○●●●○ ●○●○● ○○●○○ ○○●○○ ○○●○○ ○○●○○ ○○●○○
○○○○○ ○○○○○ ●○○○○ ○●○○○ ○○●○○ ○○○●○ ○○○○●
Symétries centrales pour 2 rochers (7 variantes)
○○○○○ ○○○○○ ○○○○● ○○○●○ ○○●○○ ○●○○○ ●○○○○
○●○●○ ●○○○● ○○○○○ ○○○○○ ○○○○○ ○○○○○ ○○○○○
○○○○○ ○○○○○ ●○○○○ ○●○○○ ○○●○○ ○○○●○ ○○○○●
Symétries centrales pour 1 rochers (1 variante)
○○○○○
○○●○○
○○○○○
Symétries centrales pour 0 rochers (1 variante)
○○○○○
○○○○○
○○○○○
Variante beaucoup plus difficile pour les plus motivés d’entre vous :
Quelles sont les positions des chocolats Hercule Poireau doit manger, et quels sont les déplacements qu’il doit effectuer, dans le but de minimiser les déplacements pour obtenir des motifs symétriques ?
- Toute coïncidence avec un personnage d’Agatha Christie ne serait que purement fortuite.↩