Trouver tout les sous-graphes de taille k

TW: noob en théorie des graphes

Salut,

En tant que chimiste théoricien, j’ai l’occasion de mesurer des paramètres géométriques tels que les angles dans des molécules. Par exemple,

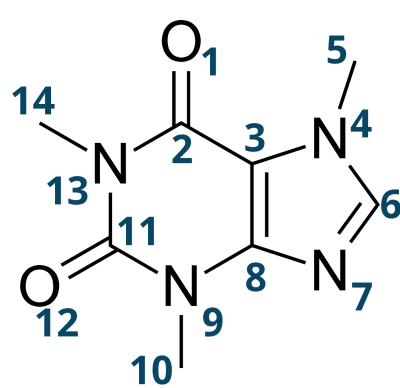
dans cette molécule, on voudrait par exemple connaitre l’angle entre les atomes 2, 3 et 4. La question qui se pose alors est "comment lister tout les angles possibles de cette molécule?".

Bien entendu, il s’agit d’un problème de théorie des graphes. Dit autrement, je cherche un algorithme qui me permet de lister tout les sous-graphes connecté de $k$-sommets ($k=3$ pour les angles, mais je suis également intéressé par $k=4$) dans un graphe non-dirigé (l’angle entre les atomes 2, 3 et 4 est évidement le même que celui entre les atomes 4, 3 et 2), mais qui peut contenir des cycles, comme le montre l’exemple ci-dessus.

Bien entendu, un "bête" algorithme bruteforce consisterai à lister tout les $k$-uplet de sommet, et à vérifier qu’ils sont effectivement connectés. Sauf que vu que le graphe est pas directionnel, il faut également que je supprime les doublons.

Est ce qu’il y aurai un alogorithme un peu plus malin ? Je me doute bien que ça va être un algoritme à la complexité algorithmique dégueulasse ($O(n^k)$ ?) mais peu m’importe, tant que je suis sur de les avoir tous, et une seule fois

Merci d’avance

EDIT: lorsqu’on fait des recherches sur Google, on est très vite orienté sur le problème des cliques. Or ce n’est pas ce que je veux, puisque je ne recherche pas des sous-graphes complets

Deja vu la densite du graphe, plutot que de tester tous les k-uplets de sommets, je ferais juste un parcours en profondeur de longueur $k$ depuis chaque sommet, histoire d’obtenir deja une liste de $k$-uplets candidats plus petite. Ensuite ca depend aussi de comment ton graphe est represente (comment tu recuperes les angles ?)

Salut,

Tu peux itérer sur les atomes de ta molécule, en les considérant comme le sommet d’un angle. Pour chaque atome/sommet, il te reste alors à prendre tous les paires d’atomes connectés et ça te donne tous les angles pour chaque sommet. Comme tu fais ça pour chaque sommet, tu as tous les angles.

Pour k=4, tu devrais pouvoir faire quelque chose de similaire en listant les liaison/transitions du graphe. Pour chaque liaison, tu regardes les paires d’atomes voisins de chaque extrémité (en prenant un d’un côté et un de l’autre).

Si tu veux d’autres k, j’ai pas mieux à proposer. Mais ça ressemble un peu dans l’esprit à ce qui était dit juste au-dessus. Tu peux peut-être construire tes solutions récursivement.

Ce n’est pas seulement une question de théorie des graphes, n’oublions pas qu’il s’agit de calculer des angle : c’est aussi une question de géométrie.
De ce point de vue, pour avoir un angle, il faut avoir une origine, point de concours de deux demi-droites.

Lees atomes qui ont un seul atome adjacent ne peuvent pas êtres à l’origine d’un angle !

Par ailleurs, c’est une question chimique. On sait bien que le carbone ou le silicium ont au plus 4 liaisons, tandis que le souffre peut en avoir 6. Il me semble que le nombre de liaisons d’un atome est très llimité. Donc, un algorithme efficient devrait considérer chaque atome en tant qu’origine éventuelle dun ou plusieurs angles. Le nombre d’angles est donc de l’ordre du nombre d’atomes.

Grillé par Aabu !

Salut,

De base, un algorithme sera forcément en $O({n \choose k})$ dans le pire cas : il suffit de voir que sur une clique, il faut bien générer tous les sous-graphes.

Ensuite, quelle est la taille de tes molécules ? Tant que tu restes sous mettons 100 atomes je ne suis pas sûr que le bruteforce soit la partie limitante de ton programme.

L’algorithme suivant me semble viable pour du bruteforce : https://cs.stackexchange.com/a/119943

Après vu tes graphes c’est probablement possible de faire mieux, vu l’absence de clique et le faible degré. N’empêche que ça serait marrant, une molécule en clique.

La piste de Lucas-84 ne fonctionne pas forcément (par exemple une DFS qui part de l’atome 2 ne verra pas le couple 1,2,3).

Mon idée serait d’avoir un parcours en largeur où tu parsd’une racine quelconque et tu gardes en mémoire, pour chaque noeud, ses voisins non encore visités dans une liste $L[noeud]$. Ensuite, en repartant de la racine tu rentres dans la fonction récursive suivante :

• Tu ajoutes le noeud courant au chemin en cours
• Pour chaque noeud fils (que tu trouves dans L[noeud]:
• Pour 0 <= i<= k:
• Tu génères les chemins de taille i qui partent du fils
• Tu génères les chemins de taille k-i qui n’utilisent pas le fils, mais partent d’un des voisins du fils (dans L[noeud])
• Tu effectues un produit cartésien sur ces deux ensembles de chemins partiels, tu te retrouves avec plein de chemins de longueur k
• Fin pour
• Tu gardes en mémoire ces chemins
• Fin pour

Merci à tous,

Ça confirme donc ce que je pensais suite à mes recherches: il n’existe pas spécialement d’algorithme dédié à ça. Par contre, je confirme qu’on part effectivement sur des structures moléculaires, donc des graphes au degrés très (très!) faible ($d\leq 4$ la plupart du temps, avec assez bien de $d=1$). Par contre, je vise des choses qui sont de l’ordre de $n=1000$. Je vais donc tester tout ça

La piste de Lucas-84 ne fonctionne pas forcément (par exemple une DFS qui part de l’atome 2 ne verra pas le couple 1,2,3).

J’ai pas compris le problème, le DFS donne un arbre de profondeur k à partir duquel on peut facilement obtenir les k-uplets candidats

Un parcours d’arbre classique ne suffit pas, tu peux avoir un k-uplet qui fait intervenir un noeud, et deux de ses fils dans l’arbre (pour $k=3$). De plus, ta DFS depuis le noeud $n$ va donner des chemins de longueur $k$ depuis $n$, mais tous les tuples ne sont pas forcément des chemins (par exemple pour $k=4$ dans le graphe donné tu vas avoir le couple 1, 2, 3, 13 qui ne correspond à aucun DFS, vu que ce n’est pas un chemin).

Edit : il y a peut-être aussi un souci au niveau des cycles du graphe.

Ok je pense que l’incomprehension vient juste de la question de quoi faire une fois qu’on a l’arbre du DFS. Comme tu le fais remarquer, effectivement on ne peut pas juste considerer les branches une par une. Tbh mon idee plus haut etait juste de considerer tous les k-uplets de sommets dans ces petits arbres, apres on peut faire plus malin si c’est toujours pas suffisant.

… Je sais.

Bon, bah en fait, la solution naïve est compétitive. En utilisant networkx (donc on utilise bien un dictionnaire), j’ai:

import networkx
import itertools
import timeit

from typing import Iterable


def find_subgraphs_naive(g: networkx.Graph, k: int) -> Iterable[tuple]:
    seen = set()
    for subgraph in itertools.permutations(g.nodes, k):
        is_path = True
        for u, v in zip(subgraph[:-1], subgraph[1:]):
            if not g.has_edge(u, v):
                is_path = False
                break

        if is_path and tuple(reversed(subgraph)) not in seen:
            seen.add(subgraph)
            yield subgraph


def find_subgraphs(g: networkx.Graph, k: int) -> Iterable[tuple]:

    def paths(root: int, n: int = k - 1, previous_path: tuple = ()):
        previous_path += (root,)
        if n == 0:
            yield previous_path
        else:
            for j in g.adj[root]:
                if j in previous_path:
                    continue
                yield from paths(j, n - 1, previous_path)

    for i in g.nodes:
        for subgraph in paths(i):
            if subgraph[-1] < i:  # avoid loop and reverse
                continue

            yield subgraph


def test_find_subgraphs():
    g = networkx.circular_ladder_graph(100_000)

    number = 1_000_000

    print('naive', timeit.timeit(lambda: find_subgraphs_naive(g, 4), number=number) / number * 1_000_000, 'µs')
    print('paths', timeit.timeit(lambda: find_subgraphs(g, 4), number=number) / number * 1_000_000, 'µs')


def test_subgraphs_equal():
    g = networkx.circular_ladder_graph(20)
    assert set(find_subgraphs_naive(g, 4)) == set(find_subgraphs(g, 4))

Et j’obtiens …

============================= test session starts ==============================
collecting ... collected 2 items

test_graphs.py::test_find_subgraphs PASSED                               [ 50%]naive 0.2748499509762041 µs
paths 0.33806083200033754 µs

test_graphs.py::test_subgraphs_equal PASSED                              [100%]

========================= 2 passed, 1 warning in 2.37s =========================

Donc sur ma machine, tester naïvement toute les possibilités n’est même pas si couteux, même sur des grands graphes (j’ai aussi testé sur des graphes complet, et ça passe). C’est même moins couteux que d’essayer de naviguer dans l’arbre (bon, en même temps, tripoter des tuple dans tout les sens est peut être pas très malin).

Par contre, je ne me rendais pas compte que comparer des set(), c’était si couteux

Donc merci

Oh, bien vu, je viens de me faire avoir comme un bleu

je me disais aussi que mes temps variait pas de beaucoup quand j’augmentais la taille du graphe