Bonsoir à tous,
Je travaille actuellement quelques méthodes numériques pour approximer les équations aux dérivées partielles (que j'abrège EDP). En particulier, je m'intéresse à l'équation de transport (d'inconnue la fonction
Pour approximer une solution
Enfin, pour pouvoir calculer effectivement les quantité 
Bon, ça c'était pour les définitions et les notations. Je sais que ça fait beaucoup, mais ainsi va la vie. o/ J'ai démontré que mon schéma numérique est d'ordre 1 en temps et en espace. Plus précisément,
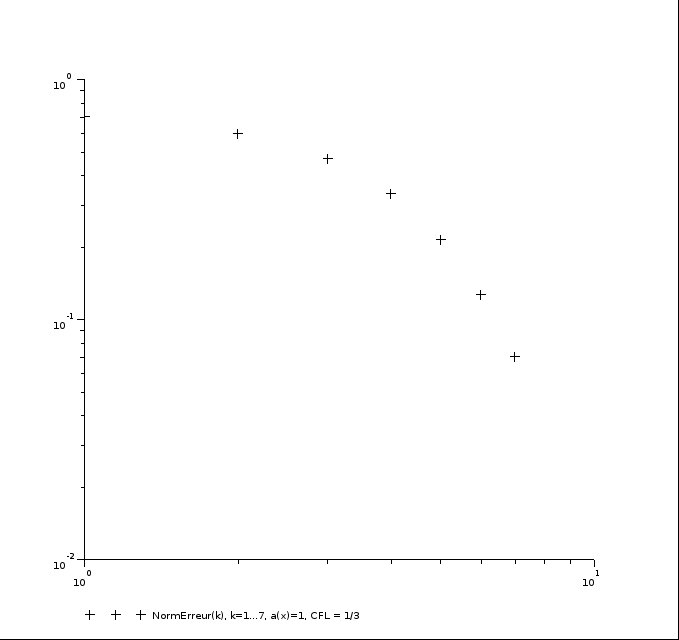
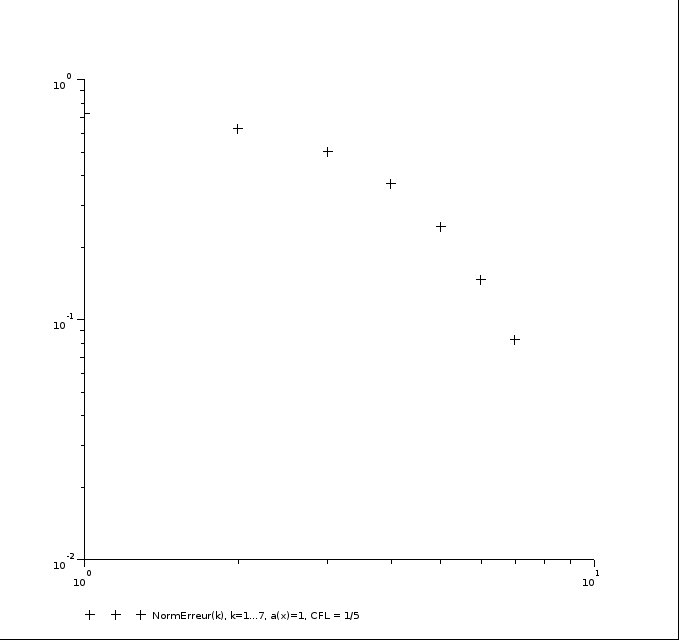
Mais ensuite, j'ai quelque-chose d'un peu surprenant. Pour faire quelques tests, j'ai pris des fonctions
Ce qui me surprend beaucoup c'est que le graphe obtenu n'est pas linéaire ; à vrai dire il n'est même pas affine. Et c'est là que j'ai un gros doute. En effet, il me semble que normalement, l'erreur de consistance en échelle log-log est supposée être linéaire en le pas du maillage. En tout cas, je sais que c'est vrai lorsqu'il y a seulement une dimension d'espace et pas de temps. Que dire lorsqu'il y a une dimension d'espace et de temps ? A-t-on également linéarité de l'erreur en échelle log-log ? Est-ce le fait que mes courbes ne soient pas linéaires implique que mon implémentation du schéma est fausse ? Si non, avez vous des références bibliographiques ou des liens à me proposer, voire des idées de preuves, pour expliquer pourquoi l'erreur n'est pas linéaire dans ce cas ?
Merci beaucoup d'avance à tous. Je sais que la question peut paraître imbuvable, à cause des notations. Mais il y a quand même des maths intéressantes cachées derrière, c'est promis. 




 Dans ma tête j'ai pensé à redéfinir l'exponentiation à partir du log en base 10 pour pouvoir sortir le
Dans ma tête j'ai pensé à redéfinir l'exponentiation à partir du log en base 10 pour pouvoir sortir le 