Condition de roulement sans glissement

Bonjour à tous !

Soit un cylindre creux de rayon extérieur $r$ et de rayon intérieur $r_0$.
Pour le schéma ci-dessous, écrivez la condition de roulement sans glissement du cylindre sur le profil circulaire de rayon $R$.

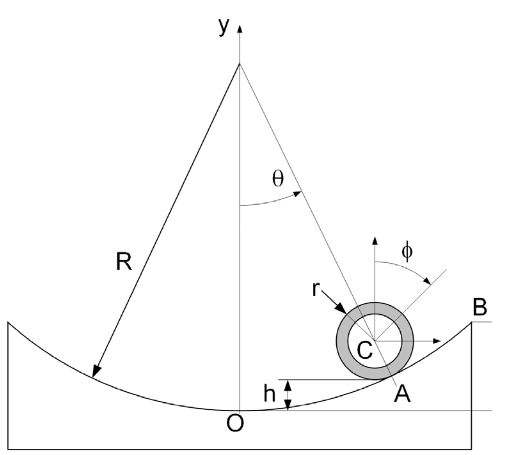
Je pense que c’est :  $\dot \phi r = R\dot \theta$ (remarquez les points pour la dérivée temporelle) mais mon corrigé propose plutôt : $\dot \phi r = (R - r)\dot \theta$.

Je pense que mon corrigé a une erreur, quelle est votre impression ?

Salut,

Ton corrigé est juste, regarde la distance parcourue par le centre de la roue… Un cas extrême est de prendre $r=R$, tu ne peux pas rouler sans glisser et donc $\dot\phi=0$.

Je ne comprends pas, j’ai un autre raisonnement :

Si le cylindre avance grâce à une rotation $\Delta \phi$, le cylindre parcours la distance $d = r \Delta \phi$.  Il existe un arc $\Delta \theta$ interceptant cette distance parcourue tel que :

$R \Delta \theta = d = r \Delta \phi$

Cette relation est vraie en particulier si l’on prend une rotation $d\phi$, ce qui donne :

$Rd\theta = rd \phi$

En divisant par $dt$ dans les deux membres de l’équation, on retrouve $R\dot \theta = r \dot \phi$.

Où est mon erreur ?

Précision : quand je parle de la distance parcourue par le cylindre, je parle bien de la distance parcourue au sol. Ce n’est donc pas la même distance que celle parcourue par le centre de masse du cylindre.

@adri1 tu as bien raison car mon équation n’est pas vérifiée pour $r \to R$ par contre je ne vois pas trop où j’ai fait une faute de raisonnement.

En l’occurence, pour rouler sans glisser, c’est la distance parcourue par le centre de figure (pas de masse, c’est sûr) qui doit être égale à celle parcourue par le bord.

Merci pour l’astuce, je vais retenir ça !