Bonjour,
J’étudie la trajectoire des missions Apollo (pour potentiellement en faire un article) et j’en profite pour apprendre le Rust.
Un peu de contexte : j’ai implémenté un algorithme itératif (je me perdais dans la version analytique) qui calcule la force d’attraction de la Terre et de la Lune pour en déduire l’accéleration de mon vaisseau. J’intègre deux fois pour en déduire la position.
En pratique ca donne ça (cliquez pour agrandir) : 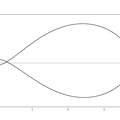 1.
1.
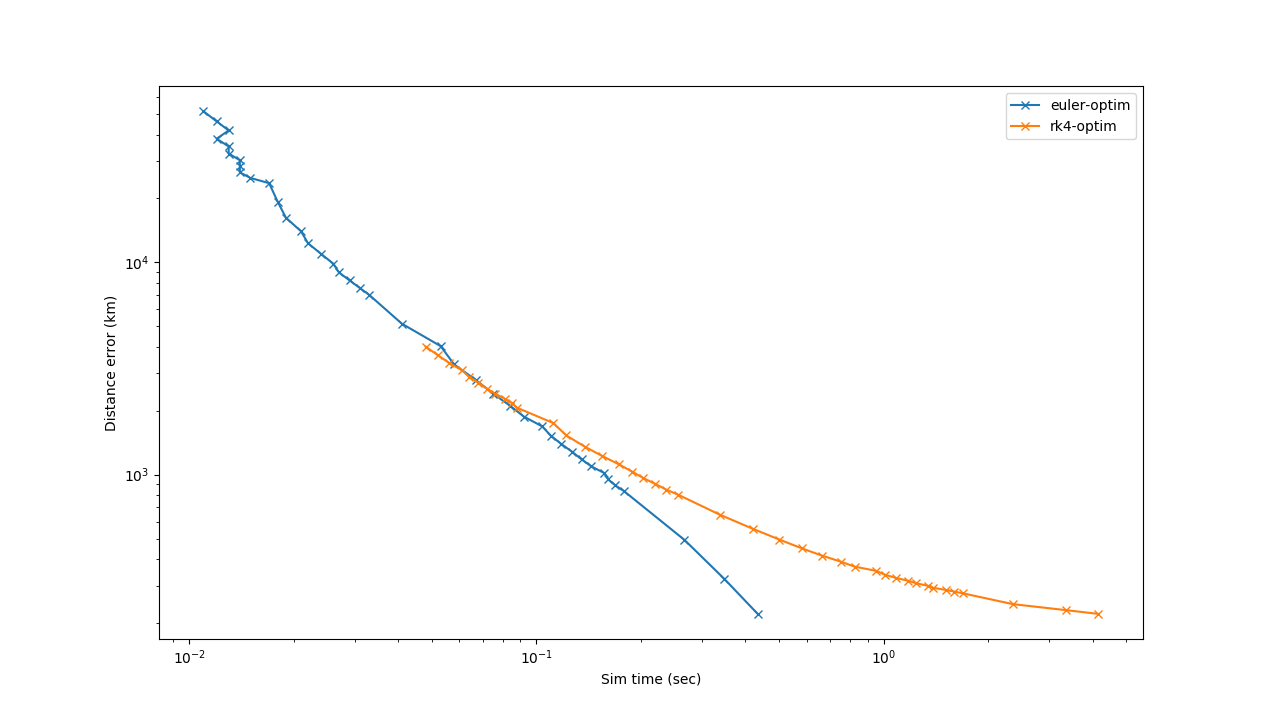
J’ai donc un algorithme qui fonctionne, mais il est (relativement) lent, et j’aimerais l’optimiser. Le but est non seulement d’avoir quelque chose le plus rapide possible, mais tant qu’on y est, faire un petit benchmark (et un autre article, la liste s’allonge vite !) : j’ai commencé par l’implémenter en Python, mais vu la lenteur je l’ai re-implémenté en Rust et en C.
Sans plus attendre, voici les version C et Rust (Python restera loin derrière dans tous les cas), ainsi qu’un petit Makefile pour compiler et exécuter tout ça. Normalement le code est simple à comprendre, mais je peux détailler si besoin.
Actuellement, j’obtiens 1050–1100 ms pour C et 1400–1500 ms pour Rust (et ne parlons pas de Python, on a un facteur 50 ou 100 !) (  Rust est plus lent ?!) (je parle de la partie "sim" uniquement, mais si vous voulez optimiser aussi la partie export, pourquoi pas
Rust est plus lent ?!) (je parle de la partie "sim" uniquement, mais si vous voulez optimiser aussi la partie export, pourquoi pas  ).
).
Ma requête est donc : quelles sont les pistes à explorer pour optimiser les version C et Rust (mais plutot Rust que je connais moins) ? Comme l’interet est d’apprendre Rust, si vous avez des remarques sur la forme, ou quoi que ce soit d’autre, je suis ouvert à tout 
Merci d’avance
-
Tout est à l’échelle ; distances en mètres ; repère orthonormé centré sur le barycentre Terre-Lune, en rotation avec le système, ce qui donne aux corps une position fixe. Pour info l’altitude initiale est de 185 km à comparer au 6378 km du rayon de la Terre et ~400 000 km de distance Terre-Lune.
↩




 ).
).