En 2014, un doctorant en physique nommé Jason Cole s’intéresse au placement de son routeur Wi-Fi dans son appartement et publie à ce sujet un article de blog où il y décrit la manière dont il s’y est pris pour étudier le problème, en se basant sur la résolution d’un problème de physique (l’article est intitulé helmhurts, pour des raisons qui vont vous sembler évidentes dans quelques instants). 8 ans plus tard, et dans le contexte d’un cours que je dois donner, j’ai décidé d’en coder ma propre implémentation.
Le but ? À partir d’un plan en deux dimensions représentant un appartement avec la position d’un routeur Wi-Fi (opérant à 2.4 GHz), déterminer les endroits de l’appartement qui seront couverts par celui-ci. Par exemple:
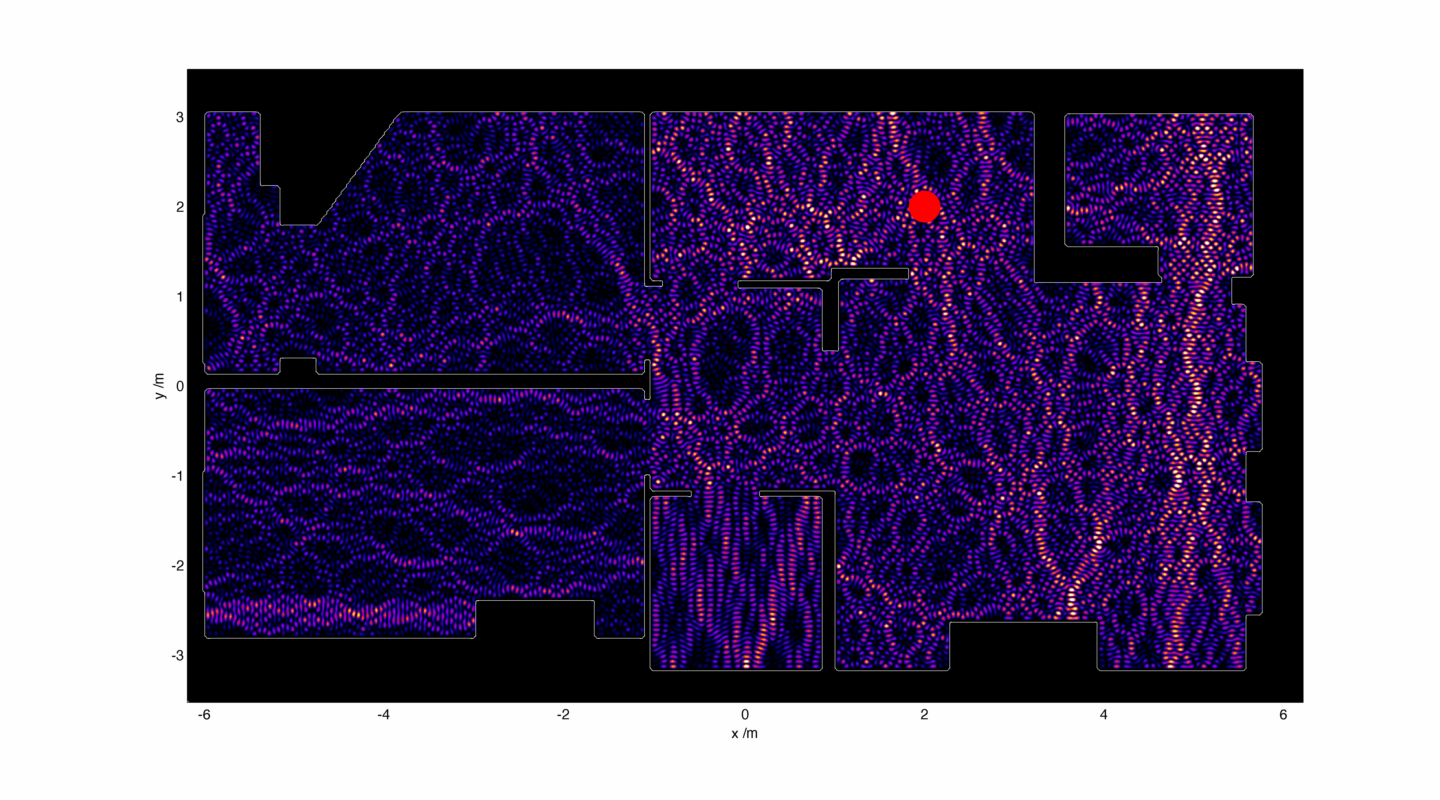
Par contre, mes images à moi seront vertes, pour donner un petit côté Matrix à la chose
Un peu de maths et de physique
Il est nécessaire de comprendre la notion de dérivée pour suivre cette partie.
À propos des ondes électromagnétiques
Une onde est la propagation d’une perturbation produisant sur son passage une variation réversible des propriétés physiques locales du milieu et dont la vitesse de propagation dépend des caractéristiques du milieu en question. Plus précisément, une onde électromagnétique est l’oscillation du champ électrique (et magnétique) générées par des particules chargées qui accélèrent (ou par un dipôle oscillant).
Quand on parle de rayonnement électromagnétique, les équations de Maxwell ne sont jamais bien loin. Sous les conditions adéquates, la propagation d’une onde est régie par l'équation inhomogène des ondes (ou équation d’Alembert dans sa version homogène):
où est la vitesse de l’onde (qui, dans le vide, correspond à la vitesse de la lumière) et est généralement appelée "fonction source", car elle décrit les effets de la source d’onde sur le milieu. C’est une équation différentielle, ce qui signifie que toute fonction qui vérifie cette équation décrit effectivement le comportement d’une onde.
Par exemple: une onde monochromatique, c’est à dire , où est la pulsation de l’onde, avec ( est la longueur d’onde). En effet, en supposant , si on substitue dans l’équation ci-dessus,1
ou encore, en définissant le nombre d’onde ,
Cette dernière version est appelée équation (inhomogène) d’Helmholtz. Elle décrit le comportement scalaire d’une onde monochromatique, c’est à dire son intensité en fonction de la position.
Pour ajouter à la difficulté, cette équation n’est valable que pour un milieu homogène, dans lequel la vitesse de l’onde est constante. Si on passe d’un milieu à un autre, la vitesse de l’onde change, selon le principe de la réfraction (qui modifie également l’angle) et plus particulièrement de la loi de Snell-Descartes. Puisqu’on cherche à simuler l’évolution d’une onde dans un milieu complexe (contenant à priori de l’air et des murs), on va donc modifier notre formule:
où est une fonction dont le sens est le même que celui de l'indice de réfraction: pour une portion de l’espace composée d’air, si on a autre chose.
Ceci dit, cela ne suffit pas: en effet, cette modification permet de tenir compte des propriétés de réfraction d’un mur (diffusion de l’onde dans le matériau et réflexion partielle de l’onde à l’interface avec celui-ci), mais ne modélise pas l'absorption d’une partie de l’onde par le mur (si ce n’était pas le cas, les ondes traverseraient le mur avec à peu près la même intensité en sortie qu’en entrée, et le monde serait à la fois plus simple et plus compliqué). Pour faire cela, une manière de faire est de donner une certaine conductivité électrique à notre matériau, et donc modifier notre équation comme suis:2
où dans l’air et dans un matériau absorbant, et .
Les quantités et , en plus de dépendre de la position, dépendent aussi de la longeur d’onde. Par exemple, quand on parle de l’indice de réfraction d’un matériau, on parle d’un indice de réfraction mesuré à une certaine longueur d’onde, typiquement aux alentours de 590 nm pour ceux qu'on utilise couramment (dû au fait qu’on utilise généralement la raie D du sodium pour les mesurer). Ici, on considère une onde Wi-Fi, donc .
C’est cette équation que nous allons tenter par la suite de résoudre. Encore une fois: toute fonction qui vérifie cette équation décrit le comportement de notre onde dans le milieu (complexe) que nous allons considérer. Néanmoins, cette fonction est difficile à obtenir analytiquement pour une raison assez évidente: elle dépend de . Dit autrement, l’intensité de l’onde à une position donnée dépend de la source qui la génère (oui, ça semble assez logique dit comme ça ).
À la recherche d’une solution
Puisque obtenir une solution analytique est hors de question (exceptés cas très particuliers tels que ), on va se tourner vers une solution numérique en utilisant la méthode des différences finies. Le principe est le suivant: on peut approximer une dérivée sur une dimension comme suis:
où est choisi en pratique suffisamment petit pour donner une bonne approximation de la dérivée.
Si on défini une grille de points en 2 dimensions composées de rectangles de taille et où est la valeur de au point sur la grille, on a
Dès lors, notre équation différentielle devient
et ce pour chaque point de notre grille. Autrement dit, on a un ensemble de équations à résoudre, dont les inconnues sont les . On peut représenter ce problème sous forme matricielle, après avoir condensé nos éléments et en deux vecteurs colonnes:
ou plus simplement . Déterminer revient donc à inverser , puisque .
Problème de limites et limites du problème
On ne simule par un problème infini, loin s’en faut. Il faut donc gérer ce qui se passe aux limites de la simulation, en imposant des conditions au limite. Par exemple, pour déterminer , on a besoin de et , qui n’existent pas.
Plusieurs solutions s’offrent à nous, mais certaines sont plus intéressantes dans ce cas que d’autre. Soit notre domaine de simulation, dont les limites sont notées .
-
Conditions aux limites de Dirichlet: définir aux limites du domaine une valeur pour la fonction. Typiquement, on va définir . Bien que ce choix semble anodin (voir arbitraire), il a une conséquence intéressante: notre onde ne peut pas sortir du domaine de simulation (puisque sa valeur est de zéro en dehors de ).
-
Conditions aux limite de Neumann: à l’inverse, c’est cette fois la valeur de la dérivée de en qui sont fixées. En pratique, il suffit alors de rajouter un certain nombres d’équations le long de dans notre système. Ceci dit, il n’est possible d’obtenir une solution que si , ce qui n’est pas notre cas.
-
Conditions aux limites de Sommerfled: l’énergie rayonnée des sources doit se disperser à l’infini, et aucune energie ne peut rayonner de l’infini. Dans notre cas, cela revient à satisfaire
dans toutes les directions à partir de la source.
Bien entendu, c’est la troisième condition qui est la plus adaptée à notre cas. Néanmoins, elle est un peu compliquée à mettre en place, et je vais donc tricher, en entourant le domaine de simulation d’une couche absorbante3 d’une certain épaisseur, et dont les caractéristiques seront , combiné avec une condition de Dirichlet aux limites de celle-ci: .
Au dela de nos problèmes pratico-pratiques, mathématiquement parlant, imposer une condition aux limites est la seule manière d’obtenir une solution unique à notre équation différentielle, qui sinon est obtenue à une constante près.
- En fait, on fait la transformée de Fourier du problème↩
- En fait, ça reviendrait au même si on repartait des équations de Maxwell, mais dans un milieu conducteur↩
- formellement, cette idée s’inspire de la méthode dite des couches absorbantes parfaitement adaptées↩
Un peu de code
Le code est disponible sur Github.
En entrée
Maintenant qu’on sait ce qu’on veut simuler et comment on veut le simuler, voyons comment je m’y suis pris. Je souhaitais pouvoir partir d’une image telle que celle-ci:

Construction de la fonction source, contraste et conductivité
À partir de cette image, j’extrais une matrice qui contient les valeurs RGB des pixels de l’image, et je construis , et (chaque pixel correspond à une valeur , par simplicité). En l’occurrence, j’ai simplement choisi:
Les valeurs choisies sont purement arbitraires. En pratique, la valeur de 2.4 n’est pas trop éloignée de la valeur de l’indice de réfraction d’un mur (en béton), d’après mes prédécesseurs.1 La valeur de 0.1 pour la conductivité est probablement exagérée au regard des valeurs typiques pour d’autres matériaux (bien que cela dépende de la longeur d’onde employée). Finalement, la valeur de 1 pour la source est purement arbitraire, puisque ce qui m’intéresse ici c’est le contraste.
Je rajoute également une couche d’absorption autour du domaine. Pour sa taille, on conseille de la choisir équivalente à la longueur d’onde (le nombre de cases auquel cela va correspondre dépend de la résolution du plan). Une onde oscillant à 2.4 GHz correspond à une longueur d’onde d’environ 12 cm. À noter que dès lors, .
À propos de la résolution
Le choix de la résolution est plus important qu’il n’y parrait: on ne peut pas choisir n’importe quoi et espérer s’en sortir. En effet, la solution de l’équation d’Helmholtz dans le cas le plus simple [, , et avec une condition limite de type Dirichlet] est .
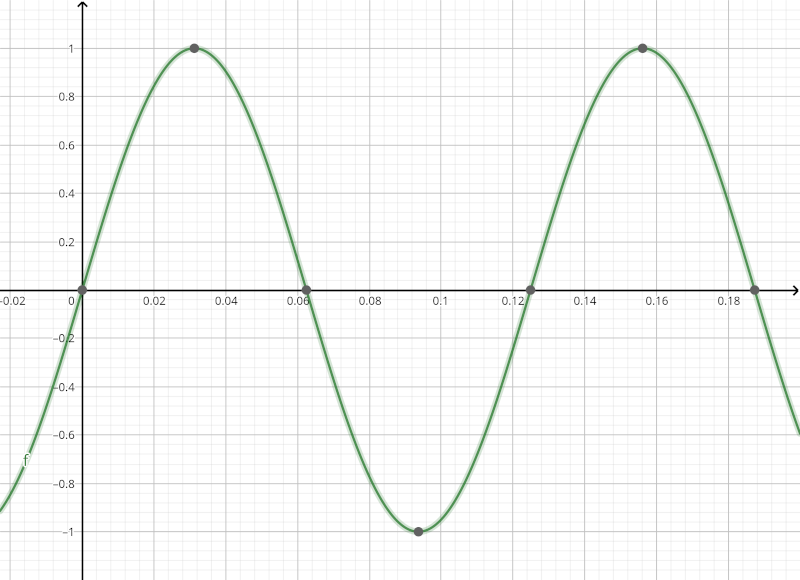
La distance entre deux maximums est d’à peu près 12 cm, c’est à dire la longueur d’onde. Si on veut obtenir ce résultat de manière correcte, il faut choisir une résolution suffisante (pour ceux qui savent ce que c’est, ça doit vous rappeler un problème d’échantillonnage). Typiquement,
où est le nombre de point qu’on souhaite utiliser pour décrire notre signal entre deux maximum.
Généralement, on veut , donc notre résolution pour 24 GHz devrait être de 1 pixel → 1cm. Pour traiter des problèmes intéressants (appartements de 50 à 100m²), il faudra donc utiliser des images dont les dimensions sont de plusieurs centaines de pixels pour chaque côté.
Résolution du système d’équation
Une conséquence du point précédent, c’est que le nombre d’inconnue est très important: autant que le nombre de pixels que contient l’image, plus celles pour la couche absorbante de taille , plus celles pour les conditions de Dirichlet, pour un total de . Si ça semble déjà beaucoup, rappelez vous que la matrice que nous devrons construire contient éléments (puisque chaque ligne correspond à l’équation pour un élément ).
Si on prend par exemple et , on a N=15 874 inconnues. est donc de taille 15 874 x 15 874, soit pas moins de 251 983 876 nombres complexes. Si chaque nombre complexe est stocké sur 128 bits (2 flottants en double précision, double), cette matrice requiert 3.75 Gio de mémoire. Et là, on a juste simulé un carré de 1 mètre de côté, soit rien de bien fou.
Heureusement pour nous, cette matrice est essentiellement vide. En effet, chaque ligne ne contient que 5 valeurs non-nulles, correspondant à , , , et . Sur notre exemple précédent, à peu près = 99.97% de la matrice est nulle, et ce nombre augmente avec . Pour gagner de la place, on peut imaginer partir du principe que les éléments de la matrice sont tous nuls, et ne stocker que les éléments qui ne le sont pas: c’est ce qu’on appelle une matrice creuse.
Toute bibliothèque un peu sérieuse permettant le calcul matriciel propose une structure de matrice creuse (sparse matrix) et les opérations qui lui sont associées. Dans mon cas, puisque j’utilise Python pour des raisons de facilité, c’est scipy.sparse que j’emploierai. À noter que dans la plupart des langages, une matrice creuse est immutable. Autrement dit, lui ajouter un élément après création est impossible, pour des raisons d’optimisation: il faut en recréer une nouvelle.
Pour créer matrice creuse, par exemple
la documentation recommande la manière suivante (qui est courante dans différentes librairies):
from scipy.sparse import csc_matrix # CSC = Compressed Sparse Column
indices_ligne = [0, 1, 2]
indices_colonne = [0, 1, 2]
valeurs = [1, 2, 3]
# autrement dit, A[0,0] = 1, A[1,1] = 2 et A[2,2] = 3
A = csc_matrix((valeurs, (indices_ligne, indices_colonne)), shape=(3, 3))
En effet, la fonction crée la matrice en utilisant la relation A[indice_ligne[k], indices_colonne[k]] = valeurs[k]. Autrement dit, il faut d’abord en lister les différentes valeurs.
Pour rappel, ce qui nous intéresse, c’est de résoudre le système .
Ceci dit, si on inverse directement pour calculer ensuite , on risque d’avoir une petite surprise: en effet, autant est effectivement creuse, autant il y a peu de chance que le soit, augmentant drastiquement le besoin en stockage ! C’est d’autant plus dommage que n’est qu’un intermédiaire. Heureusement, le module d'algèbre linéaire de scipy propose directement la fonction spsolve pour résoudre de tels systèmes, sans explicitement stocker :
import numpy
from scipy.sparse.linalg import spsolve
s = numpy.array([2, 3, 0])
E = spsolve(A, s) # E = [2, 1.5, 0]
Et vous pouvez vérifier que
Bref, il "suffit" de décrire chacun des éléments de tels que décrit plus haut et le tour est joué. Yapluka
En sortie
Une fois calculé, il n’y a plus qu’à l’afficher. Plutôt que de représenter directement , je vais m’intéresser à la puissance (en décibels), , où est le module de (qui est un nombre complexe). Une petite échelle de couleur plus tard (et l’utilisation d’un gradient pour détecter le contour des murs), voici le résultat:

On voit que la distribution est loin d’être uniforme. Vu la résolution choisie, c’est loin d’être inattendu (voir plus haut). En particulier, on remarque que les tâches (qui sont les endroits ou l’intensité est importante) sont d’à peu près 6px de hauteur, soit 6 cm dans la réalité, ce qui est raccord avec la longueur d’onde.
Afin de démontrer une dernière fois l’intérêt d’utiliser des matrices creuses, j’utilise l’exemple suivant:2


Le plan est à gauche, le résultat attendu à droite.
Sur mon Ryzen 5 1500X de 2018 et 8 processeurs (les codes de numpy.linalg et scipy.sparse.linalg étant parallélisé),
- le code python exploitant
scipy.sparse.linalget une matrice creuse s’exécute en 800 ms et consomme 82 Mio de mémoire - le code python utilisant
numpy.linalget donc la matrice complète s’exécute en 2 minutes 32 secondes et consomme 3.98 Gio de mémoire.
Il n’y a pas photo
- Globalement, trouver des valeurs d’indice de réfraction dans le domaine des Gigahertz, c’est chiant. Je m’y prends probablement mal, mais je ne trouve généralement pas grand chose.↩
- Sur l’image 200x300 ci-dessus, le code s’arrête bien vite avec l’erreur suivante :
numpy.core._exceptions._ArrayMemoryError: Unable to allocate 80.9 GiB for an array with shape (73676, 73676) and data type complex128. Ça se passe de commentaires↩
Jouons un peu !
Maintenant que j’ai un code fonctionnel ou toutes les constantes citées plus haut (indice de réfraction, conductivité, etc) sont devenu des variables, on va pouvoir s’amuser un peu. Et pour ce faire, je vous présente le plan de mon (ancien !) appartement. 50 m² (soit plus petit que celui de Jason Cole !) rien que pour moi et mon chat:

Disons que le plus intéressant, c’est de capter le Wi-Fi dans la chambre (pour les séries au calme), dans la cuisine (pour les recettes de cuisine et YouTube quand on cuisine) et dans les toilettes (parce que réseaux sociaux). Eh bien le résultat est le suivant:
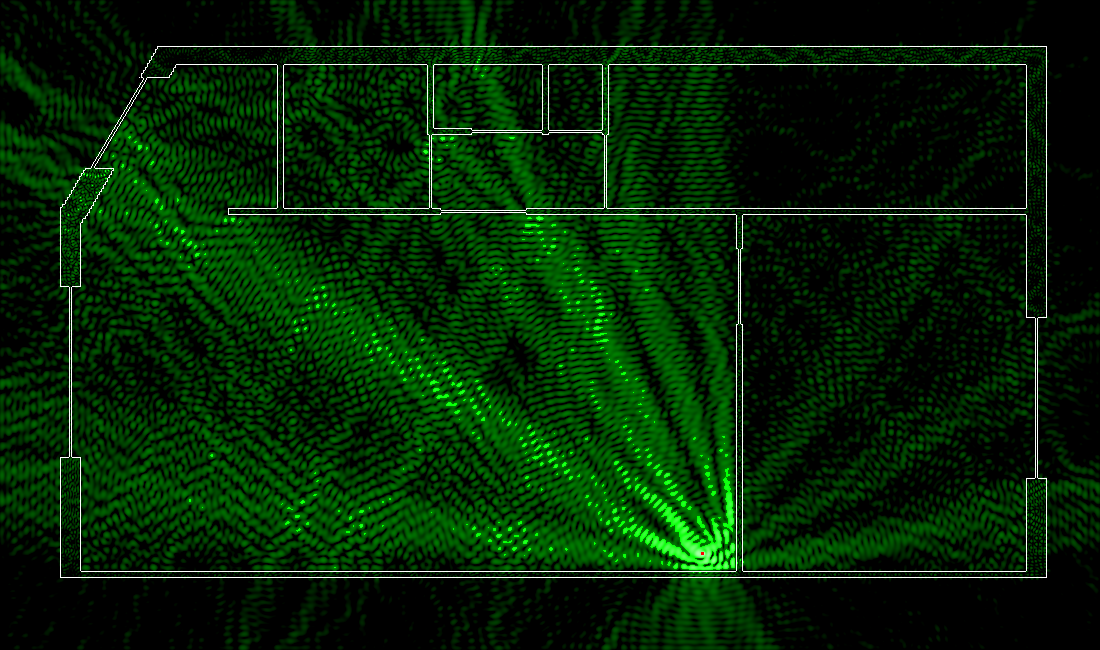
Clairement, la réflexion sur le mur aide à obtenir un bon signal au niveau de la cuisine et de la toilette. Par contre, et on l’avait déjà vu plus haut, les murs sont assez mauvais pour laisser passer du signal, ce qui fait que celui-ci est bien moins important dans la chambre. Notez bien que noir ne veut pas dire absence de signal, c’est juste une question d’échelle (ici entre -100 et -70 dB).
Changer de position
Évidement, je suis libre de déplacer mon routeur (à condition qu’il y ait une prise adaptée pas loin, ou que j’utilise un RJ45 assez long). Voici quelques résultats:

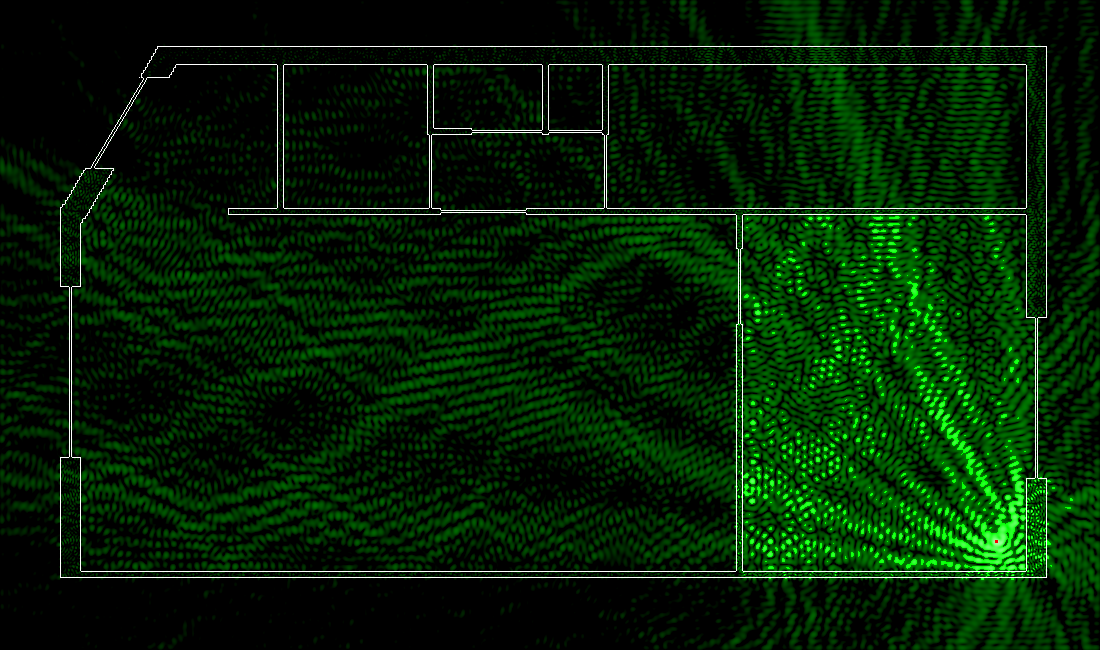

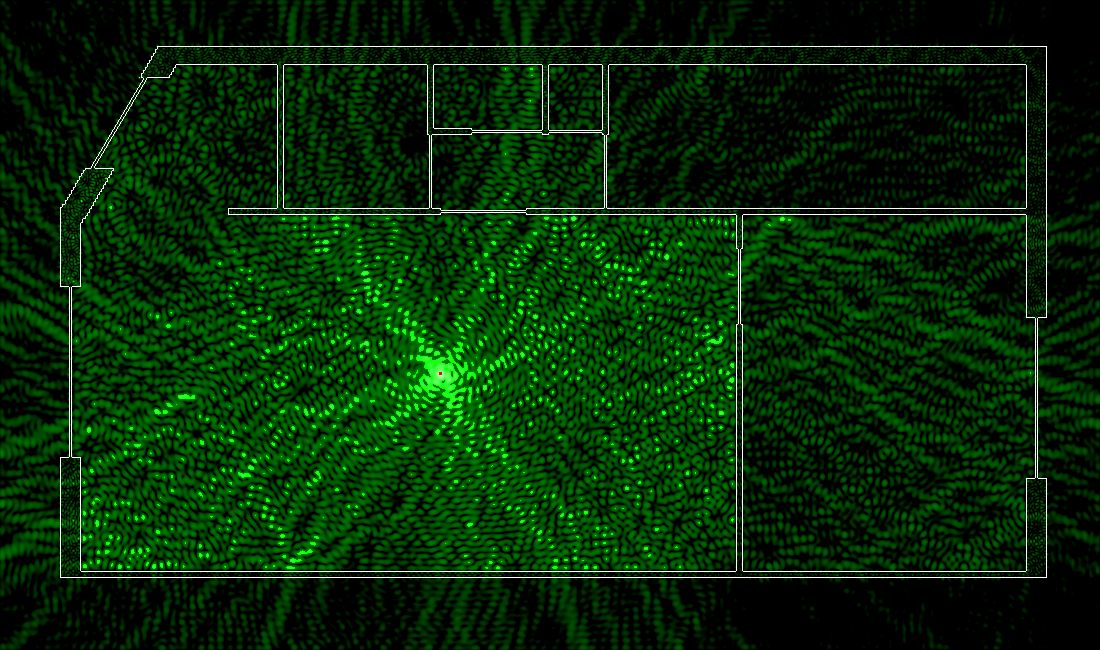
Ce qu’il faut retenir, c’est que les murs de ma simulation réfléchissent assez bien les ondes Wi-Fi. Je vais vous montrer quel est l’effet de changer l’indice de réfraction juste ci-dessous, mais notez bien que ce n’est pas tout à fait irréaliste: l’indice de réfraction d’un mur est élevé !
Changer l’indice de réfraction des murs
Pour le fun de la chose, imaginons que nos murs ont un indice de réfraction différent de 2.4. Essayons avec 2 extrêmes :

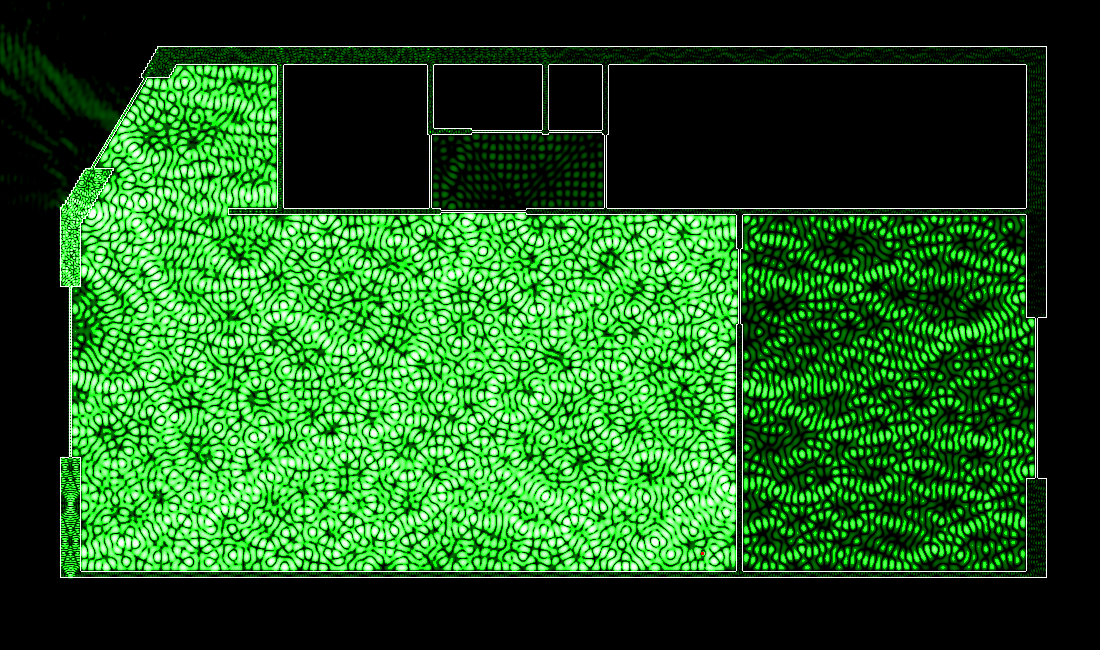
Ces différences s’expliquent par la loi de Fresnel:

La loi de Fresnel énonce que le coefficient de réflexion (c’est à dire le pourcentage de l’onde qui sera réfléchie) évolue comme
Pour , le coefficient de réflexion sera très proche de zéro, et une majorité de l’onde sera transmise dans le matériau. À l’inverse, pour , le coefficient de transmission sera beaucoup plus important. À noter qu’il existe un angle pour lequel la réflexion est totale, donné par , dont on voit bien qu’il diminue si augmente !
Changer la fréquence
Vous n’êtes pas sans savoir que depuis l’article de Jason Cole en 2014, il y a un peu d’eau qui a coulé sous les ponts et que le Wi-Fi à 5 GHz est maintenant courant (bien que la première implémentation de cette idée correspond à la norme IEEE 802.11a de … 1999). Vu que sa fréquence est plus élevée, la vitesse de transmission des données est supérieure avec cette fréquence. Par contre …

… Il passe beaucoup moins bien les murs. Bien que je ne parierais pas ma vie sur la qualité de cette simulation, c’est la réalité: un Wi-Fi 5 GHz est beaucoup plus sensible aux obstacles qu’un Wi-Fi 2.4 GHz, et s’atténuera plus vite.3
- Qui déjà plus proche de celui de l’eau ou du bois, si vous voulez un équivalent.↩
- Ce qui est, euuuh … Beaucoup, surtout à cette fréquence : l’indice de réfraction a tendance à tendre vers 1 lorsqu’on augmente la longueur d’onde / diminue la fréquence.↩
- D’autant qu’en pratique, l’indice de réfraction est légèrement supérieur pour une onde à 5 GHz qu’à 2.4 Ghz↩
Voilà, j’espère que cette petite modélisation vous à intéressé. Si vous deviez retenir quelque chose de tout ça, c’est que oui, vos murs réfléchissent les ondes Wi-Fi.
Bien entendu, la simulation est loin d’être parfaite, et on peut pointer les approximations suivantes:
- Il s’agit d’une modélisation en 2 dimensions, alors que vous et moi vivons dans un monde en 3 dimensions. Si ça semble un détail, n’oubliez pas que l’onde peut également se réfléchir sur le plafond et le sol. Par ailleurs, les pièces sont vides: certains objets (en particulier les objets métalliques !) peuvent drastiquement affecter le profil obtenu.
- La source est assez mal modélisée: normalement, on utilise une fonction delta de Dirac ou quelque chose qui s’en rapproche pour éviter d’être dépendant à la forme de la source. Néanmoins, dans la vraie vie , c’est une antenne dipôle qui équipe la plupart des routeurs, et qui devrait être décrite différemment (mais on est trop loin de mon domaine de compétence !).
- Le choix d’une fréquence fixe et unique de 2.4 GHz est également une approximation, puisque la bande Wi-Fi est découpé en canaux d’une largeur de 22 MHz compris entre 2.4 et 2.5 GHz. C’est un commentaire qui a déjà été fait à Jason Cole, pour ceux que ça intéresse.
- Le choix d’une modélisation indépendante du temps (équation de Helmholtz) est une approximation en soit (normalement, elle correspond à une situation d’équilibre). On peut employer une autre méthode basée sur les différences finies, la méthode finite difference time domain (FDTD) qui permet de tenir compte du temps, et inclus également l’effet du champ magnétique. Il n’est pas impossible que je tente cette méthode dans une suite
Sources et documents intéressants:
Je vous rappelle à toutes fins utiles que vous pouvez exécuter le code sur votre ordinateur, puisque celui-ci est disponible sur Github (vous avez même les images sources).
- L'article original de Jason Cole. À noter que dans son article, il écrit que la formule d’Helmholtz qu’il utilise est alors que doit être au numérateur, ce qu’il a expliqué en commentaire, mais on retrouve du coup cette erreur à d’autres endroits.
- Deux implémentations en Julia de l’idée originale de Jason Cole: ici et là, la seconde étant inspirée de la première. Bien que le Julia employé y soit un peu vieux (version 1.0) et que y soit au dénominateur, ça a été la base de mon code.
- Cet énoncé de projet par Bertrand Thierry, qui a le bon goût d’être en français, et dont vous reconnaîtrez qu’il m’a servi d’inspiration pour les deux premières parties.
- Cet article scientifique, qui décrit la méthode de l’équation d’Helmholtz (bien que ça ne soit pas le cœur du papier) et ou les constantes sont au bon endroit. L’idée d’utiliser la conductivité dans ma simulation est d’eux.
- Wikipédia, encore Wikipédia et toujours Wikipédia, comme en témoigne les très nombreux liens qui parsèment le document, bien que comme d’habitude en physique, la version anglaise est généralement plus fournie.


