IEEE 754 : Quand votre code prend la float

La première étape pour s’attaquer à IEEE 754 est de consulter sa page Wikipédia qui est plutôt bien fournie. Pour faire simple, il s’agit d’une norme permettant de définir les nombres flottants (à virgule si vous préférez) pour nos amis à puce de silicium. Elle définit entre autres une représentation des nombres flottants (dans cet article on va regarder le format dit binary32, qui correspond au type float en C, mais d’autres existent). La norme définit aussi des règles d’arrondis (et c’est un des aspects qui la rend robuste), un certain nombre d’opérations de base, de gestion des exceptions (les fameux NaN, Not a Number et autres infinis), ainsi que quelques recommandations. Dans cette série d’articles on va surtout s’intéresser à la représentation des nombres. La norme définit un agencement pour les flottants 32 bits.

Vous remarquez 3 parties dans ce schéma : le bit de signe, l’exposant et la mantisse. Concrètement, ma présentation préférée des flottants consiste à dire qu’il s’agit d’une approximation linéaire par morceaux de la valeur absolue du logarithme du nombre représenté. Ok, on peut faire plus clair (mais gardez ça en tête, c’est vraiment ce sur quoi on va s’appuyer dans cette série d’articles).

Pour préciser ça, on peut introduire des notations. On note $b_1b_2...b_{23}$ les 23 bits de la mantisse. Si on veut lier le nombre $x$ et sa représentation flottante, on peut écrire :

$x=(-1)^\text{signe}\times(1,b_1b_2...b_{\text{23}})_2\times2^{\text{exposant}-127}$

Où $y=(z)_k$ signifie "$y$ a pour représentation $z$ en base $k$".

Les nombres flottants sont normalisés (pour la plupart, on va y revenir). C’est nécessaire pour définir de manière unique l’exposant associé à un nombre. Ça permet aussi de gagner un bit de stockage, puisque le premier bit est forcément un 1, ce qui est montré dans l’équation précédente.

Vous noterez que l’exposant, sur 8 bits, est biaisé. Les valeurs autorisées pour les nombres normaux vont de $(00000001)_2$ à $(11111110)_2$, ce qui permet de représenter les nombres allant de $2^{−126} \approx 1.17 \times 10^{−38}$ à $(2 − 2^{−23}) × 2^{127} \approx 3.4 × 10^{38}$. C’est la même chose pour les négatifs, il suffit de changer le bit de signe. D’ailleurs on va arrêter rapidement de parler de nombres négatifs et simplement se concentrer sur les positifs, en gardant en tête que les nombres négatifs existent.

Dans la suite on appelle $n(x)$ la représentation flottante d’un nombre $x$. La partie exposant de la représentation binaire vaut $\lfloor log_2(x) \rfloor + 127$, avec pour digits $e_1e_2...e_8$. De plus, la mantisse est un nombre à 23 digits, croissant à peu près linéairement avec $x$ entre deux puissances de deux (derrière le « à peu près », il y a les règles d’arrondis de la norme). Dans ces conditions, on voit que :

Cette égalité est exacte pour les puissances de deux (la partie explicitement stockée de la mantisse est alors nulle). Si on trace sur un même graphe la représentation binaire d’un nombre x et l’expression approximative, on obtient la figure suivante :

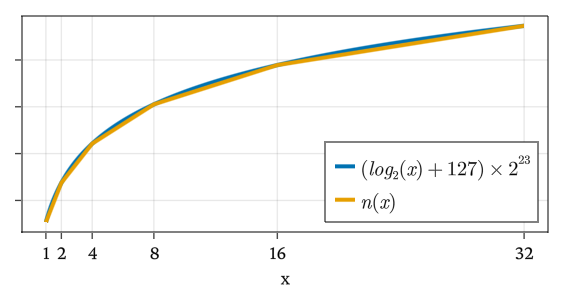
Cette proximité entre représentation binaire des flottants et logarithme va nous permettre dans les articles suivants de la série d’utiliser les propriétés du logarithme pour accélérer certains calculs. Mais pour la suite de cet article, je vous propose de continuer à lister quelques propriétés de la représentation flottante des nombres.

(de la représentation flottante)

Commençons par parler des très petits nombres. À ce stade j’espère que j’ai réussi à vous convaincre que la représentation d’un nombre flottant correspond à son logarithme. En fins mathématiciens que vous êtes, vous sentez probablement que cela va poser un problème autour de zéro. Évidemment cela a été pensé dans la norme.

Comme vous l’avez remarqué, le plus petit exposant autorisé est −126. Le plus petit nombre représentable est donc $(1,00000000000000000000000)_2 \times 2^{−126} \approx 1.17 \times 10^{−38}$. Enfin, le plus petit nombre normalisé ! En effet, la valeur d’exposant −127, qui correspond à un champ d’exposant nul a une signification bien précise : dans ce cas la mantisse se lit $(0,b_1...b_{23})_2$. On dit alors que le nombre est sous-normal. Cela signifie que le plus petit flottant positif représentable devient $(0,00000000000000000000001)_2×2^{−127} \approx 1.4\times10^{−45}$. En soustrayant 1 à la représentation binaire de ce dernier flottant, on obtient la représentation du zéro positif. Positif puisqu’on a pas oublié l’existence des nombres négatifs, donc en inversant le bit de signe on peut aussi obtenir le zéro négatif.

On a vu comment représenter les plus petit nombres, quoi de plus normal que de s’intéresser aux plus grands? Le plus grand nombre réel représentable sur un flottant dans notre norme est $(1,11111111111111111111111)_2 \times 2^{127} \approx 3.4 × 10^{38}$.

Si vous avez bien compté les valeurs autorisées pour l’exposant d’un nombre flottant, vous avez vu qu’il reste une valeur disponible : 128, qui correspond aux huit bits du champ d’exposant mis à 1. Dans ce cas, si les bits de la mantisse sont nuls alors le nombre représenté est plus ou moins l’infini. Sinon il s’agit de l’un des différents codes représentant un non numérique (les fameux NaN). Vous pouvez aller voir ici si cela vous intéresse.

Avant de conclure cet article, parlons un peu de précision pour les nombres normalisés. Comme on l’a vu plus tôt, la représentation flottante d’un nombre est une approximation de son logarithme en base deux. En simple précision, on a 23 digits après la virgule. Cela signifie que le plus petit incrément que l’on puisse réaliser sur un nombre représentable normalisé $x$ est $2^{−23} \times 2^{\lfloor log_2(x)\rfloor}$. Une conséquence assez directe, c’est que si $\lfloor log_2(x)\rfloor \geq 24$, alors le plus petit incrément est supérieur à 1! Ce qui donne une petite propriété intéressante des flottants :

julia > Float32(2^24) == Float32(2^24) + Float32(1)
true

C’est pourquoi choisir les flottants pour stocker des entiers pourrait avoir des conséquences imprévues ! Comme par exemple…

… dans Javascript qui utilise des flottants double précision (donc avec des mantisses de 52 bits après la virgule). Si par malheur quelqu’un voulait utiliser des entiers tels que $2^{53} = 9007199254740992$, iel pourrait faire face à des problèmes pour le moins peu évidents au premier regard.

>> var i = 9007199254740992;
undefined
>> i
9007199254740992
>> i + 1
9007199254740992
>> i + 2
9007199254740994