Dans le contexte de la statistique et en particulier de l’apprentissage automatique, la régularisation est le nom donné à un processus visant principalement à réduire des problèmes liés au surapprentissage. Et ce, au travers d’une réduction de la variance ou d’une sélection du nombre de paramètres employés. Ce processus n’est pas neutre puisqu’il consiste à introduire une nouvelle information au problème, dans l’objectif de le "simplifier", que ce soit en introduisant une pénalité d’autant plus grande que la complexité du modèle l’est ou en "imposant" une distribution a priori des paramètres du modèle.
Le principe général de la régularisation consiste à pénaliser les valeurs extrêmes des paramètres (ce qui conduit souvent à la variance du surapprentissage). On cherche alors à minimiser à la fois le modèle par rapport à notre métrique de choix ainsi qu’une métrique sur la taille et le nombre de paramètres employés.
Dans cet article, nous allons nous attarder sur une famille d’outils de régularisation liée aux modèles linéaires, nommément: ridge, lasso et elastic net. Mais il existe évidemment d’autres outils adaptés pour d’autres problématiques, nous pensons notamment aux AIC/BIC (Akaike information criterion/Bayesian information criterion), PCR (Principal component regression), PLS (Partial least squares), LARS (Least-angle regression), …
Ce billet fait l’hypothèse que vous ayez déjà une certaine compréhension de la manière dont fonctionnent les modèles linéaires, les concepts de biais et variance dans l’apprentissage automatique, ainsi que l’importance de la validation croisée dans ce domaine.
Méthode des moindres carrés
Tout d’abord, nous allons revenir sur la méthode des moindres carrés. Comme son nom l’indique, elle consiste à minimiser l’erreur entre les données réelles et prédites par le modèle. Supposons le jeu de données suivant contenant dix observations (numérotées de 1 à 10) et dont la mesure est proportionnelle à:
Nous obtenons le graphique suivant:
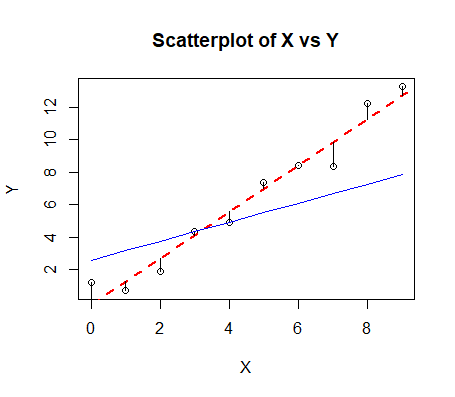
Une observation devrait sauter aux yeux sur ce graphique, en fonction de la population d’entraînement, on peut avoir une très grande différence au niveau des capacités prédictives du modèle, c’est ce qu’on appelle la variance liée au surapprentissage. Ici, la ligne en bleu est construite uniquement sur la base de deux points et non sur tous (comme en rouge).
D’autre part, on peut se demander comment l’erreur (des moindres carrés) évolue lorsque l’on fait varier le coefficient directeur (la pente) de la droite de régression mais sans modifier l’ordonnée à l’origine. Donc, en calculant: . On peut alors obtenir un graphique comme celui-ci:

Régularisation
Nous l’avons dit en introduction, le principe de la régularisation consiste à simplifier un modèle en cherchant souvent à pénaliser des valeurs extrêmes dans les paramètres ou en cherchant les paramètres expliquant au mieux les résultats obtenus, les plus explicatifs. Pour cela, on définit une métrique qui peut mesurer tant les valeurs des paramètres que leur nombre; et l’on préférera un modèle contenant "moins" de paramètres s’il parvient à des résultats similaires à un autre plus complexe.
Le processus consiste alors à minimiser deux expressions en même temps:
- La somme des résidus quadratiques liés au modèle en lui-même.
- Une expression combinant les coefficients du modèle.
Ridge regression
La régression qualifiée de "Ridge" consiste à minimiser la somme des carrées des coefficients, le tout pondéré par un facteur (noté ).
On se retrouve avec à minimiser l’expression suivante:
Somme des résidus quadratiques (RSS) + * (somme des carrés des coefficients - )
Ce paramètre est utilisé afin de pondérer plus ou moins l’importance de la minimisation du modèle en lui-même ou celle des coefficients.
- Lorsqu’il est égale à , on retombe sur le même résultat que la méthode des moindres carrés classique.
- Et lorsqu’il tend vers l’infini (), les coefficients vont tendre vers (mais sans jamais l’atteindre).
- Pour les valeurs intermédiaires, les coefficients vont être plus petits que dans le modèle non-régularisé.
- Et plus la valeur de augmente, au plus la complexité générale du modèle diminue.
Lasso regression
La régression qualifiée de "Lasso" consiste à minimiser la somme des valeurs absolues des coefficients, le tout pondéré par un facteur (noté ).
On se retrouve avec à minimiser l’expression suivante:
Somme des résidus quadratiques (RSS) + * (somme des valeurs absolues des coefficients - )
Les propriétés sont assez similaires entre la régression Ridge et Lasso, les différences fondamentales consistent en:
- Lorsque tend vers l’infini (), les coefficients vont tendre vers (mais sans jamais l’atteindre) dans le cadre de "Ridge" mais pourront atteindre pour "Lasso".
- "Ridge" est davantage adapté dans le cadre où les variables indépendantes sont fortement corrélées. Alors que "Lasso" permet de "sélectionner" les covariables en vue de rendre le modèle plus simple (vu que les coefficients peuvent devenir nuls).
- Vu que la norme est employée, cela a des répercussions sur les techniques d’optimisations possibles en vue de minimiser ce système.
Elastic net
La régularisation de type "Elastic net" consiste à combiner les deux régularisations précédentes (Ridge et Lasso) afin d’éviter la sélectivité trop forte que peut proposer Lasso tout en conservant possiblement des variables fortement corrélées.
Somme des résidus quadratiques (RSS) +
* (somme des valeurs absolues des coefficients - ) +
* (somme des carrés des coefficients - )
Dans les trois cas, le modèle est intrinsèquement changé, mais nous l’espérons pour un mieux ! Il reste néanmoins à trouver les valeurs pour les plus appropriées, et pour cela, la validation croisée peut s’avérer plus que nécessaire.
Mais dans le fond, quel est l’impact de ces régularisations sur notre problème:
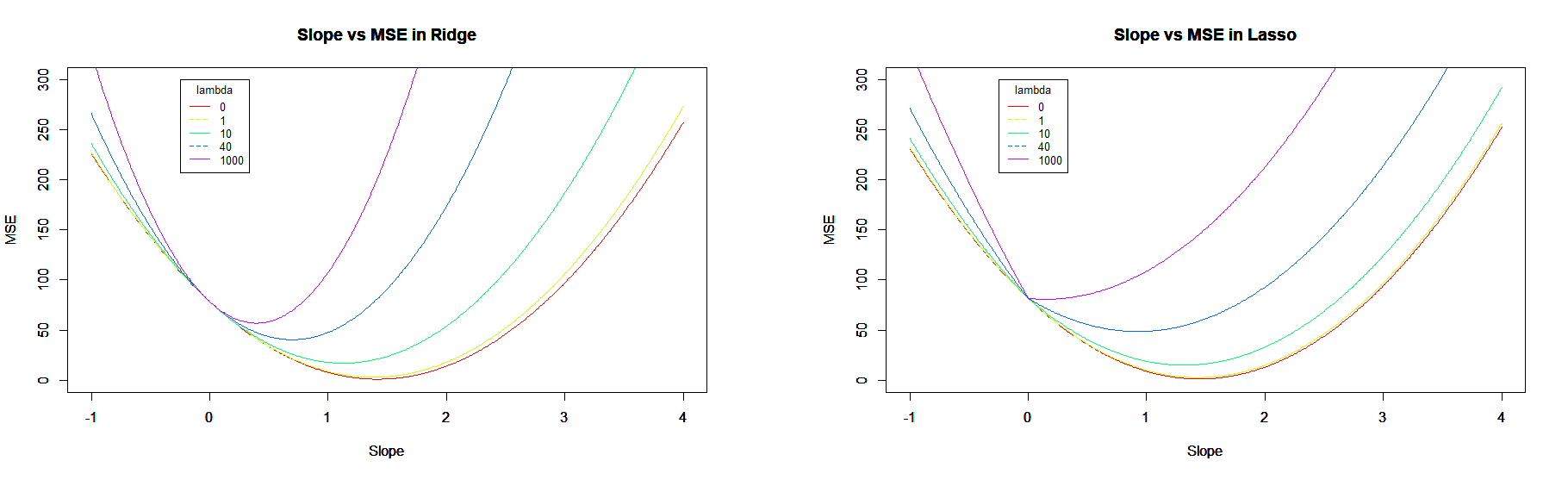
Naturellement, nous voyons l’erreur moyenne augmentée d’autant plus que le paramètre est grand. Mais nous comprenons également que l’erreur sera d’autant plus minimisée que la pente sera nulle. Dans le cadre de la régularisation de type Lasso, nous voyons de plus en plus fort une cassure de la courbe, liée à la norme .
Dans notre propos, nous n’avons évoqué que les modèles "linéaires" mais il est possible d’étendre les résultats, notamment aux variables discrètes (en considérant qu’on essaye de minimiser la distance entre toutes les observations liées à ces variables discrètes). Ainsi qu’aux régressions logistiques où l’on essaye de prédire une variable discrète en essayant d’optimiser le "maximum-likelihood".
L’un des grands avantages de la régularisation est lié à la facilité d’entraînement lorsqu’il n’y a pas assez de données. En effet, comment entraîner un modèle prédictif contenant des milliers de paramètres si nous ne possédons qu’une centaine d’exemples ? Il y a trop grande variabilité dans les résultats qui pourraient être obtenus et l’emploi du Lasso, par exemple, permettrait de facilement évincer tous les paramètres "inutiles" au modèle a priori.
On espère que ce billet aura su répondre aux questions que vous vous posiez sur ces notions, dans quels cas il est utile d’appliquer une régularisation. Quels sont les avantages et inconvénients d’une telle pratique sur les données et les hypothèses liées.