Lorsqu’on fait des mathématiques, on remarque souvent des liens entre 2 domaines de la matière. Dans ce billet nous allons voir un lien étonnant entre les nombre complexes et les matrices. Celui-ci est utile pour des langage qui ne gèrent que des matrices, par exemples.
Prérequis :
- Connaitre les nombres complexes
- Connaitre les matrices
Rappel sur les nombres complexes
Soit un nombre complexe , avec et . On dit que est la partie réelle de et la partie imaginaire.
Opérations sur les complexes
Soient ,
Rappel sur les matrices
Une matrice est un objet mathématique plusieurs nombres ordonnés en lignes et colonnes. Nous nous arrêterons dans ce billet aux matrices possédant 2 lignes et 2 colonnes.
Soient les matrices suivantes :
Opérations sur les matrices
On remarque qu’en général avec les matrices
Transfomer le complexe en matrice
L’astuce présentée ici, est assez simple.
Si on écrit un nombre complexe tel la matrice on retrouve les bonnes propriétés des complexes.
Ainsi :
On remarquera aussi que le déterminant de la matrice vaut le carré du module du complexe.
On a donc vu qu’un nombre complexe pouvait s’écrire comme une matrice particulère afin d’utiliser des complexes dans des langages qui ne gèrent que des matrices.
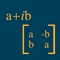





 ce qui permet de rendre la correspondance assez immédiate quand on connaît les deux
ce qui permet de rendre la correspondance assez immédiate quand on connaît les deux