Je m’attaque ici à l’exercice de spécialité. Le sujet peut-être trouvé ici.
Première partie
Première question
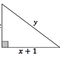
Tout d’abord, un triangle est rectangle si, et seulement si, il vérifie l’égalité de Pythagore. Donc un couple d’entiers $(x,y)$ définit un triangle TRPI si, et seulement si, :
Deuxième question
On essaye successivement $x=1,x=2$ et $x=3$. Les deux premiers donnent $y^2 = 3$ et $y^2 = 13$ qui ne sont pas des carrés (ce sont des nombres premiers). Le dernier donne $y^2 = 25$ et $y=5$ est solution.
Le couple $(3,5)$ est donc bien minimal.
Troisième question
Petit a
C’est un grand classique à connaître absolument.
Si $n$ est impair, alors $n=2k+1$ avec $k$ entier et donc :
est impair (car $2k^2+2k$ est entier).
Maintenant, si $n$ est pair avec $n=2k$ alors $n^2 = 4k^2$ est pair.
Finalement, si $n^2$ est impair alors $n$ est nécessairement impair (car sinon $n^2$ serait pair). De même, si $n^2$ est pair alors $n$ est nécessairement pair.
Petit b
Si $x$ est pair alors $x+1$ est impair et si $x$ est impair alors $x+1$ est pair.
De sorte que, quelque soit la parité de $x$, $x^2+ (x+1)^2$ est la somme d’un nombre pair et impair. Donc c’est un nombre impair. Donc $y^2$ est un nombre impair et donc $y$ également.
Quatrième question
Par l’absurde, supposons que $p\neq 1$ divise $x$ et $y$. Alors on pose $y= pk$ et $x = pn$. Il vient
or $p$ ne divise pas $1$ et donc ne peut pas diviser $p(2n^2+2n)+1$. Pourtant il divise $y^2$, absurde, donc $x$ et $y$ sont premiers entre eux.
Deuxième partie
Première question
On fait le produit :
et en sommant avec $B$ on obtient :
Deuxième question
Petit a
On calcule :
comme annoncé.
Petit b
Le couple $(x,y)$ définit un triangle TRPI si, et seulement si,
or
et donc $(y',x')$ définit un triangle TRPI si $(x,y)$ en définit un.
Troisième question
Comme $(x_0,y_0) = (3,5)$, on sait que ce couple définit un triangle TRPI du fait de la deuxième question de la partie B.
On remarque maintenant que la question précédente montre que si $(x_n,y_n)$ définit un triangle TRPI alors $(x_{n+1},y_{n+1}) = (x_n',y_n')$ aussi.
Par principe de récurrence, on conclut.
Quatrième question
La question précédente donne une façon de trouver un tel $x\geq 2017$. En effet, on peut calculer successivement les couples $(x_n,y_n)$ en prenant $(x_0,y_0) = (3,5)$ et en utilisant l’identité :
On peut donc utiliser l’algorithme suivant :
1 2 3 4 5 6 7 8 9 10 | X=3
Y=5
Tant que X<2017 :
A = X
X = 3X + 2Y + 1
Y = 4A + 3Y + 2
FinTantQue
Afficher (X,Y)
|
(Cet algorithme termine nécessairement du fait de la croissance linéaire du couple $(x_n,y_n)$.)
On obtient avec cet algorithme le résultat :
Chouette exercice !
Par contre si je ne me trompe pas, lorsque tu prouve que si 
Donc je pense qu’il faut le montrer dans l’autre sens : si 
)
